De-biased Machine Learning for Compliers

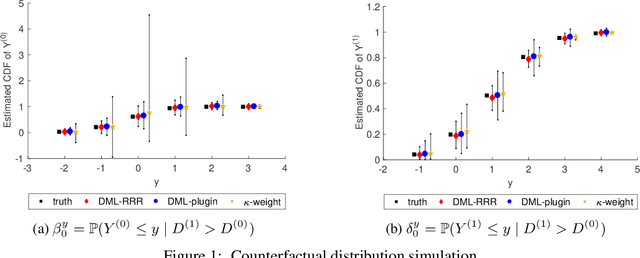
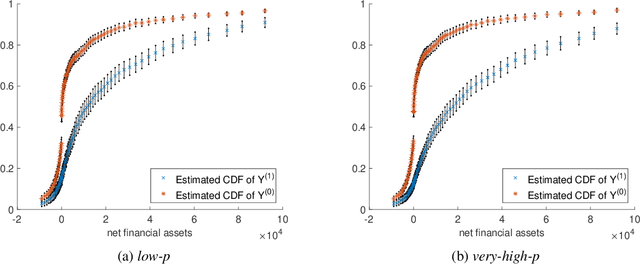
Instrumental variable identification is a concept in causal statistics for estimating the counterfactual effect of treatment D on output Y controlling for covariates X using observational data. Even when measurements of (Y,D) are confounded, the treatment effect on the subpopulation of compliers can nonetheless be identified if an instrumental variable Z is available, which is independent of (Y,D) conditional on X and the unmeasured confounder. We introduce a de-biased machine learning (DML) approach to estimating complier parameters with high-dimensional data. Complier parameters include local average treatment effect, average complier characteristics, and complier counterfactual outcome distributions. In our approach, the de-biasing is itself performed by machine learning, a variant called de-biased machine learning via regularized Riesz representers (DML-RRR). We prove our estimator is consistent, asymptotically normal, and semi-parametrically efficient. In experiments, our estimator outperforms state of the art alternatives. We use it to estimate the effect of 401(k) participation on the distribution of net financial assets.

Kernel Instrumental Variable Regression

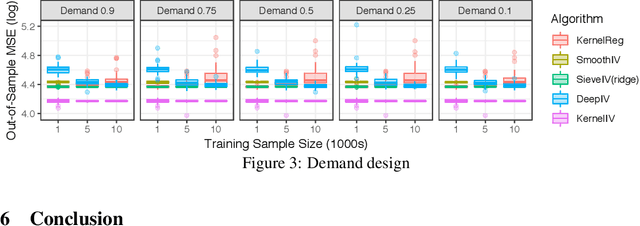
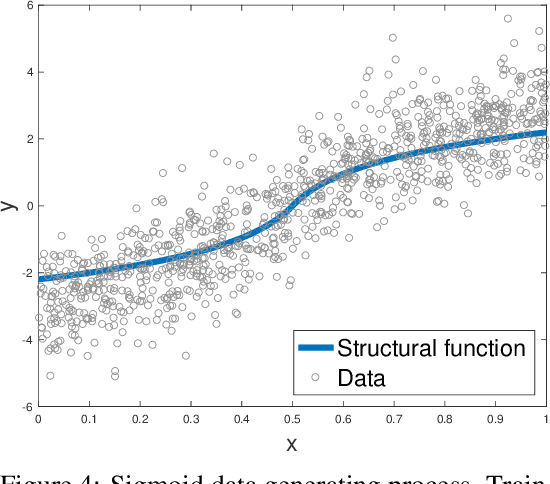
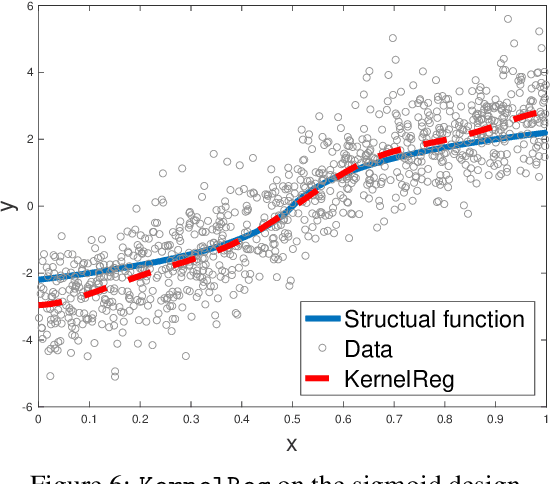
Instrumental variable regression is a strategy for learning causal relationships in observational data. If measurements of input X and output Y are confounded, the causal relationship can nonetheless be identified if an instrumental variable Z is available that influences X directly, but is conditionally independent of Y given X. The classic two-stage least squares algorithm (2SLS) simplifies the estimation problem by modeling all relationships as linear functions. We propose kernel instrumental variable regression (KIV), a nonparametric generalization of 2SLS, modeling relations among X, Y, and Z as nonlinear functions in reproducing kernel Hilbert spaces (RKHSs). We prove the consistency of KIV under mild assumptions, and derive conditions under which the convergence rate achieves the minimax optimal rate for unconfounded, one-stage RKHS regression. In doing so, we obtain an efficient ratio between training sample sizes used in the algorithm's first and second stages. In experiments, KIV outperforms state of the art alternatives for nonparametric instrumental variable regression.

3D Deep Learning with voxelized atomic configurations for modeling atomistic potentials in complex solid-solution alloys

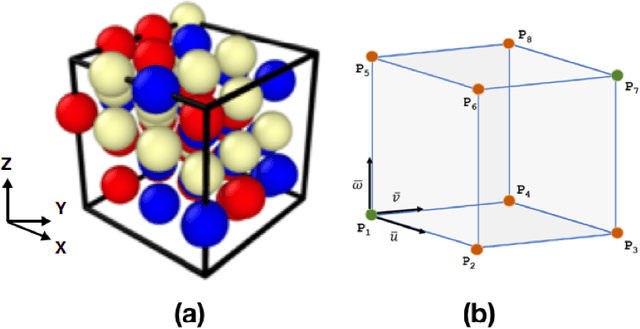
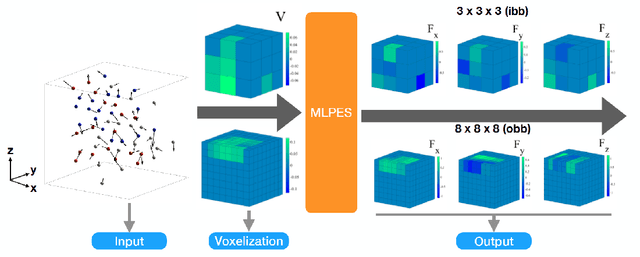
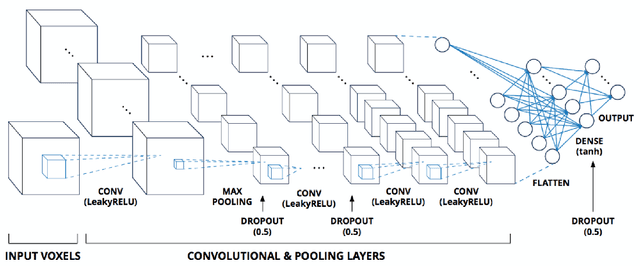
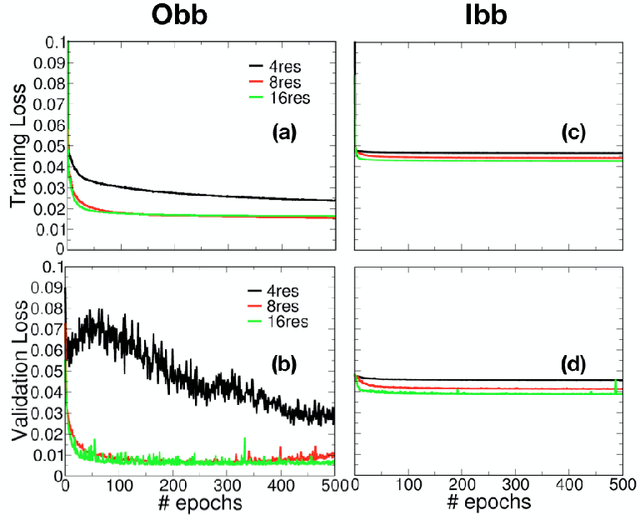
The need for advanced materials has led to the development of complex, multi-component alloys or solid-solution alloys. These materials have shown exceptional properties like strength, toughness, ductility, electrical and electronic properties. Current development of such material systems are hindered by expensive experiments and computationally demanding first-principles simulations. Atomistic simulations can provide reasonable insights on properties in such material systems. However, the issue of designing robust potentials still exists. In this paper, we explore a deep convolutional neural-network based approach to develop the atomistic potential for such complex alloys to investigate materials for insights into controlling properties. In the present work, we propose a voxel representation of the atomic configuration of a cell and design a 3D convolutional neural network to learn the interaction of the atoms. Our results highlight the performance of the 3D convolutional neural network and its efficacy in machine-learning the atomistic potential. We also explore the role of voxel resolution and provide insights into the two bounding box methodologies implemented for voxelization.

Physics-aware Deep Generative Models for Creating Synthetic Microstructures

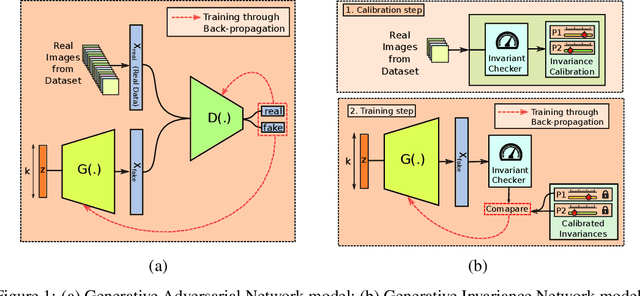
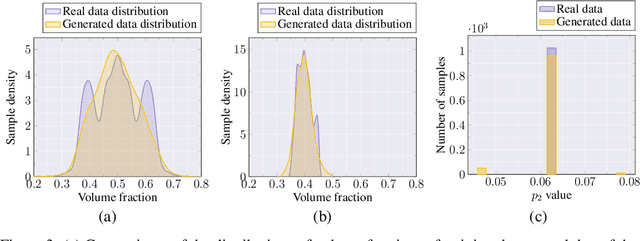
A key problem in computational material science deals with understanding the effect of material distribution (i.e., microstructure) on material performance. The challenge is to synthesize microstructures, given a finite number of microstructure images, and/or some physical invariances that the microstructure exhibits. Conventional approaches are based on stochastic optimization and are computationally intensive. We introduce three generative models for the fast synthesis of binary microstructure images. The first model is a WGAN model that uses a finite number of training images to synthesize new microstructures that weakly satisfy the physical invariances respected by the original data. The second model explicitly enforces known physical invariances by replacing the traditional discriminator in a GAN with an invariance checker. Our third model combines the first two models to reconstruct microstructures that respect both explicit physics invariances as well as implicit constraints learned from the image data. We illustrate these models by reconstructing two-phase microstructures that exhibit coarsening behavior. The trained models also exhibit interesting latent variable interpolation behavior, and the results indicate considerable promise for enforcing user-defined physics constraints during microstructure synthesis.

Throughput Optimal Decentralized Scheduling of Multi-Hop Networks with End-to-End Deadline Constraints: II Wireless Networks with Interference

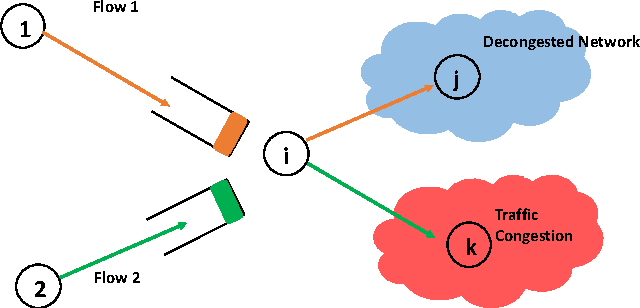
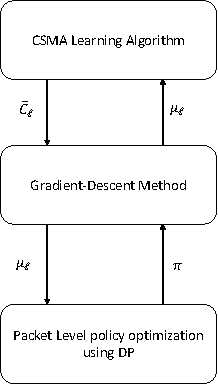
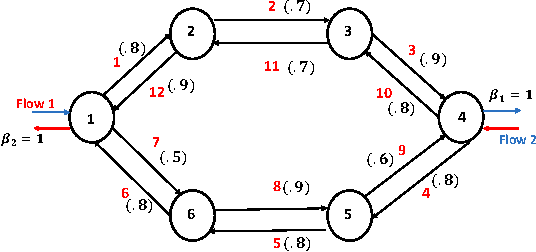
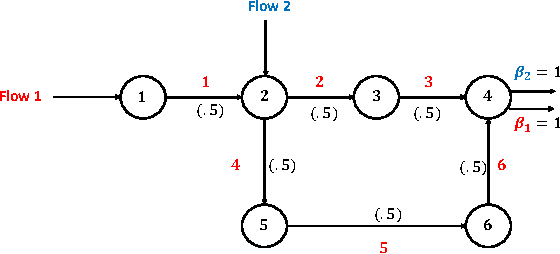
Consider a multihop wireless network serving multiple flows in which wireless link interference constraints are described by a link interference graph. For such a network, we design routing-scheduling policies that maximize the end-to-end timely throughput of the network. Timely throughput of a flow $f$ is defined as the average rate at which packets of flow $f$ reach their destination node $d_f$ within their deadline. Our policy has several surprising characteristics. Firstly, we show that the optimal routing-scheduling decision for an individual packet that is present at a wireless node $i\in V$ is solely a function of its location, and "age". Thus, a wireless node $i$ does not require the knowledge of the "global" network state in order to maximize the timely throughput. We notice that in comparison, under the backpressure routing policy, a node $i$ requires only the knowledge of its neighbours queue lengths in order to guarantee maximal stability, and hence is decentralized. The key difference arises due to the fact that in our set-up the packets loose their utility once their "age" has crossed their deadline, thus making the task of optimizing timely throughput much more challenging than that of ensuring network stability. Of course, due to this key difference, the decision process involved in maximizing the timely throughput is also much more complex than that involved in ensuring network-wide queue stabilization. In view of this, our results are somewhat surprising.

Kiefer Wolfowitz Algorithm is Asymptotically Optimal for a Class of Non-Stationary Bandit Problems

We consider the problem of designing an allocation rule or an "online learning algorithm" for a class of bandit problems in which the set of control actions available at each time $s$ is a convex, compact subset of $\mathbb{R}^d$. Upon choosing an action $x$ at time $s$, the algorithm obtains a noisy value of the unknown and time-varying function $f_s$ evaluated at $x$. The "regret" of an algorithm is the gap between its expected reward, and the reward earned by a strategy which has the knowledge of the function $f_s$ at each time $s$ and hence chooses the action $x_s$ that maximizes $f_s$. For this non-stationary bandit problem set-up, we consider two variants of the Kiefer Wolfowitz (KW) algorithm i) KW with fixed step-size $\beta$, and ii) KW with sliding window of length $L$. We show that if the number of times that the function $f_s$ varies during time $T$ is $o(T)$, and if the learning rates of the proposed algorithms are chosen "optimally", then the regret of the proposed algorithms is $o(T)$, and hence the algorithms are asymptotically efficient.