On the Infinite Width and Depth Limits of Predictive Coding Networks

Predictive coding (PC) is a biologically plausible alternative to standard backpropagation (BP) that minimises an energy function with respect to network activities before updating weights. Recent work has improved the training stability of deep PC networks (PCNs) by leveraging some BP-inspired reparameterisations. However, the full scalability and theoretical basis of these approaches remains unclear. To address this, we study the infinite width and depth limits of PCNs. For linear residual networks, we show that the set of width- and depth-stable feature-learning parameterisations for PC is exactly the same as for BP. Moreover, under any of these parameterisations, the PC energy with equilibrated activities converges to the BP loss in a regime where the model width is much larger than the depth, resulting in PC computing the same gradients as BP. Experiments show that these results hold in practice for deep nonlinear networks, as long as an activity equilibrium seem to be reached. Overall, this work unifies various previous theoretical and empirical results and has potentially important implications for the scaling of PCNs.

Bidirectional predictive coding

Predictive coding (PC) is an influential computational model of visual learning and inference in the brain. Classical PC was proposed as a top-down generative model, where the brain actively predicts upcoming visual inputs, and inference minimises the prediction errors. Recent studies have also shown that PC can be formulated as a discriminative model, where sensory inputs predict neural activities in a feedforward manner. However, experimental evidence suggests that the brain employs both generative and discriminative inference, while unidirectional PC models show degraded performance in tasks requiring bidirectional processing. In this work, we propose bidirectional PC (bPC), a PC model that incorporates both generative and discriminative inference while maintaining a biologically plausible circuit implementation. We show that bPC matches or outperforms unidirectional models in their specialised generative or discriminative tasks, by developing an energy landscape that simultaneously suits both tasks. We also demonstrate bPC's superior performance in two biologically relevant tasks including multimodal learning and inference with missing information, suggesting that bPC resembles biological visual inference more closely.

Error Optimization: Overcoming Exponential Signal Decay in Deep Predictive Coding Networks

Predictive Coding (PC) offers a biologically plausible alternative to backpropagation for neural network training, yet struggles with deeper architectures. This paper identifies the root cause: an inherent signal decay problem where gradients attenuate exponentially with depth, becoming computationally negligible due to numerical precision constraints. To address this fundamental limitation, we introduce Error Optimization (EO), a novel reparameterization that preserves PC's theoretical properties while eliminating signal decay. By optimizing over prediction errors rather than states, EO enables signals to reach all layers simultaneously and without attenuation, converging orders of magnitude faster than standard PC. Experiments across multiple architectures and datasets demonstrate that EO matches backpropagation's performance even for deeper models where conventional PC struggles. Besides practical improvements, our work provides theoretical insight into PC dynamics and establishes a foundation for scaling biologically-inspired learning to deeper architectures on digital hardware and beyond.

Benchmarking Predictive Coding Networks -- Made Simple

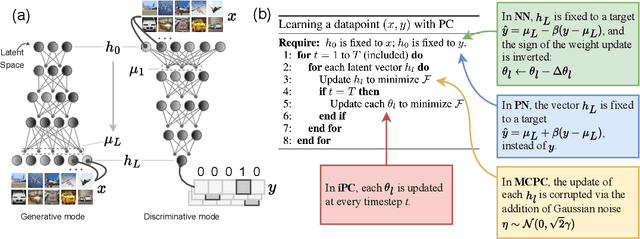
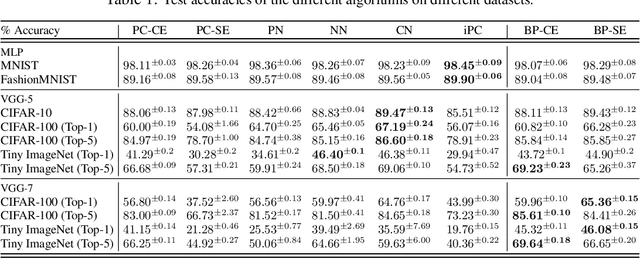
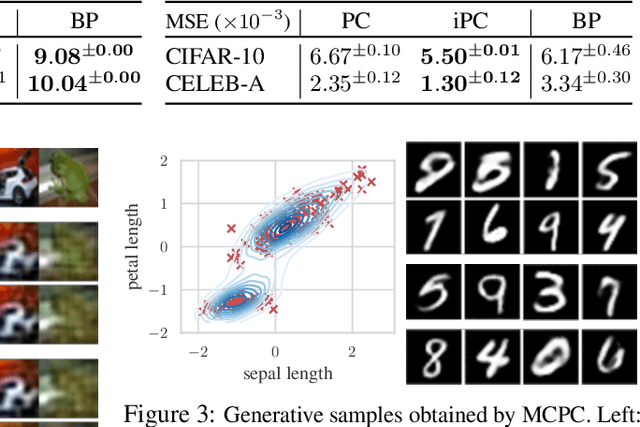
In this work, we tackle the problems of efficiency and scalability for predictive coding networks in machine learning. To do so, we first propose a library called PCX, whose focus lies on performance and simplicity, and provides a user-friendly, deep-learning oriented interface. Second, we use PCX to implement a large set of benchmarks for the community to use for their experiments. As most works propose their own tasks and architectures, do not compare one against each other, and focus on small-scale tasks, a simple and fast open-source library adopted by the whole community would address all of these concerns. Third, we perform extensive benchmarks using multiple algorithms, setting new state-of-the-art results in multiple tasks and datasets, as well as highlighting limitations inherent to PC that should be addressed. Thanks to the efficiency of PCX, we are able to analyze larger architectures than commonly used, providing baselines to galvanize community efforts towards one of the main open problems in the field: scalability. The code for PCX is available at \textit{https://github.com/liukidar/pcax}.

Associative Memories in the Feature Space

An autoassociative memory model is a function that, given a set of data points, takes as input an arbitrary vector and outputs the most similar data point from the memorized set. However, popular memory models fail to retrieve images even when the corruption is mild and easy to detect for a human evaluator. This is because similarities are evaluated in the raw pixel space, which does not contain any semantic information about the images. This problem can be easily solved by computing \emph{similarities} in an embedding space instead of the pixel space. We show that an effective way of computing such embeddings is via a network pretrained with a contrastive loss. As the dimension of embedding spaces is often significantly smaller than the pixel space, we also have a faster computation of similarity scores. We test this method on complex datasets such as CIFAR10 and STL10. An additional drawback of current models is the need of storing the whole dataset in the pixel space, which is often extremely large. We relax this condition and propose a class of memory models that only stores low-dimensional semantic embeddings, and uses them to retrieve similar, but not identical, memories. We demonstrate a proof of concept of this method on a simple task on the MNIST dataset.

Sequential Memory with Temporal Predictive Coding

Memorizing the temporal order of event sequences is critical for the survival of biological agents. However, the computational mechanism underlying sequential memory in the brain remains unclear. Inspired by neuroscience theories and recent successes in applying predictive coding (PC) to static memory tasks, in this work we propose a novel PC-based model for sequential memory, called temporal predictive coding (tPC). We show that our tPC models can memorize and retrieve sequential inputs accurately with a biologically plausible neural implementation. Importantly, our analytical study reveals that tPC can be viewed as a classical Asymmetric Hopfield Network (AHN) with an implicit statistical whitening process, which leads to more stable performance in sequential memory tasks of structured inputs. Moreover, we find that tPC with a multi-layer structure can encode context-dependent information, thus distinguishing between repeating elements appearing in a sequence, a computation attributed to the hippocampus. Our work establishes a possible computational mechanism underlying sequential memory in the brain that can also be theoretically interpreted using existing memory model frameworks.

Incremental Predictive Coding: A Parallel and Fully Automatic Learning Algorithm

Neuroscience-inspired models, such as predictive coding, have the potential to play an important role in the future of machine intelligence. However, they are not yet used in industrial applications due to some limitations, such as the lack of efficiency. In this work, we address this by proposing incremental predictive coding (iPC), a variation of the original framework derived from the incremental expectation maximization algorithm, where every operation can be performed in parallel without external control. We show both theoretically and empirically that iPC is much faster than the original algorithm originally developed by Rao and Ballard, while maintaining performance comparable to backpropagation in image classification tasks. This work impacts several areas, has general applications in computational neuroscience and machine learning, and specific applications in scenarios where automatization and parallelization are important, such as distributed computing and implementations of deep learning models on analog and neuromorphic chips.

A Theoretical Framework for Inference and Learning in Predictive Coding Networks

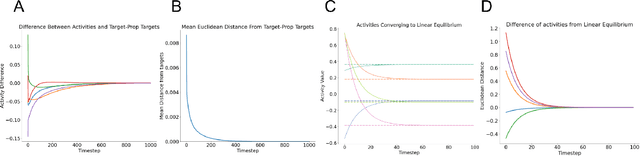
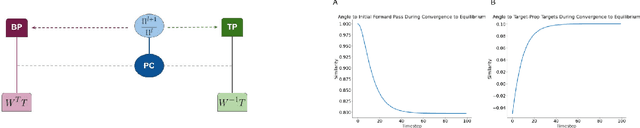
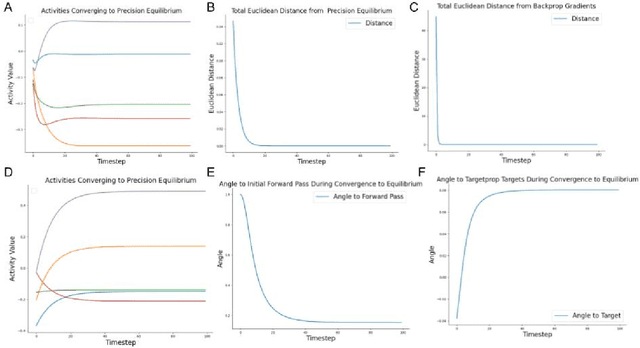
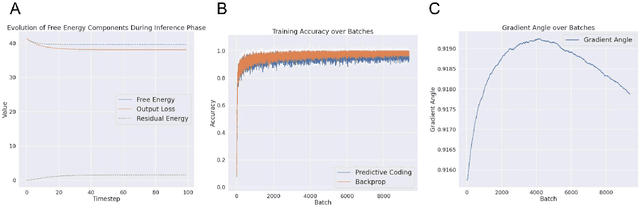
Predictive coding (PC) is an influential theory in computational neuroscience, which argues that the cortex forms unsupervised world models by implementing a hierarchical process of prediction error minimization. PC networks (PCNs) are trained in two phases. First, neural activities are updated to optimize the network's response to external stimuli. Second, synaptic weights are updated to consolidate this change in activity -- an algorithm called \emph{prospective configuration}. While previous work has shown how in various limits, PCNs can be found to approximate backpropagation (BP), recent work has demonstrated that PCNs operating in this standard regime, which does not approximate BP, nevertheless obtain competitive training and generalization performance to BP-trained networks while outperforming them on tasks such as online, few-shot, and continual learning, where brains are known to excel. Despite this promising empirical performance, little is understood theoretically about the properties and dynamics of PCNs in this regime. In this paper, we provide a comprehensive theoretical analysis of the properties of PCNs trained with prospective configuration. We first derive analytical results concerning the inference equilibrium for PCNs and a previously unknown close connection relationship to target propagation (TP). Secondly, we provide a theoretical analysis of learning in PCNs as a variant of generalized expectation-maximization and use that to prove the convergence of PCNs to critical points of the BP loss function, thus showing that deep PCNs can, in theory, achieve the same generalization performance as BP, while maintaining their unique advantages.

Backpropagation at the Infinitesimal Inference Limit of Energy-Based Models: Unifying Predictive Coding, Equilibrium Propagation, and Contrastive Hebbian Learning

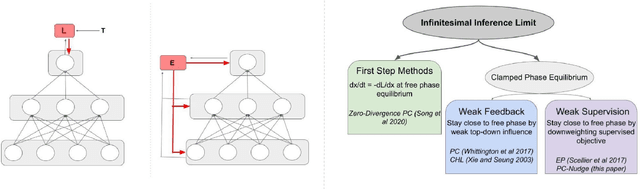
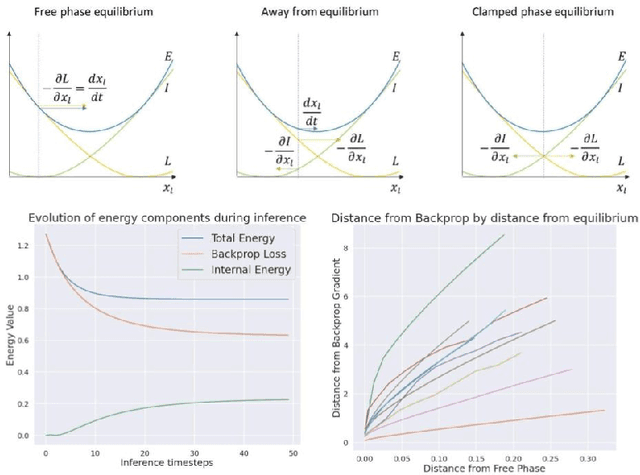
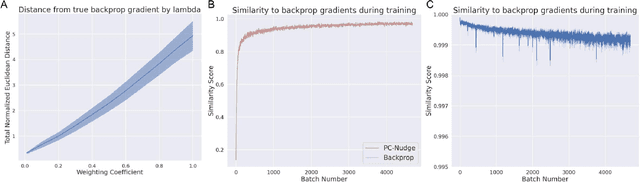
How the brain performs credit assignment is a fundamental unsolved problem in neuroscience. Many `biologically plausible' algorithms have been proposed, which compute gradients that approximate those computed by backpropagation (BP), and which operate in ways that more closely satisfy the constraints imposed by neural circuitry. Many such algorithms utilize the framework of energy-based models (EBMs), in which all free variables in the model are optimized to minimize a global energy function. However, in the literature, these algorithms exist in isolation and no unified theory exists linking them together. Here, we provide a comprehensive theory of the conditions under which EBMs can approximate BP, which lets us unify many of the BP approximation results in the literature (namely, predictive coding, equilibrium propagation, and contrastive Hebbian learning) and demonstrate that their approximation to BP arises from a simple and general mathematical property of EBMs at free-phase equilibrium. This property can then be exploited in different ways with different energy functions, and these specific choices yield a family of BP-approximating algorithms, which both includes the known results in the literature and can be used to derive new ones.

Predictive Coding: Towards a Future of Deep Learning beyond Backpropagation?

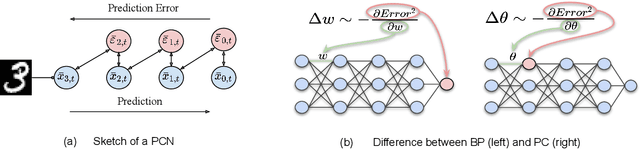
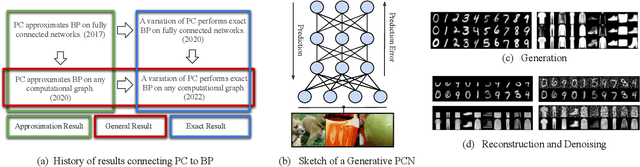
The backpropagation of error algorithm used to train deep neural networks has been fundamental to the successes of deep learning. However, it requires sequential backward updates and non-local computations, which make it challenging to parallelize at scale and is unlike how learning works in the brain. Neuroscience-inspired learning algorithms, however, such as \emph{predictive coding}, which utilize local learning, have the potential to overcome these limitations and advance beyond current deep learning technologies. While predictive coding originated in theoretical neuroscience as a model of information processing in the cortex, recent work has developed the idea into a general-purpose algorithm able to train neural networks using only local computations. In this survey, we review works that have contributed to this perspective and demonstrate the close theoretical connections between predictive coding and backpropagation, as well as works that highlight the multiple advantages of using predictive coding models over backpropagation-trained neural networks. Specifically, we show the substantially greater flexibility of predictive coding networks against equivalent deep neural networks, which can function as classifiers, generators, and associative memories simultaneously, and can be defined on arbitrary graph topologies. Finally, we review direct benchmarks of predictive coding networks on machine learning classification tasks, as well as its close connections to control theory and applications in robotics.