Distribution-Dependent Rates for Multi-Distribution Learning

To address the needs of modeling uncertainty in sensitive machine learning applications, the setup of distributionally robust optimization (DRO) seeks good performance uniformly across a variety of tasks. The recent multi-distribution learning (MDL) framework tackles this objective in a dynamic interaction with the environment, where the learner has sampling access to each target distribution. Drawing inspiration from the field of pure-exploration multi-armed bandits, we provide distribution-dependent guarantees in the MDL regime, that scale with suboptimality gaps and result in superior dependence on the sample size when compared to the existing distribution-independent analyses. We investigate two non-adaptive strategies, uniform and non-uniform exploration, and present non-asymptotic regret bounds using novel tools from empirical process theory. Furthermore, we devise an adaptive optimistic algorithm, LCB-DR, that showcases enhanced dependence on the gaps, mirroring the contrast between uniform and optimistic allocation in the multi-armed bandit literature.

On Accelerated Perceptrons and Beyond

The classical Perceptron algorithm of Rosenblatt can be used to find a linear threshold function to correctly classify $n$ linearly separable data points, assuming the classes are separated by some margin $\gamma > 0$. A foundational result is that Perceptron converges after $\Omega(1/\gamma^{2})$ iterations. There have been several recent works that managed to improve this rate by a quadratic factor, to $\Omega(\sqrt{\log n}/\gamma)$, with more sophisticated algorithms. In this paper, we unify these existing results under one framework by showing that they can all be described through the lens of solving min-max problems using modern acceleration techniques, mainly through optimistic online learning. We then show that the proposed framework also lead to improved results for a series of problems beyond the standard Perceptron setting. Specifically, a) For the margin maximization problem, we improve the state-of-the-art result from $O(\log t/t^2)$ to $O(1/t^2)$, where $t$ is the number of iterations; b) We provide the first result on identifying the implicit bias property of the classical Nesterov's accelerated gradient descent (NAG) algorithm, and show NAG can maximize the margin with an $O(1/t^2)$ rate; c) For the classical $p$-norm Perceptron problem, we provide an algorithm with $\Omega(\sqrt{(p-1)\log n}/\gamma)$ convergence rate, while existing algorithms suffer the $\Omega({(p-1)}/\gamma^2)$ convergence rate.

Linear Separation via Optimism

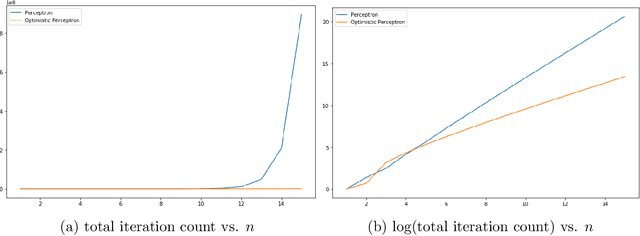
Binary linear classification has been explored since the very early days of the machine learning literature. Perhaps the most classical algorithm is the Perceptron, where a weight vector used to classify examples is maintained, and additive updates are made as incorrect examples are discovered. The Perceptron has been thoroughly studied and several versions have been proposed over many decades. The key theoretical fact about the Perceptron is that, so long as a perfect linear classifier exists with some margin $\gamma > 0$, the number of required updates to find such a perfect linear separator is bounded by $\frac{1}{\gamma^2}$. What has never been fully addressed is: does there exist an algorithm that can achieve this with fewer updates? In this paper we answer this in the affirmative: we propose the Optimistic Perceptron algorithm, a simple procedure that finds a separating hyperplane in no more than $\frac{1}{\gamma}$ updates. We also show experimentally that this procedure can significantly outperform Perceptron.