Linear Separation via Optimism
Paper and Code
Nov 17, 2020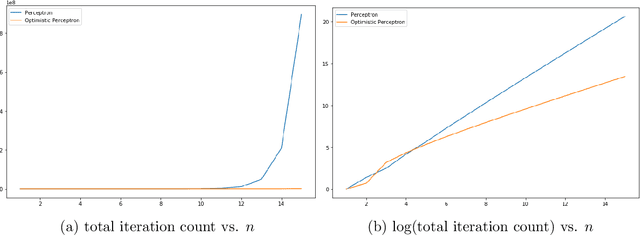
Binary linear classification has been explored since the very early days of the machine learning literature. Perhaps the most classical algorithm is the Perceptron, where a weight vector used to classify examples is maintained, and additive updates are made as incorrect examples are discovered. The Perceptron has been thoroughly studied and several versions have been proposed over many decades. The key theoretical fact about the Perceptron is that, so long as a perfect linear classifier exists with some margin $\gamma > 0$, the number of required updates to find such a perfect linear separator is bounded by $\frac{1}{\gamma^2}$. What has never been fully addressed is: does there exist an algorithm that can achieve this with fewer updates? In this paper we answer this in the affirmative: we propose the Optimistic Perceptron algorithm, a simple procedure that finds a separating hyperplane in no more than $\frac{1}{\gamma}$ updates. We also show experimentally that this procedure can significantly outperform Perceptron.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge