A Unified Convergence Analysis for Shuffling-Type Gradient Methods

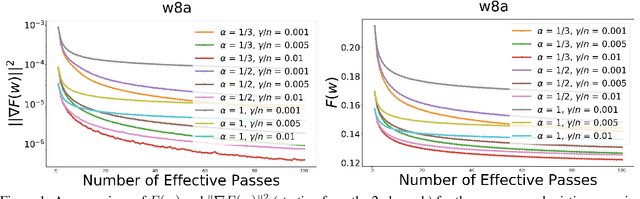
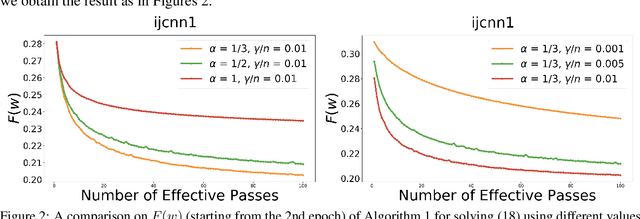
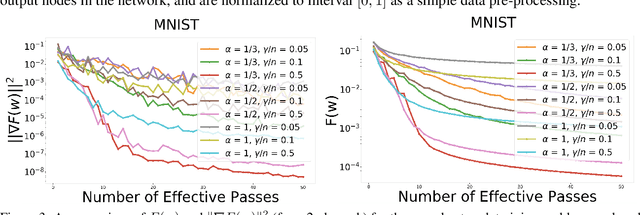
In this paper, we provide a unified convergence analysis for a class of shuffling-type gradient methods for solving a well-known finite-sum minimization problem commonly used in machine learning. This algorithm covers various variants such as randomized reshuffling, single shuffling, and cyclic/incremental gradient schemes. We consider two different settings: strongly convex and non-convex problems. Our main contribution consists of new non-asymptotic and asymptotic convergence rates for a general class of shuffling-type gradient methods to solve both non-convex and strongly convex problems. While our rate in the non-convex problem is new (i.e. not known yet under standard assumptions), the rate on the strongly convex case matches (up to a constant) the best-known results. However, unlike existing works in this direction, we only use standard assumptions such as smoothness and strong convexity. Finally, we empirically illustrate the effect of learning rates via a non-convex logistic regression and neural network examples.

Stochastic Gauss-Newton Algorithms for Nonconvex Compositional Optimization

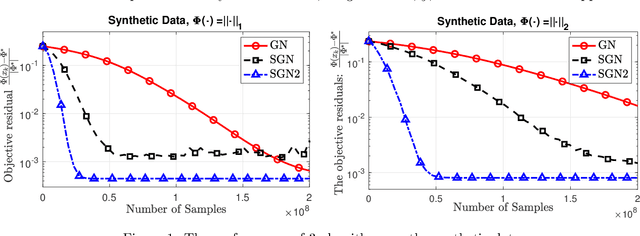
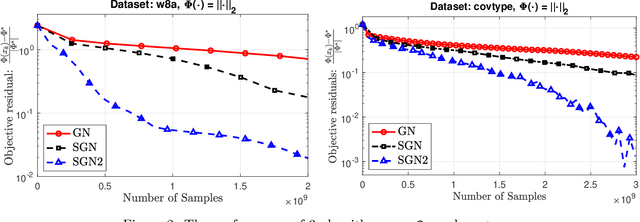
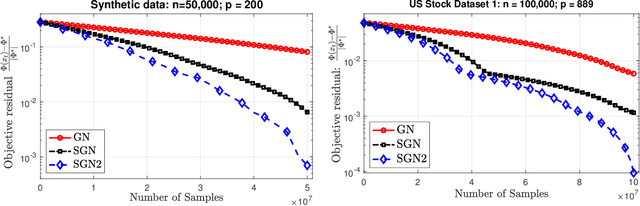
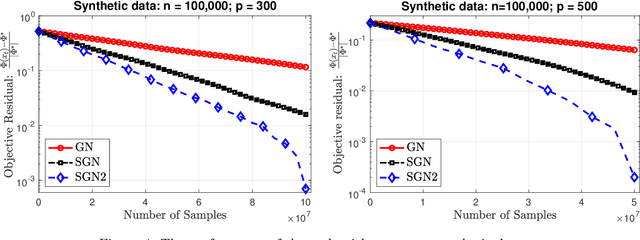
We develop two new stochastic Gauss-Newton algorithms for solving a class of stochastic nonconvex compositional optimization problems frequently arising in practice. We consider both the expectation and finite-sum settings under standard assumptions. We use both classical stochastic and SARAH estimators for approximating function values and Jacobians. In the expectation case, we establish $\mathcal{O}(\varepsilon^{-2})$ iteration complexity to achieve a stationary point in expectation and estimate the total number of stochastic oracle calls for both function values and its Jacobian, where $\varepsilon$ is a desired accuracy. In the finite sum case, we also estimate the same iteration complexity and the total oracle calls with high probability. To our best knowledge, this is the first time such global stochastic oracle complexity is established for stochastic Gauss-Newton methods. We illustrate our theoretical results via numerical examples on both synthetic and real datasets.

A Newton Frank-Wolfe Method for Constrained Self-Concordant Minimization

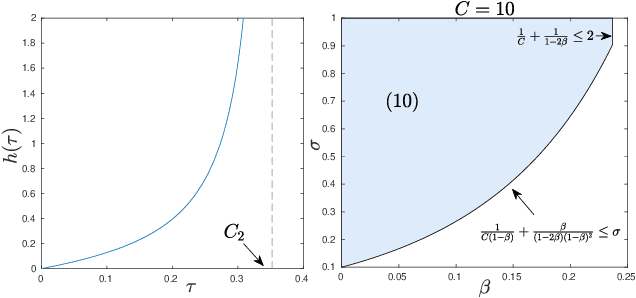
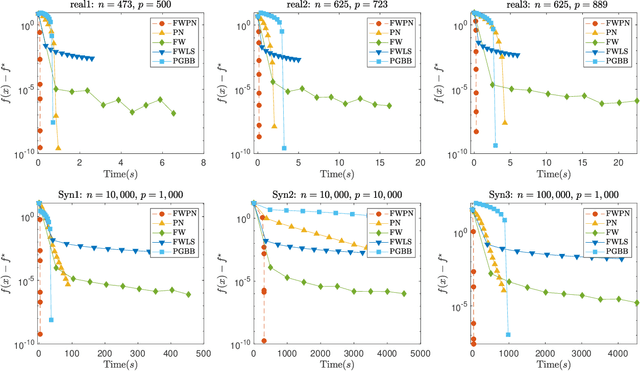
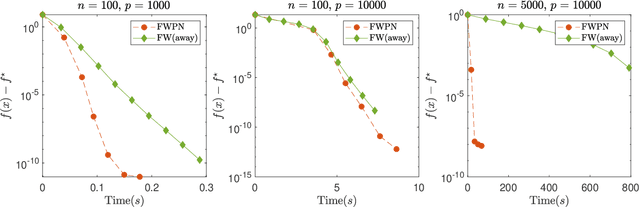
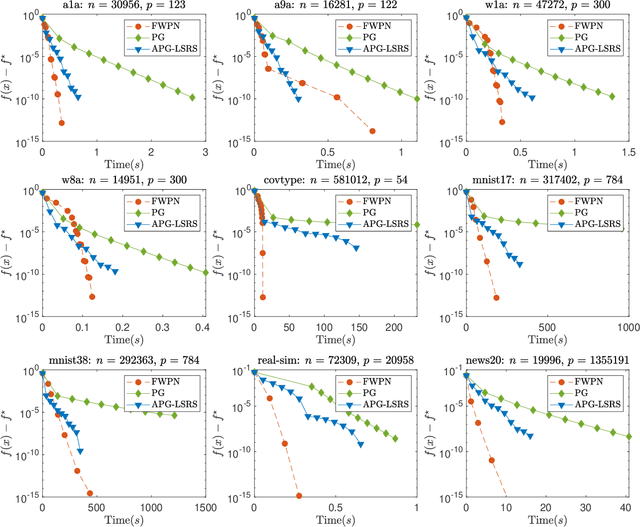
We demonstrate how to scalably solve a class of constrained self-concordant minimization problems using linear minimization oracles (LMO) over the constraint set. We prove that the number of LMO calls of our method is nearly the same as that of the Frank-Wolfe method in the L-smooth case. Specifically, our Newton Frank-Wolfe method uses $\mathcal{O}(\epsilon^{-\nu})$ LMO's, where $\epsilon$ is the desired accuracy and $\nu:= 1 + o(1)$. In addition, we demonstrate how our algorithm can exploit the improved variants of the LMO-based schemes, including away-steps, to attain linear convergence rates. We also provide numerical evidence with portfolio design with the competitive ratio, D-optimal experimental design, and logistic regression with the elastic net where Newton Frank-Wolfe outperforms the state-of-the-art.

Using positive spanning sets to achieve stationarity with the Boosted DC Algorithm

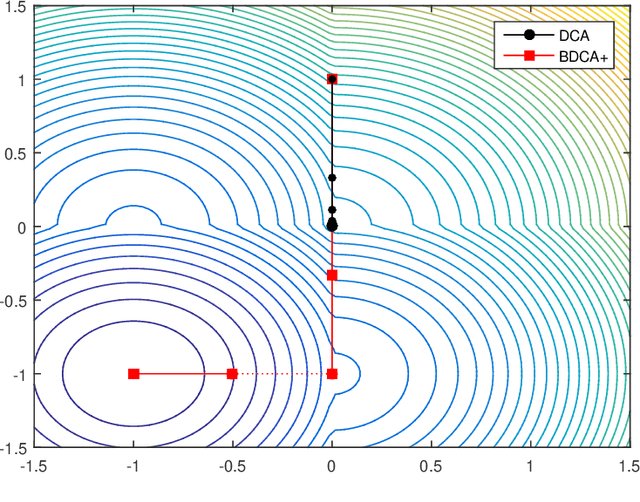
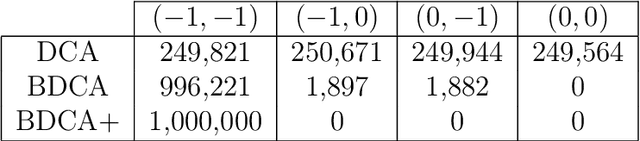
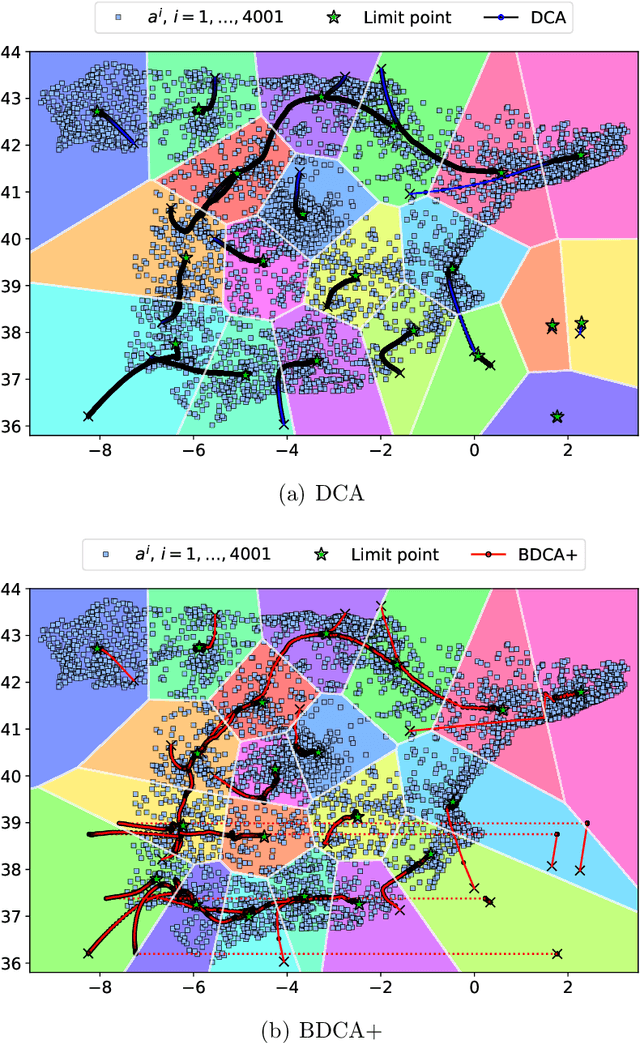
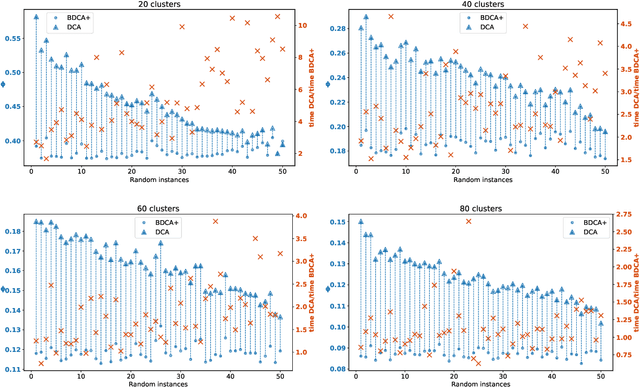
The Difference of Convex function Algorithm (DCA) is widely used for minimizing the difference of two convex functions. A recently proposed accelerated version, termed BDCA for Boosted DC Algorithm, incorporates a line search step to achieve a larger decrease of the objective value at each iteration. Thanks to this step, BDCA usually converges much faster than DCA in practice. The solutions found by DCA are guaranteed to be critical points of the problem, but they are rarely local minima. Although BDCA tends to improve the objective value of the solutions it finds, these are frequently just critical points as well. In this paper we combine BDCA with a simple Derivative-Free Optimization (DFO) algorithm to force the stationarity (lack of descent direction) at the point obtained. The potential of this approach is illustrated through some computational experiments on a Minimum-Sum-of-Squares problem. Our numerical results demonstrate that the new method provides better solutions while still remains faster than DCA in the majority of test cases.

A Hybrid Stochastic Optimization Framework for Stochastic Composite Nonconvex Optimization

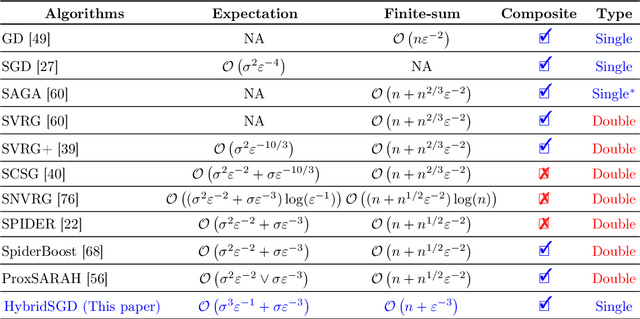
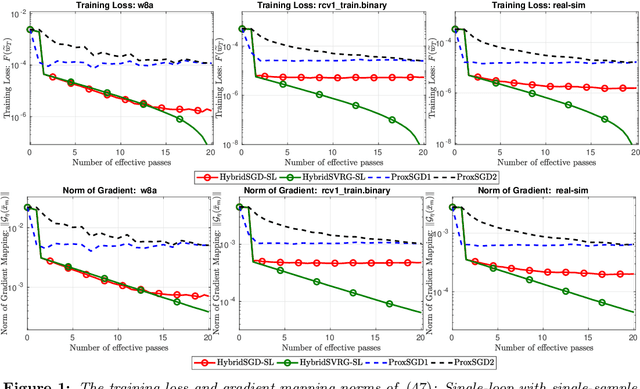
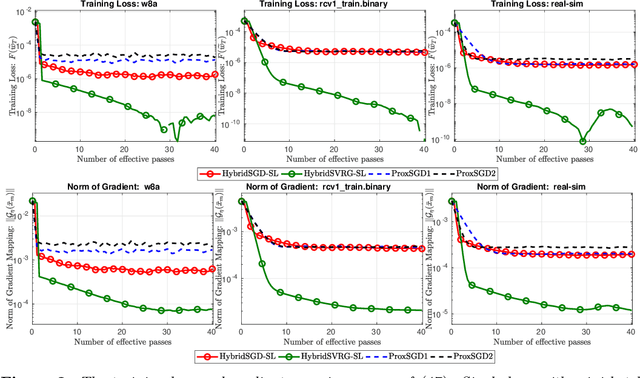
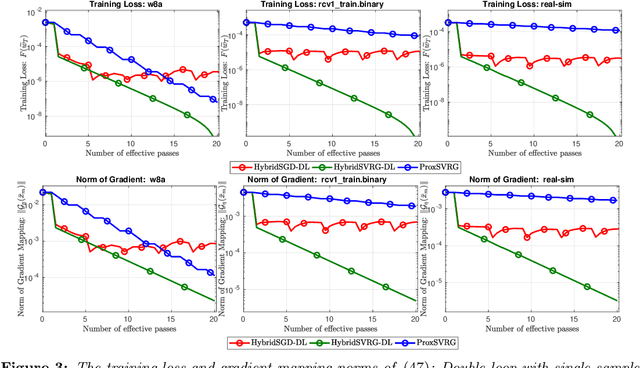
In this paper, we introduce a new approach to develop stochastic optimization algorithms for solving stochastic composite and possibly nonconvex optimization problems. The main idea is to combine two stochastic estimators to form a new hybrid one. We first introduce our hybrid estimator and then investigate its fundamental properties to form a foundation theory for algorithmic development. Next, we apply our theory to develop several variants of stochastic gradient methods to solve both expectation and finite-sum composite optimization problems. Our first algorithm can be viewed as a variant of proximal stochastic gradient methods with a single-loop, but can achieve $\mathcal{O}(\sigma^3\varepsilon^{-1} + \sigma\varepsilon^{-3})$ complexity bound that is significantly better than the $\mathcal{O}(\sigma^2\varepsilon^{-4})$-complexity in state-of-the-art stochastic gradient methods, where $\sigma$ is the variance and $\varepsilon$ is a desired accuracy. Then, we consider two different variants of our method: adaptive step-size and double-loop schemes that have the same theoretical guarantees as in our first algorithm. We also study two mini-batch variants and develop two hybrid SARAH-SVRG algorithms to solve the finite-sum problems. In all cases, we achieve the best-known complexity bounds under standard assumptions. We test our methods on several numerical examples with real datasets and compare them with state-of-the-arts. Our numerical experiments show that the new methods are comparable and, in many cases, outperform their competitors.

Hybrid Stochastic Gradient Descent Algorithms for Stochastic Nonconvex Optimization

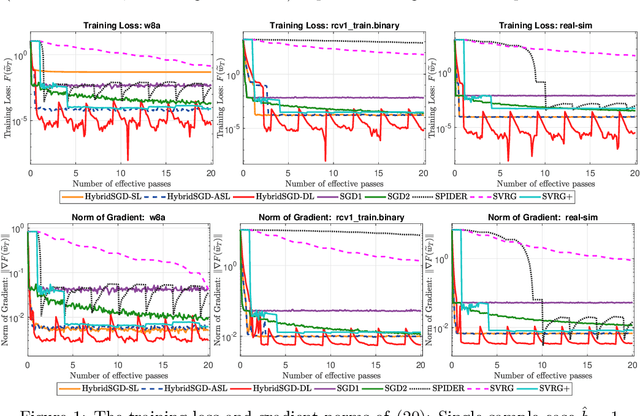
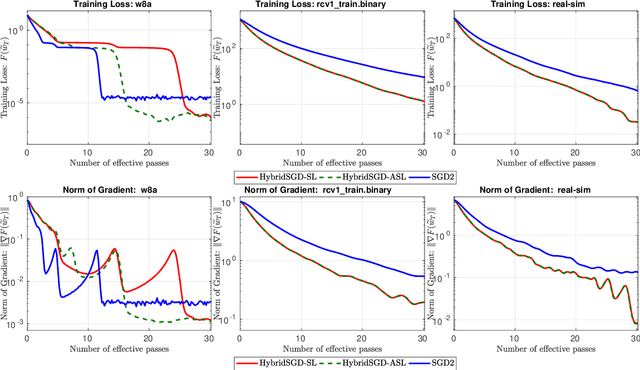
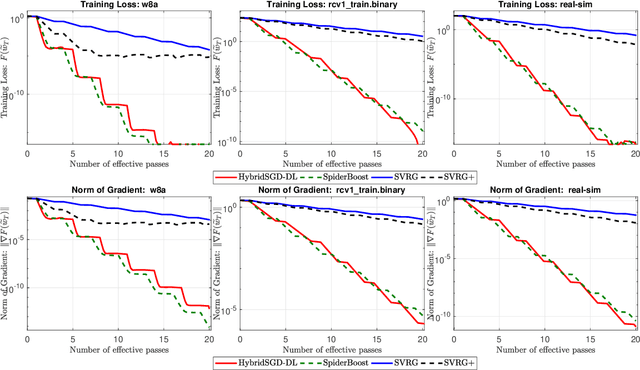
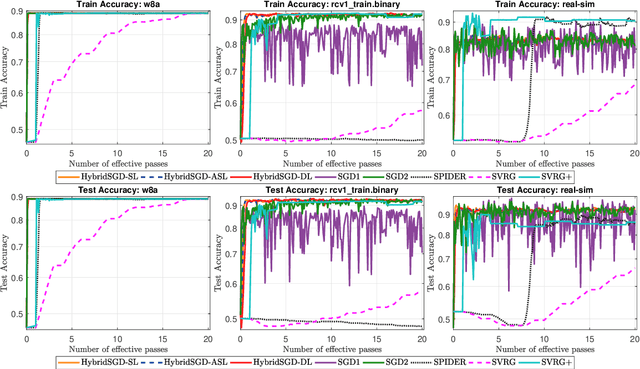
We introduce a hybrid stochastic estimator to design stochastic gradient algorithms for solving stochastic optimization problems. Such a hybrid estimator is a convex combination of two existing biased and unbiased estimators and leads to some useful property on its variance. We limit our consideration to a hybrid SARAH-SGD for nonconvex expectation problems. However, our idea can be extended to handle a broader class of estimators in both convex and nonconvex settings. We propose a new single-loop stochastic gradient descent algorithm that can achieve $O(\max\{\sigma^3\varepsilon^{-1},\sigma\varepsilon^{-3}\})$-complexity bound to obtain an $\varepsilon$-stationary point under smoothness and $\sigma^2$-bounded variance assumptions. This complexity is better than $O(\sigma^2\varepsilon^{-4})$ often obtained in state-of-the-art SGDs when $\sigma < O(\varepsilon^{-3})$. We also consider different extensions of our method, including constant and adaptive step-size with single-loop, double-loop, and mini-batch variants. We compare our algorithms with existing methods on several datasets using two nonconvex models.

ProxSARAH: An Efficient Algorithmic Framework for Stochastic Composite Nonconvex Optimization

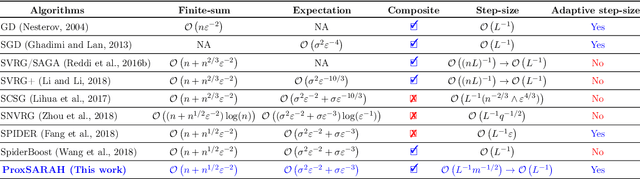
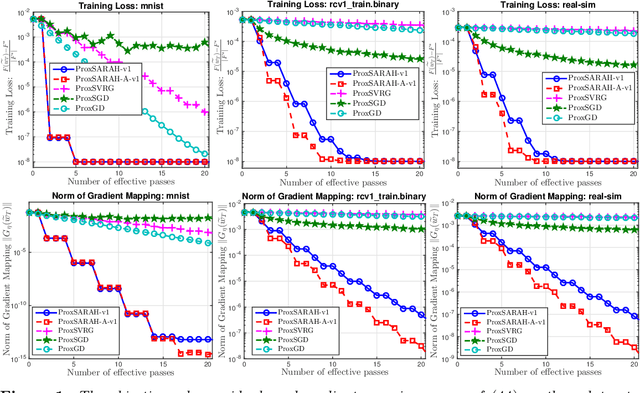
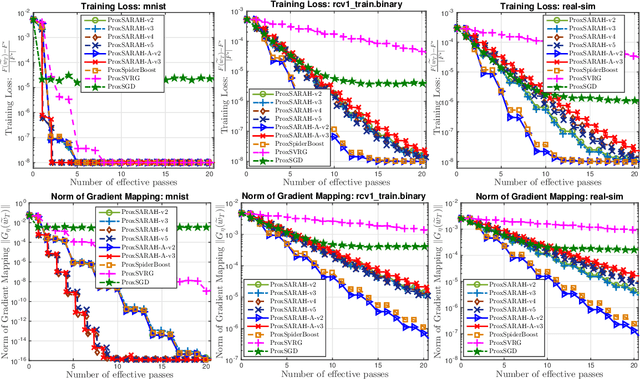
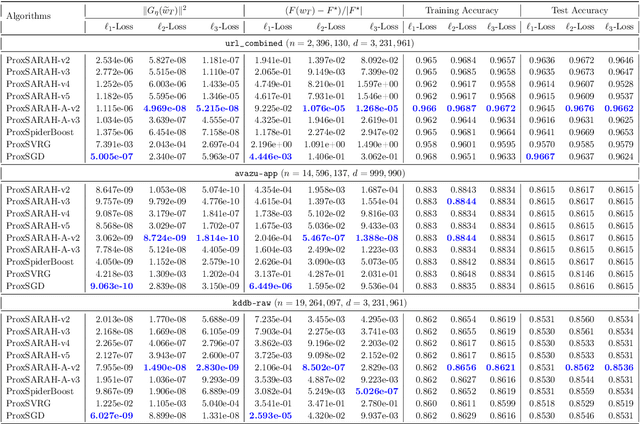
We propose a new stochastic first-order algorithmic framework to solve stochastic composite nonconvex optimization problems that covers both finite-sum and expectation settings. Our algorithms rely on the SARAH estimator introduced in (Nguyen et al, 2017) and consist of two steps: a proximal gradient and an averaging step making them different from existing nonconvex proximal-type algorithms. The algorithms only require an average smoothness assumption of the nonconvex objective term and additional bounded variance assumption if applied to expectation problems. They work with both constant and adaptive step-sizes, while allowing single sample and mini-batches. In all these cases, we prove that our algorithms can achieve the best-known complexity bounds. One key step of our methods is new constant and adaptive step-sizes that help to achieve desired complexity bounds while improving practical performance. Our constant step-size is much larger than existing methods including proximal SVRG schemes in the single sample case. We also specify the algorithm to the non-composite case that covers existing state-of-the-arts in terms of complexity bounds. Our update also allows one to trade-off between step-sizes and mini-batch sizes to improve performance. We test the proposed algorithms on two composite nonconvex problems and neural networks using several well-known datasets.

Non-stationary Douglas-Rachford and alternating direction method of multipliers: adaptive stepsizes and convergence

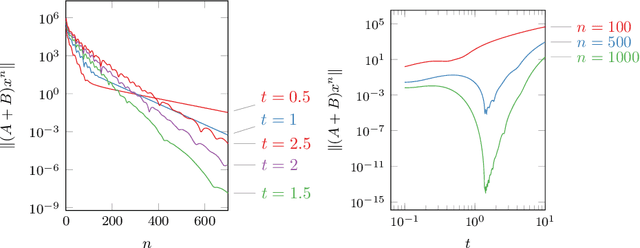
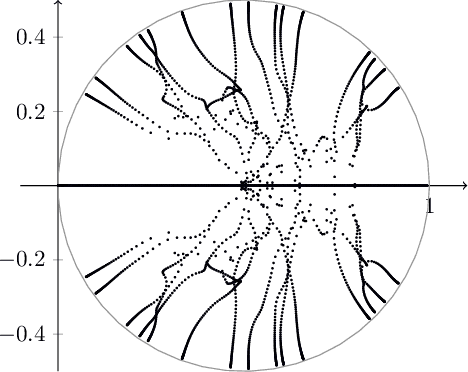
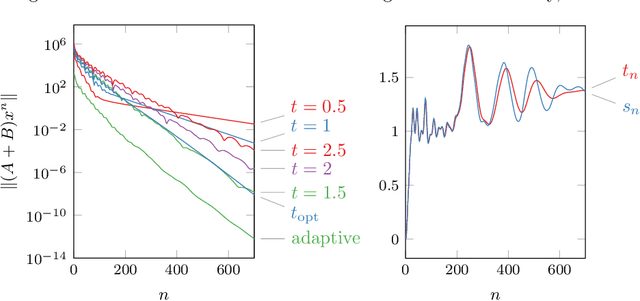
We revisit the classical Douglas-Rachford (DR) method for finding a zero of the sum of two maximal monotone operators. Since the practical performance of the DR method crucially depends on the stepsizes, we aim at developing an adaptive stepsize rule. To that end, we take a closer look at a linear case of the problem and use our findings to develop a stepsize strategy that eliminates the need for stepsize tuning. We analyze a general non-stationary DR scheme and prove its convergence for a convergent sequence of stepsizes with summable increments. This, in turn, proves the convergence of the method with the new adaptive stepsize rule. We also derive the related non-stationary alternating direction method of multipliers (ADMM) from such a non-stationary DR method. We illustrate the efficiency of the proposed methods on several numerical examples.

Generalized Self-Concordant Functions: A Recipe for Newton-Type Methods

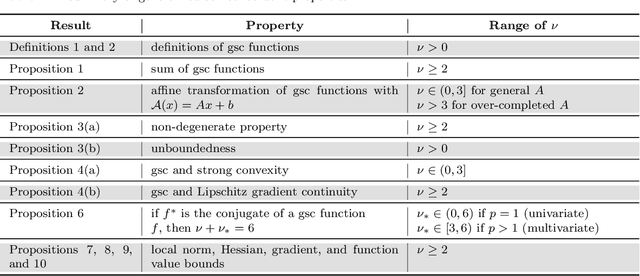
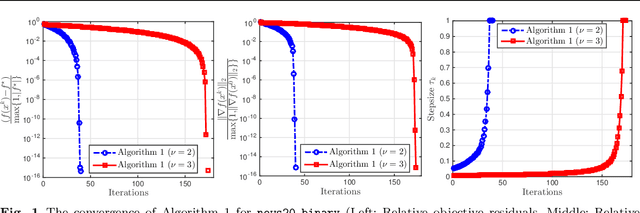
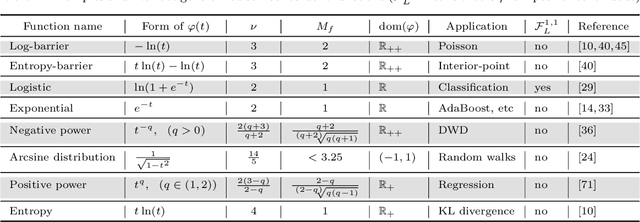
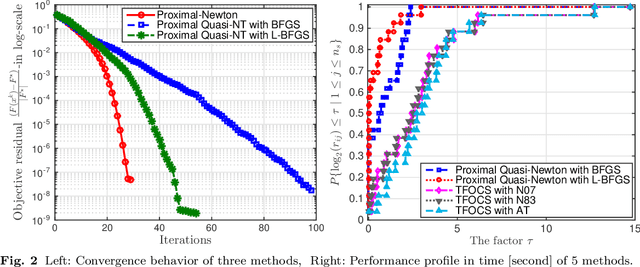
We study the smooth structure of convex functions by generalizing a powerful concept so-called self-concordance introduced by Nesterov and Nemirovskii in the early 1990s to a broader class of convex functions, which we call generalized self-concordant functions. This notion allows us to develop a unified framework for designing Newton-type methods to solve convex optimiza- tion problems. The proposed theory provides a mathematical tool to analyze both local and global convergence of Newton-type methods without imposing unverifiable assumptions as long as the un- derlying functionals fall into our generalized self-concordant function class. First, we introduce the class of generalized self-concordant functions, which covers standard self-concordant functions as a special case. Next, we establish several properties and key estimates of this function class, which can be used to design numerical methods. Then, we apply this theory to develop several Newton-type methods for solving a class of smooth convex optimization problems involving the generalized self- concordant functions. We provide an explicit step-size for the damped-step Newton-type scheme which can guarantee a global convergence without performing any globalization strategy. We also prove a local quadratic convergence of this method and its full-step variant without requiring the Lipschitz continuity of the objective Hessian. Then, we extend our result to develop proximal Newton-type methods for a class of composite convex minimization problems involving generalized self-concordant functions. We also achieve both global and local convergence without additional assumption. Finally, we verify our theoretical results via several numerical examples, and compare them with existing methods.

Composite convex minimization involving self-concordant-like cost functions

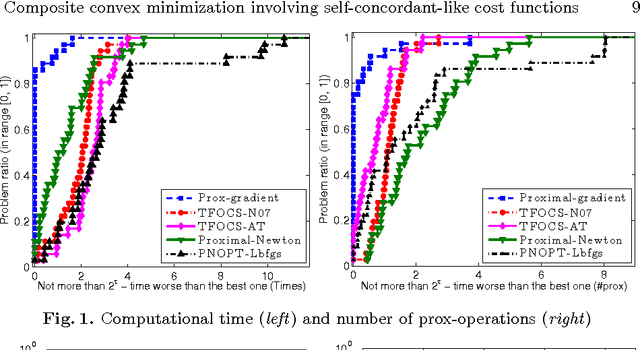
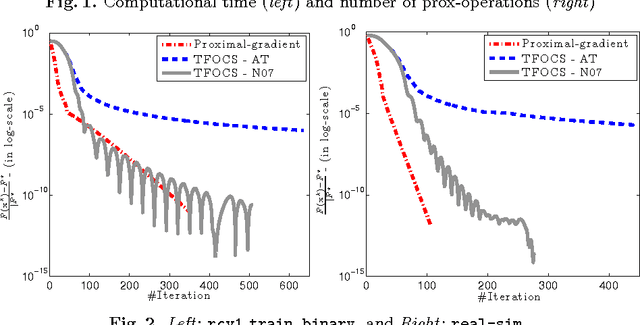
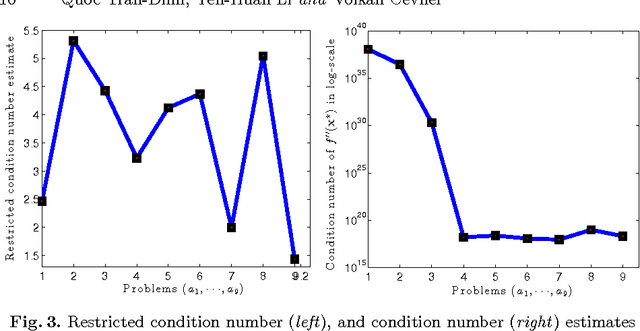
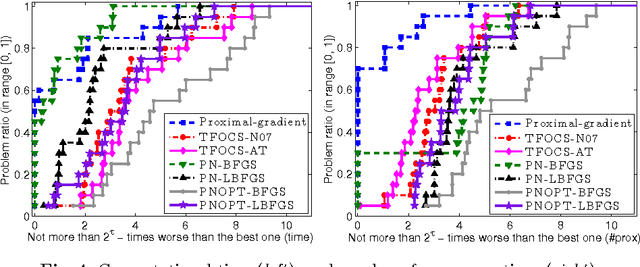
The self-concordant-like property of a smooth convex function is a new analytical structure that generalizes the self-concordant notion. While a wide variety of important applications feature the self-concordant-like property, this concept has heretofore remained unexploited in convex optimization. To this end, we develop a variable metric framework of minimizing the sum of a "simple" convex function and a self-concordant-like function. We introduce a new analytic step-size selection procedure and prove that the basic gradient algorithm has improved convergence guarantees as compared to "fast" algorithms that rely on the Lipschitz gradient property. Our numerical tests with real-data sets shows that the practice indeed follows the theory.