Pranjal Awasthi
Towards Learning Sparsely Used Dictionaries with Arbitrary Supports
May 08, 2018Abstract:Dictionary learning is a popular approach for inferring a hidden basis or dictionary in which data has a sparse representation. Data generated from the dictionary A (an n by m matrix, with m > n in the over-complete setting) is given by Y = AX where X is a matrix whose columns have supports chosen from a distribution over k-sparse vectors, and the non-zero values chosen from a symmetric distribution. Given Y, the goal is to recover A and X in polynomial time. Existing algorithms give polytime guarantees for recovering incoherent dictionaries, under strong distributional assumptions both on the supports of the columns of X, and on the values of the non-zero entries. In this work, we study the following question: Can we design efficient algorithms for recovering dictionaries when the supports of the columns of X are arbitrary? To address this question while circumventing the issue of non-identifiability, we study a natural semirandom model for dictionary learning where there are a large number of samples $y=Ax$ with arbitrary k-sparse supports for x, along with a few samples where the sparse supports are chosen uniformly at random. While the few samples with random supports ensures identifiability, the support distribution can look almost arbitrary in aggregate. Hence existing algorithmic techniques seem to break down as they make strong assumptions on the supports. Our main contribution is a new polynomial time algorithm for learning incoherent over-complete dictionaries that works under the semirandom model. Additionally the same algorithm provides polynomial time guarantees in new parameter regimes when the supports are fully random. Finally using these techniques, we also identify a minimal set of conditions on the supports under which the dictionary can be (information theoretically) recovered from polynomial samples for almost linear sparsity, i.e., $k=\tilde{O}(n)$.
Clustering Semi-Random Mixtures of Gaussians
Nov 23, 2017Abstract:Gaussian mixture models (GMM) are the most widely used statistical model for the $k$-means clustering problem and form a popular framework for clustering in machine learning and data analysis. In this paper, we propose a natural semi-random model for $k$-means clustering that generalizes the Gaussian mixture model, and that we believe will be useful in identifying robust algorithms. In our model, a semi-random adversary is allowed to make arbitrary "monotone" or helpful changes to the data generated from the Gaussian mixture model. Our first contribution is a polynomial time algorithm that provably recovers the ground-truth up to small classification error w.h.p., assuming certain separation between the components. Perhaps surprisingly, the algorithm we analyze is the popular Lloyd's algorithm for $k$-means clustering that is the method-of-choice in practice. Our second result complements the upper bound by giving a nearly matching information-theoretic lower bound on the number of misclassified points incurred by any $k$-means clustering algorithm on the semi-random model.
General and Robust Communication-Efficient Algorithms for Distributed Clustering
Oct 12, 2017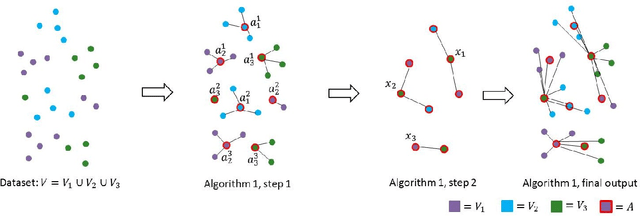
Abstract:As datasets become larger and more distributed, algorithms for distributed clustering have become more and more important. In this work, we present a general framework for designing distributed clustering algorithms that are robust to outliers. Using our framework, we give a distributed approximation algorithm for k-means, k-median, or generally any L_p objective, with z outliers and/or balance constraints, using O(m(k+z)(d+log n)) bits of communication, where m is the number of machines, n is the size of the point set, and d is the dimension. This generalizes and improves over previous work of Bateni et al. and Malkomes et al. As a special case, we achieve the first distributed algorithm for k-median with outliers, answering an open question posed by Malkomes et al. For distributed k-means clustering, we provide the first dimension-dependent communication complexity lower bound for finding the optimal clustering. This improves over the lower bound from Chen et al. which is dimension-agnostic. Furthermore, we give distributed clustering algorithms which return nearly optimal solutions, provided the data satisfies the approximation stability condition of Balcan et al. or the spectral stability condition of Kumar and Kannan.
Efficient PAC Learning from the Crowd
Apr 13, 2017Abstract:In recent years crowdsourcing has become the method of choice for gathering labeled training data for learning algorithms. Standard approaches to crowdsourcing view the process of acquiring labeled data separately from the process of learning a classifier from the gathered data. This can give rise to computational and statistical challenges. For example, in most cases there are no known computationally efficient learning algorithms that are robust to the high level of noise that exists in crowdsourced data, and efforts to eliminate noise through voting often require a large number of queries per example. In this paper, we show how by interleaving the process of labeling and learning, we can attain computational efficiency with much less overhead in the labeling cost. In particular, we consider the realizable setting where there exists a true target function in $\mathcal{F}$ and consider a pool of labelers. When a noticeable fraction of the labelers are perfect, and the rest behave arbitrarily, we show that any $\mathcal{F}$ that can be efficiently learned in the traditional realizable PAC model can be learned in a computationally efficient manner by querying the crowd, despite high amounts of noise in the responses. Moreover, we show that this can be done while each labeler only labels a constant number of examples and the number of labels requested per example, on average, is a constant. When no perfect labelers exist, a related task is to find a set of the labelers which are good but not perfect. We show that we can identify all good labelers, when at least the majority of labelers are good.
Label optimal regret bounds for online local learning
Aug 24, 2015Abstract:We resolve an open question from (Christiano, 2014b) posed in COLT'14 regarding the optimal dependency of the regret achievable for online local learning on the size of the label set. In this framework the algorithm is shown a pair of items at each step, chosen from a set of $n$ items. The learner then predicts a label for each item, from a label set of size $L$ and receives a real valued payoff. This is a natural framework which captures many interesting scenarios such as collaborative filtering, online gambling, and online max cut among others. (Christiano, 2014a) designed an efficient online learning algorithm for this problem achieving a regret of $O(\sqrt{nL^3T})$, where $T$ is the number of rounds. Information theoretically, one can achieve a regret of $O(\sqrt{n \log L T})$. One of the main open questions left in this framework concerns closing the above gap. In this work, we provide a complete answer to the question above via two main results. We show, via a tighter analysis, that the semi-definite programming based algorithm of (Christiano, 2014a), in fact achieves a regret of $O(\sqrt{nLT})$. Second, we show a matching computational lower bound. Namely, we show that a polynomial time algorithm for online local learning with lower regret would imply a polynomial time algorithm for the planted clique problem which is widely believed to be hard. We prove a similar hardness result under a related conjecture concerning planted dense subgraphs that we put forth. Unlike planted clique, the planted dense subgraph problem does not have any known quasi-polynomial time algorithms. Computational lower bounds for online learning are relatively rare, and we hope that the ideas developed in this work will lead to lower bounds for other online learning scenarios as well.
On some provably correct cases of variational inference for topic models
Aug 22, 2015Abstract:Variational inference is a very efficient and popular heuristic used in various forms in the context of latent variable models. It's closely related to Expectation Maximization (EM), and is applied when exact EM is computationally infeasible. Despite being immensely popular, current theoretical understanding of the effectiveness of variaitonal inference based algorithms is very limited. In this work we provide the first analysis of instances where variational inference algorithms converge to the global optimum, in the setting of topic models. More specifically, we show that variational inference provably learns the optimal parameters of a topic model under natural assumptions on the topic-word matrix and the topic priors. The properties that the topic word matrix must satisfy in our setting are related to the topic expansion assumption introduced in (Anandkumar et al., 2013), as well as the anchor words assumption in (Arora et al., 2012c). The assumptions on the topic priors are related to the well known Dirichlet prior, introduced to the area of topic modeling by (Blei et al., 2003). It is well known that initialization plays a crucial role in how well variational based algorithms perform in practice. The initializations that we use are fairly natural. One of them is similar to what is currently used in LDA-c, the most popular implementation of variational inference for topic models. The other one is an overlapping clustering algorithm, inspired by a work by (Arora et al., 2014) on dictionary learning, which is very simple and efficient. While our primary goal is to provide insights into when variational inference might work in practice, the multiplicative, rather than the additive nature of the variational inference updates forces us to use fairly non-standard proof arguments, which we believe will be of general interest.
Relax, no need to round: integrality of clustering formulations
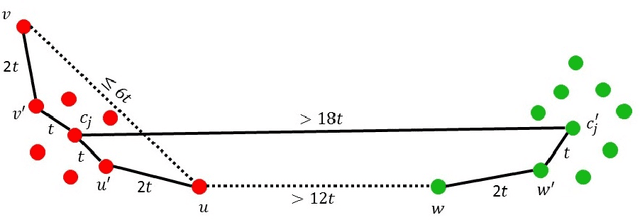
Apr 15, 2015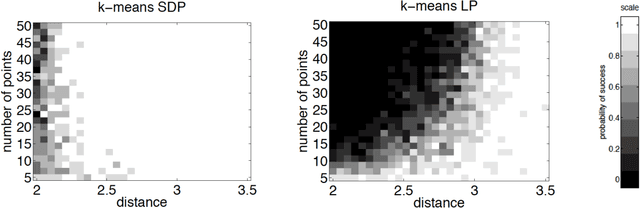
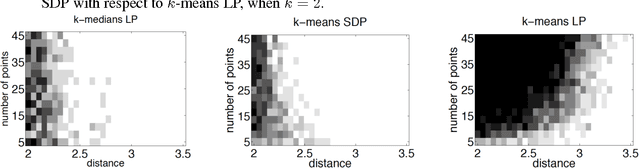
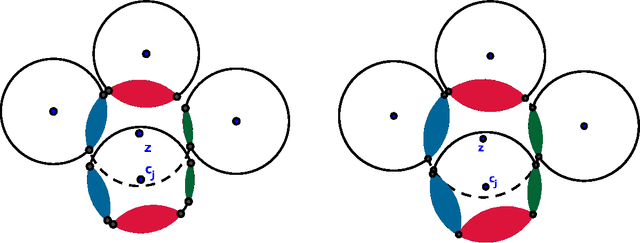
Abstract:We study exact recovery conditions for convex relaxations of point cloud clustering problems, focusing on two of the most common optimization problems for unsupervised clustering: $k$-means and $k$-median clustering. Motivations for focusing on convex relaxations are: (a) they come with a certificate of optimality, and (b) they are generic tools which are relatively parameter-free, not tailored to specific assumptions over the input. More precisely, we consider the distributional setting where there are $k$ clusters in $\mathbb{R}^m$ and data from each cluster consists of $n$ points sampled from a symmetric distribution within a ball of unit radius. We ask: what is the minimal separation distance between cluster centers needed for convex relaxations to exactly recover these $k$ clusters as the optimal integral solution? For the $k$-median linear programming relaxation we show a tight bound: exact recovery is obtained given arbitrarily small pairwise separation $\epsilon > 0$ between the balls. In other words, the pairwise center separation is $\Delta > 2+\epsilon$. Under the same distributional model, the $k$-means LP relaxation fails to recover such clusters at separation as large as $\Delta = 4$. Yet, if we enforce PSD constraints on the $k$-means LP, we get exact cluster recovery at center separation $\Delta > 2\sqrt2(1+\sqrt{1/m})$. In contrast, common heuristics such as Lloyd's algorithm (a.k.a. the $k$-means algorithm) can fail to recover clusters in this setting; even with arbitrarily large cluster separation, k-means++ with overseeding by any constant factor fails with high probability at exact cluster recovery. To complement the theoretical analysis, we provide an experimental study of the recovery guarantees for these various methods, and discuss several open problems which these experiments suggest.
Local algorithms for interactive clustering
Mar 19, 2015

Abstract:We study the design of interactive clustering algorithms for data sets satisfying natural stability assumptions. Our algorithms start with any initial clustering and only make local changes in each step; both are desirable features in many applications. We show that in this constrained setting one can still design provably efficient algorithms that produce accurate clusterings. We also show that our algorithms perform well on real-world data.
Efficient Learning of Linear Separators under Bounded Noise
Mar 12, 2015Abstract:We study the learnability of linear separators in $\Re^d$ in the presence of bounded (a.k.a Massart) noise. This is a realistic generalization of the random classification noise model, where the adversary can flip each example $x$ with probability $\eta(x) \leq \eta$. We provide the first polynomial time algorithm that can learn linear separators to arbitrarily small excess error in this noise model under the uniform distribution over the unit ball in $\Re^d$, for some constant value of $\eta$. While widely studied in the statistical learning theory community in the context of getting faster convergence rates, computationally efficient algorithms in this model had remained elusive. Our work provides the first evidence that one can indeed design algorithms achieving arbitrarily small excess error in polynomial time under this realistic noise model and thus opens up a new and exciting line of research. We additionally provide lower bounds showing that popular algorithms such as hinge loss minimization and averaging cannot lead to arbitrarily small excess error under Massart noise, even under the uniform distribution. Our work instead, makes use of a margin based technique developed in the context of active learning. As a result, our algorithm is also an active learning algorithm with label complexity that is only a logarithmic the desired excess error $\epsilon$.
Learning Mixtures of Ranking Models
Oct 31, 2014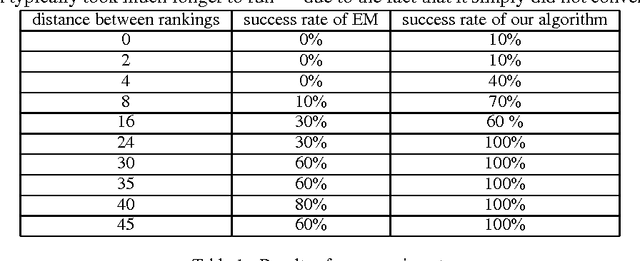
Abstract:This work concerns learning probabilistic models for ranking data in a heterogeneous population. The specific problem we study is learning the parameters of a Mallows Mixture Model. Despite being widely studied, current heuristics for this problem do not have theoretical guarantees and can get stuck in bad local optima. We present the first polynomial time algorithm which provably learns the parameters of a mixture of two Mallows models. A key component of our algorithm is a novel use of tensor decomposition techniques to learn the top-k prefix in both the rankings. Before this work, even the question of identifiability in the case of a mixture of two Mallows models was unresolved.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge