Adversarial Learning Guarantees for Linear Hypotheses and Neural Networks

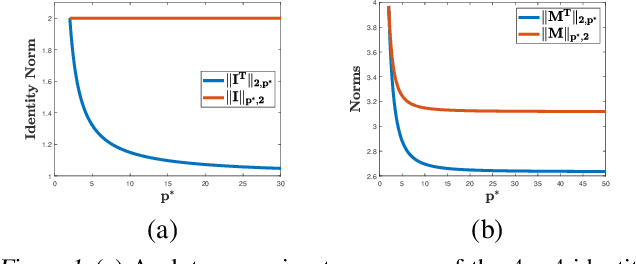
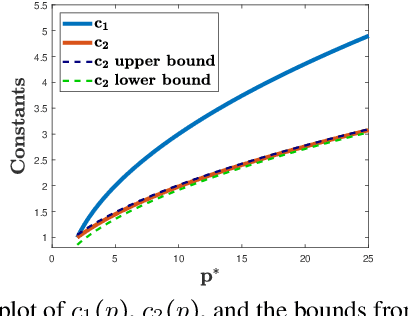
Adversarial or test time robustness measures the susceptibility of a classifier to perturbations to the test input. While there has been a flurry of recent work on designing defenses against such perturbations, the theory of adversarial robustness is not well understood. In order to make progress on this, we focus on the problem of understanding generalization in adversarial settings, via the lens of Rademacher complexity. We give upper and lower bounds for the adversarial empirical Rademacher complexity of linear hypotheses with adversarial perturbations measured in $l_r$-norm for an arbitrary $r \geq 1$. This generalizes the recent result of [Yin et al.'19] that studies the case of $r = \infty$, and provides a finer analysis of the dependence on the input dimensionality as compared to the recent work of [Khim and Loh'19] on linear hypothesis classes. We then extend our analysis to provide Rademacher complexity lower and upper bounds for a single ReLU unit. Finally, we give adversarial Rademacher complexity bounds for feed-forward neural networks with one hidden layer. Unlike previous works we directly provide bounds on the adversarial Rademacher complexity of the given network, as opposed to a bound on a surrogate. A by-product of our analysis also leads to tighter bounds for the Rademacher complexity of linear hypotheses, for which we give a detailed analysis and present a comparison with existing bounds.

Efficient active learning of sparse halfspaces with arbitrary bounded noise

In this work we study active learning of homogeneous $s$-sparse halfspaces in $\mathbb{R}^d$ under label noise. Even in the absence of label noise this is a challenging problem and only recently have label complexity bounds of the form $\tilde{O} \left(s \cdot \mathrm{polylog}(d, \frac{1}{\epsilon}) \right)$ been established in \citet{zhang2018efficient} for computationally efficient algorithms under the broad class of isotropic log-concave distributions. In contrast, under high levels of label noise, the label complexity bounds achieved by computationally efficient algorithms are much worse. When the label noise satisfies the {\em Massart} condition~\citep{massart2006risk}, i.e., each label is flipped with probability at most $\eta$ for a parameter $\eta \in [0,\frac 1 2)$, the work of \citet{awasthi2016learning} provides a computationally efficient active learning algorithm under isotropic log-concave distributions with label complexity $\tilde{O} \left(s^{\mathrm{poly}{(1/(1-2\eta))}} \mathrm{poly}(\log d, \frac{1}{\epsilon}) \right)$. Hence the algorithm is label-efficient only when the noise rate $\eta$ is a constant. In this work, we substantially improve on the state of the art by designing a polynomial time algorithm for active learning of $s$-sparse halfspaces under bounded noise and isotropic log-concave distributions, with a label complexity of $\tilde{O} \left(\frac{s}{(1-2\eta)^4} \mathrm{polylog} (d, \frac 1 \epsilon) \right)$. Hence, our new algorithm is label-efficient even for noise rates close to $\frac{1}{2}$. Prior to our work, such a result was not known even for the random classification noise model. Our algorithm builds upon existing margin-based algorithmic framework and at each iteration performs a sequence of online mirror descent updates on a carefully chosen loss sequence, and uses a novel gradient update rule that accounts for the bounded noise.

A Deep Conditioning Treatment of Neural Networks

We study the role of depth in training randomly initialized overparameterized neural networks. We give the first general result showing that depth improves trainability of neural networks by improving the {\em conditioning} of certain kernel matrices of the input data. This result holds for arbitrary non-linear activation functions, and we provide a characterization of the improvement in conditioning as a function of the degree of non-linearity and the depth of the network. We provide versions of the result that hold for training just the top layer of the neural network, as well as for training all layers, via the neural tangent kernel. As applications of these general results, we provide a generalization of the results of Das et al. (2019) showing that learnability of deep random neural networks with arbitrary non-linear activations (under mild assumptions) degrades exponentially with depth. Additionally, we show how benign overfitting can occur in deep neural networks via the results of Bartlett et al. (2019b).

Adversarially Robust Low Dimensional Representations

Adversarial or test time robustness measures the susceptibility of a machine learning system to small perturbations made to the input at test time. This has attracted much interest on the empirical side, since many existing ML systems perform poorly under imperceptible adversarial perturbations to the test inputs. On the other hand, our theoretical understanding of this phenomenon is limited, and has mostly focused on supervised learning tasks. In this work we study the problem of computing adversarially robust representations of data. We formulate a natural extension of Principal Component Analysis (PCA) where the goal is to find a low dimensional subspace to represent the given data with minimum projection error, and that is in addition robust to small perturbations measured in $\ell_q$ norm (say $q=\infty$). Unlike PCA which is solvable in polynomial time, our formulation is computationally intractable to optimize as it captures the well-studied sparse PCA objective. We show the following algorithmic and statistical results. - Polynomial time algorithms in the worst-case that achieve constant factor approximations to the objective while only violating the robustness constraint by a constant factor. - We prove that our formulation (and algorithms) also enjoy significant statistical benefits in terms of sample complexity over standard PCA on account of a "regularization effect", that is formalized using the well-studied spiked covariance model. - Surprisingly, we show that our algorithmic techniques can also be made robust to corruptions in the training data, in addition to yielding representations that are robust at test time! Here an adversary is allowed to corrupt potentially every data point up to a specified amount in the $\ell_q$ norm. We further apply these techniques for mean estimation and clustering under adversarial corruptions to the training data.

On Robustness to Adversarial Examples and Polynomial Optimization

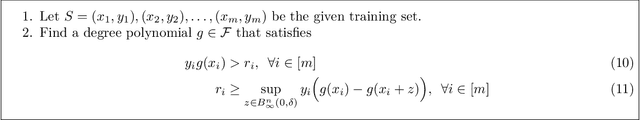
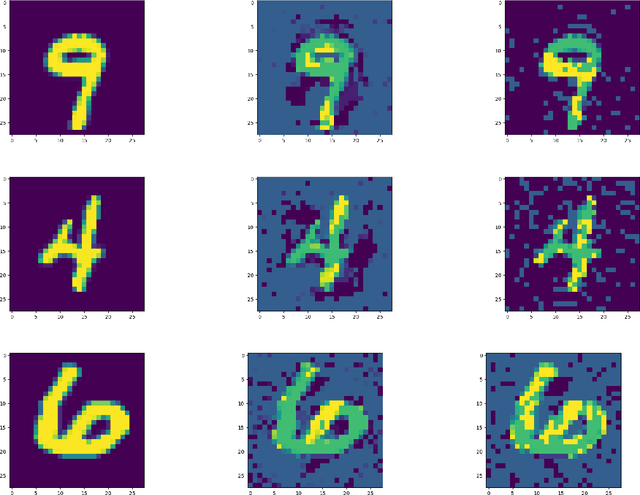
We study the design of computationally efficient algorithms with provable guarantees, that are robust to adversarial (test time) perturbations. While there has been an proliferation of recent work on this topic due to its connections to test time robustness of deep networks, there is limited theoretical understanding of several basic questions like (i) when and how can one design provably robust learning algorithms? (ii) what is the price of achieving robustness to adversarial examples in a computationally efficient manner? The main contribution of this work is to exhibit a strong connection between achieving robustness to adversarial examples, and a rich class of polynomial optimization problems, thereby making progress on the above questions. In particular, we leverage this connection to (a) design computationally efficient robust algorithms with provable guarantees for a large class of hypothesis, namely linear classifiers and degree-2 polynomial threshold functions (PTFs), (b) give a precise characterization of the price of achieving robustness in a computationally efficient manner for these classes, (c) design efficient algorithms to certify robustness and generate adversarial attacks in a principled manner for 2-layer neural networks. We empirically demonstrate the effectiveness of these attacks on real data.

Effectiveness of Equalized Odds for Fair Classification under Imperfect Group Information

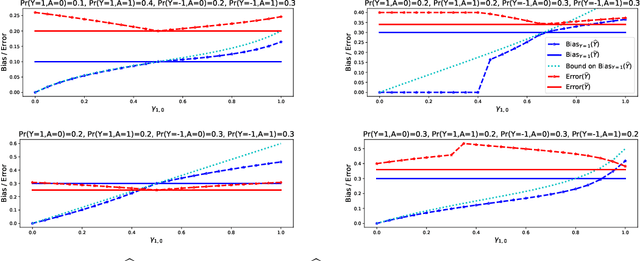
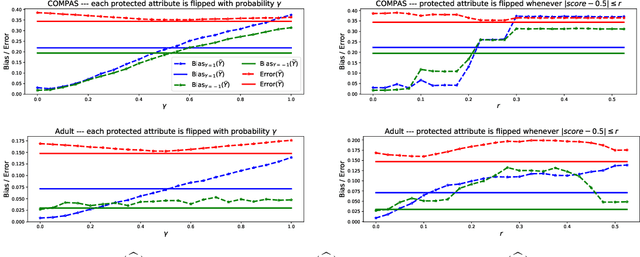
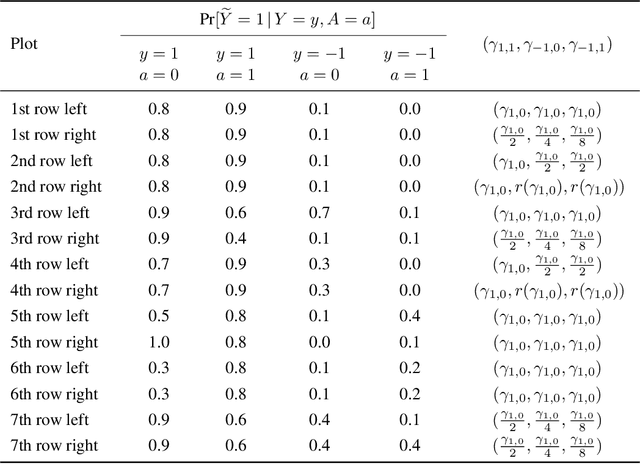
Most approaches for ensuring or improving a model's fairness with respect to a protected attribute (such as race or gender) assume access to the true value of the protected attribute for every data point. In many scenarios, however, perfect knowledge of the protected attribute is unrealistic. In this paper, we ask to what extent fairness interventions can be effective even with imperfect information about the protected attribute. In particular, we study this question in the context of the prominent equalized odds method of Hardt et al. (2016). We claim that as long as the perturbation of the protected attribute is somewhat moderate, one should still run equalized odds if one would run it knowing the true protected attribute: the bias of the classifier that we obtain using the perturbed attribute is smaller than the bias of the original classifier, and its error is not larger than the error of the equalized odds classifier obtained when working with the true protected attribute.

Guarantees for Spectral Clustering with Fairness Constraints

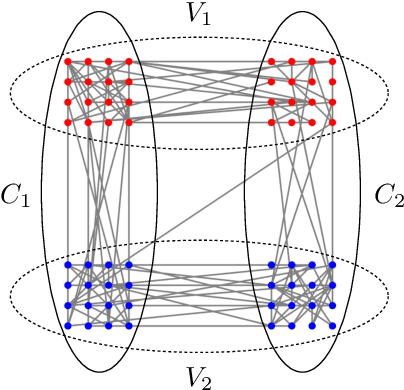
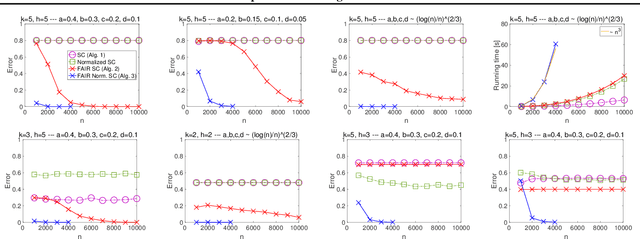
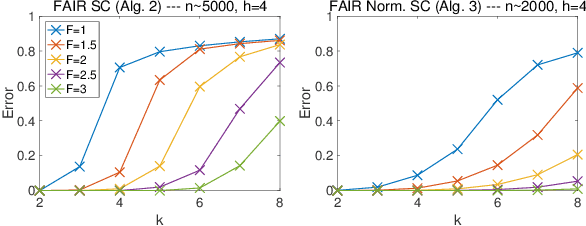
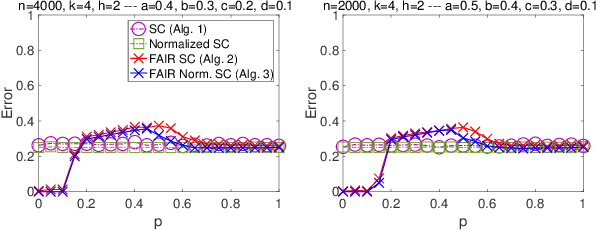
Given the widespread popularity of spectral clustering (SC) for partitioning graph data, we study a version of constrained SC in which we try to incorporate the fairness notion proposed by Chierichetti et al. (2017). According to this notion, a clustering is fair if every demographic group is approximately proportionally represented in each cluster. To this end, we develop variants of both normalized and unnormalized constrained SC and show that they help find fairer clusterings on both synthetic and real data. We also provide a rigorous theoretical analysis of our algorithms. While there have been efforts to incorporate various constraints into the SC framework, theoretically analyzing them is a challenging problem. We overcome this by proposing a natural variant of the stochastic block model where h groups have strong inter-group connectivity, but also exhibit a "natural" clustering structure which is fair. We prove that our algorithms can recover this fair clustering with high probability.

Fair k-Center Clustering for Data Summarization

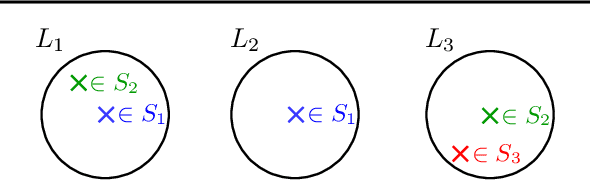
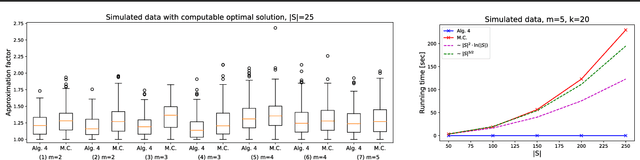
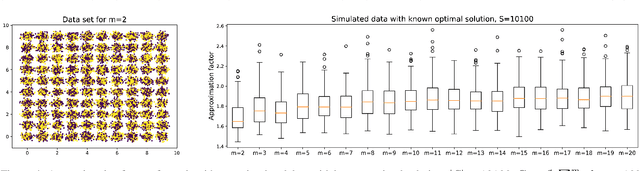
In data summarization we want to choose k prototypes in order to summarize a data set. We study a setting where the data set comprises several demographic groups and we are restricted to choose k_i prototypes belonging to group i. A common approach to the problem without the fairness constraint is to optimize a centroid-based clustering objective such as k-center. A natural extension then is to incorporate the fairness constraint into the clustering objective. Existing algorithms for doing so run in time super-quadratic in the size of the data set. This is in contrast to the standard k-center objective that can be approximately optimized in linear time. In this paper, we resolve this gap by providing a simple approximation algorithm for the k-center problem under the fairness constraint with running time linear in the size of the data set and k. If the number of demographic groups is small, the approximation guarantee of our algorithm only incurs a constant-factor overhead. We demonstrate the applicability of our algorithm on both synthetic and real data sets.

The Power of Localization for Efficiently Learning Linear Separators with Noise

We introduce a new approach for designing computationally efficient learning algorithms that are tolerant to noise, and demonstrate its effectiveness by designing algorithms with improved noise tolerance guarantees for learning linear separators. We consider both the malicious noise model and the adversarial label noise model. For malicious noise, where the adversary can corrupt both the label and the features, we provide a polynomial-time algorithm for learning linear separators in $\Re^d$ under isotropic log-concave distributions that can tolerate a nearly information-theoretically optimal noise rate of $\eta = \Omega(\epsilon)$. For the adversarial label noise model, where the distribution over the feature vectors is unchanged, and the overall probability of a noisy label is constrained to be at most $\eta$, we also give a polynomial-time algorithm for learning linear separators in $\Re^d$ under isotropic log-concave distributions that can handle a noise rate of $\eta = \Omega\left(\epsilon\right)$. We show that, in the active learning model, our algorithms achieve a label complexity whose dependence on the error parameter $\epsilon$ is polylogarithmic. This provides the first polynomial-time active learning algorithm for learning linear separators in the presence of malicious noise or adversarial label noise.

Towards Learning Sparsely Used Dictionaries with Arbitrary Supports

Dictionary learning is a popular approach for inferring a hidden basis or dictionary in which data has a sparse representation. Data generated from the dictionary A (an n by m matrix, with m > n in the over-complete setting) is given by Y = AX where X is a matrix whose columns have supports chosen from a distribution over k-sparse vectors, and the non-zero values chosen from a symmetric distribution. Given Y, the goal is to recover A and X in polynomial time. Existing algorithms give polytime guarantees for recovering incoherent dictionaries, under strong distributional assumptions both on the supports of the columns of X, and on the values of the non-zero entries. In this work, we study the following question: Can we design efficient algorithms for recovering dictionaries when the supports of the columns of X are arbitrary? To address this question while circumventing the issue of non-identifiability, we study a natural semirandom model for dictionary learning where there are a large number of samples $y=Ax$ with arbitrary k-sparse supports for x, along with a few samples where the sparse supports are chosen uniformly at random. While the few samples with random supports ensures identifiability, the support distribution can look almost arbitrary in aggregate. Hence existing algorithmic techniques seem to break down as they make strong assumptions on the supports. Our main contribution is a new polynomial time algorithm for learning incoherent over-complete dictionaries that works under the semirandom model. Additionally the same algorithm provides polynomial time guarantees in new parameter regimes when the supports are fully random. Finally using these techniques, we also identify a minimal set of conditions on the supports under which the dictionary can be (information theoretically) recovered from polynomial samples for almost linear sparsity, i.e., $k=\tilde{O}(n)$.