A Lesion-aware Edge-based Graph Neural Network for Predicting Language Ability in Patients with Post-stroke Aphasia

We propose a lesion-aware graph neural network (LEGNet) to predict language ability from resting-state fMRI (rs-fMRI) connectivity in patients with post-stroke aphasia. Our model integrates three components: an edge-based learning module that encodes functional connectivity between brain regions, a lesion encoding module, and a subgraph learning module that leverages functional similarities for prediction. We use synthetic data derived from the Human Connectome Project (HCP) for hyperparameter tuning and model pretraining. We then evaluate the performance using repeated 10-fold cross-validation on an in-house neuroimaging dataset of post-stroke aphasia. Our results demonstrate that LEGNet outperforms baseline deep learning methods in predicting language ability. LEGNet also exhibits superior generalization ability when tested on a second in-house dataset that was acquired under a slightly different neuroimaging protocol. Taken together, the results of this study highlight the potential of LEGNet in effectively learning the relationships between rs-fMRI connectivity and language ability in a patient cohort with brain lesions for improved post-stroke aphasia evaluation.

Detecting Frames in News Headlines and Lead Images in U.S. Gun Violence Coverage

News media structure their reporting of events or issues using certain perspectives. When describing an incident involving gun violence, for example, some journalists may focus on mental health or gun regulation, while others may emphasize the discussion of gun rights. Such perspectives are called \say{frames} in communication research. We study, for the first time, the value of combining lead images and their contextual information with text to identify the frame of a given news article. We observe that using multiple modes of information(article- and image-derived features) improves prediction of news frames over any single mode of information when the images are relevant to the frames of the headlines. We also observe that frame image relevance is related to the ease of conveying frames via images, which we call frame concreteness. Additionally, we release the first multimodal news framing dataset related to gun violence in the U.S., curated and annotated by communication researchers. The dataset will allow researchers to further examine the use of multiple information modalities for studying media framing.

On neural and dimensional collapse in supervised and unsupervised contrastive learning with hard negative sampling

For a widely-studied data model and general loss and sample-hardening functions we prove that the Supervised Contrastive Learning (SCL), Hard-SCL (HSCL), and Unsupervised Contrastive Learning (UCL) risks are minimized by representations that exhibit Neural Collapse (NC), i.e., the class means form an Equianglular Tight Frame (ETF) and data from the same class are mapped to the same representation. We also prove that for any representation mapping, the HSCL and Hard-UCL (HUCL) risks are lower bounded by the corresponding SCL and UCL risks. Although the optimality of ETF is known for SCL, albeit only for InfoNCE loss, its optimality for HSCL and UCL under general loss and hardening functions is novel. Moreover, our proofs are much simpler, compact, and transparent. We empirically demonstrate, for the first time, that ADAM optimization of HSCL and HUCL risks with random initialization and suitable hardness levels can indeed converge to the NC geometry if we incorporate unit-ball or unit-sphere feature normalization. Without incorporating hard negatives or feature normalization, however, the representations learned via ADAM suffer from dimensional collapse (DC) and fail to attain the NC geometry.

A principled approach to model validation in domain generalization

Domain generalization aims to learn a model with good generalization ability, that is, the learned model should not only perform well on several seen domains but also on unseen domains with different data distributions. State-of-the-art domain generalization methods typically train a representation function followed by a classifier jointly to minimize both the classification risk and the domain discrepancy. However, when it comes to model selection, most of these methods rely on traditional validation routines that select models solely based on the lowest classification risk on the validation set. In this paper, we theoretically demonstrate a trade-off between minimizing classification risk and mitigating domain discrepancy, i.e., it is impossible to achieve the minimum of these two objectives simultaneously. Motivated by this theoretical result, we propose a novel model selection method suggesting that the validation process should account for both the classification risk and the domain discrepancy. We validate the effectiveness of the proposed method by numerical results on several domain generalization datasets.

Estimating Distances Between People using a Single Overhead Fisheye Camera with Application to Social-Distancing Oversight

Unobtrusive monitoring of distances between people indoors is a useful tool in the fight against pandemics. A natural resource to accomplish this are surveillance cameras. Unlike previous distance estimation methods, we use a single, overhead, fisheye camera with wide area coverage and propose two approaches. One method leverages a geometric model of the fisheye lens, whereas the other method uses a neural network to predict the 3D-world distance from people-locations in a fisheye image. To evaluate our algorithms, we collected a first-of-its-kind dataset using single fisheye camera, that comprises a wide range of distances between people (1-58 ft) and will be made publicly available. The algorithms achieve 1-2 ft distance error and over 95% accuracy in detecting social-distance violations.

Spatio-Visual Fusion-Based Person Re-Identification for Overhead Fisheye Images

Reliable and cost-effective counting of people in large indoor spaces is a significant challenge with many applications. An emerging approach is to deploy multiple fisheye cameras mounted overhead to monitor the whole space. However, due to the overlapping fields of view, person re-identificaiton (PRID) is critical for the accuracy of counting. While PRID has been thoroughly researched for traditional rectilinear cameras, few methods have been proposed for fisheye cameras and their performance is comparatively lower. To close this performance gap, we propose a multi-feature framework for fisheye PRID where we combine deep-learning, color-based and location-based features by means of novel feature fusion. We evaluate the performance of our framework for various feature combinations on FRIDA, a public fisheye PRID dataset. The results demonstrate that our multi-feature approach outperforms recent appearance-based deep-learning methods by almost 18% points and location-based methods by almost 3% points in accuracy.

Trade-off between reconstruction loss and feature alignment for domain generalization

Domain generalization (DG) is a branch of transfer learning that aims to train the learning models on several seen domains and subsequently apply these pre-trained models to other unseen (unknown but related) domains. To deal with challenging settings in DG where both data and label of the unseen domain are not available at training time, the most common approach is to design the classifiers based on the domain-invariant representation features, i.e., the latent representations that are unchanged and transferable between domains. Contrary to popular belief, we show that designing classifiers based on invariant representation features alone is necessary but insufficient in DG. Our analysis indicates the necessity of imposing a constraint on the reconstruction loss induced by representation functions to preserve most of the relevant information about the label in the latent space. More importantly, we point out the trade-off between minimizing the reconstruction loss and achieving domain alignment in DG. Our theoretical results motivate a new DG framework that jointly optimizes the reconstruction loss and the domain discrepancy. Both theoretical and numerical results are provided to justify our approach.

FRIDA: Fisheye Re-Identification Dataset with Annotations

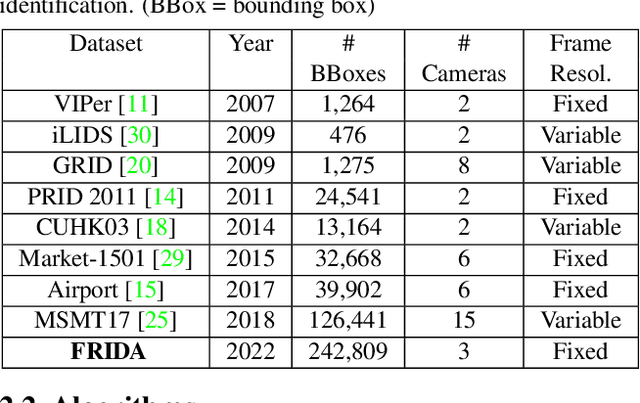
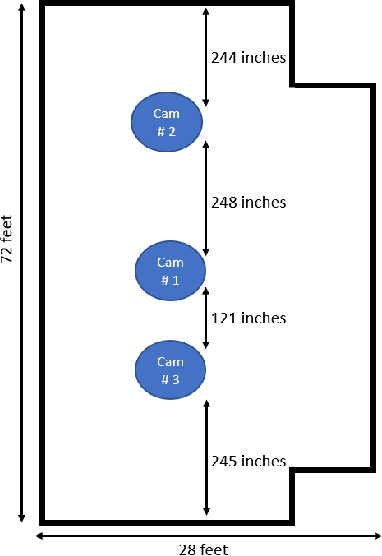
Person re-identification (PRID) from side-mounted rectilinear-lens cameras is a well-studied problem. On the other hand, PRID from overhead fisheye cameras is new and largely unstudied, primarily due to the lack of suitable image datasets. To fill this void, we introduce the "Fisheye Re-IDentification Dataset with Annotations" (FRIDA), with 240k+ bounding-box annotations of people, captured by 3 time-synchronized, ceiling-mounted fisheye cameras in a large indoor space. Due to a field-of-view overlap, PRID in this case differs from a typical PRID problem, which we discuss in depth. We also evaluate the performance of 10 state-of-the-art PRID algorithms on FRIDA. We show that for 6 CNN-based algorithms, training on FRIDA boosts the performance by up to 11.64% points in mAP compared to training on a common rectilinear-camera PRID dataset.

Joint covariate-alignment and concept-alignment: a framework for domain generalization

In this paper, we propose a novel domain generalization (DG) framework based on a new upper bound to the risk on the unseen domain. Particularly, our framework proposes to jointly minimize both the covariate-shift as well as the concept-shift between the seen domains for a better performance on the unseen domain. While the proposed approach can be implemented via an arbitrary combination of covariate-alignment and concept-alignment modules, in this work we use well-established approaches for distributional alignment namely, Maximum Mean Discrepancy (MMD) and covariance Alignment (CORAL), and use an Invariant Risk Minimization (IRM)-based approach for concept alignment. Our numerical results show that the proposed methods perform as well as or better than the state-of-the-art for domain generalization on several data sets.

Conditional entropy minimization principle for learning domain invariant representation features

Invariance principle-based methods, for example, Invariant Risk Minimization (IRM), have recently emerged as promising approaches for Domain Generalization (DG). Despite the promising theory, invariance principle-based approaches fail in common classification tasks due to the mixture of the true invariant features and the spurious invariant features. In this paper, we propose a framework based on the conditional entropy minimization principle to filter out the spurious invariant features leading to a new algorithm with a better generalization capability. We theoretically prove that under some particular assumptions, the representation function can precisely recover the true invariant features. In addition, we also show that the proposed approach is closely related to the well-known Information Bottleneck framework. Both the theoretical and numerical results are provided to justify our approach.