Information-Theoretic Approach to Efficient Adaptive Path Planning for Mobile Robotic Environmental Sensing

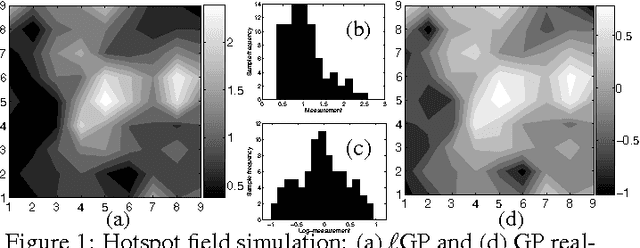
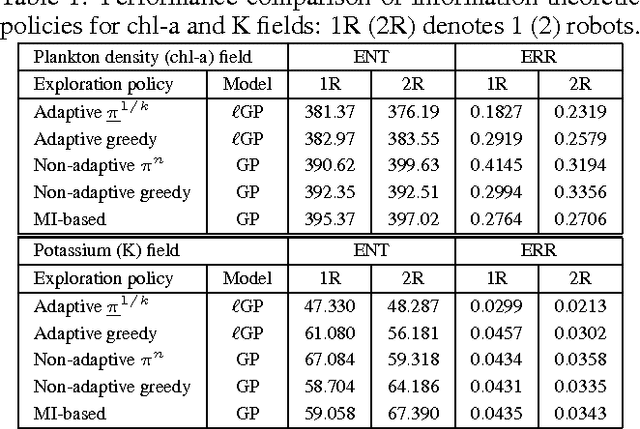
Recent research in robot exploration and mapping has focused on sampling environmental hotspot fields. This exploration task is formalized by Low, Dolan, and Khosla (2008) in a sequential decision-theoretic planning under uncertainty framework called MASP. The time complexity of solving MASP approximately depends on the map resolution, which limits its use in large-scale, high-resolution exploration and mapping. To alleviate this computational difficulty, this paper presents an information-theoretic approach to MASP (iMASP) for efficient adaptive path planning; by reformulating the cost-minimizing iMASP as a reward-maximizing problem, its time complexity becomes independent of map resolution and is less sensitive to increasing robot team size as demonstrated both theoretically and empirically. Using the reward-maximizing dual, we derive a novel adaptive variant of maximum entropy sampling, thus improving the induced exploration policy performance. It also allows us to establish theoretical bounds quantifying the performance advantage of optimal adaptive over non-adaptive policies and the performance quality of approximately optimal vs. optimal adaptive policies. We show analytically and empirically the superior performance of iMASP-based policies for sampling the log-Gaussian process to that of policies for the widely-used Gaussian process in mapping the hotspot field. Lastly, we provide sufficient conditions that, when met, guarantee adaptivity has no benefit under an assumed environment model.

Active Markov Information-Theoretic Path Planning for Robotic Environmental Sensing

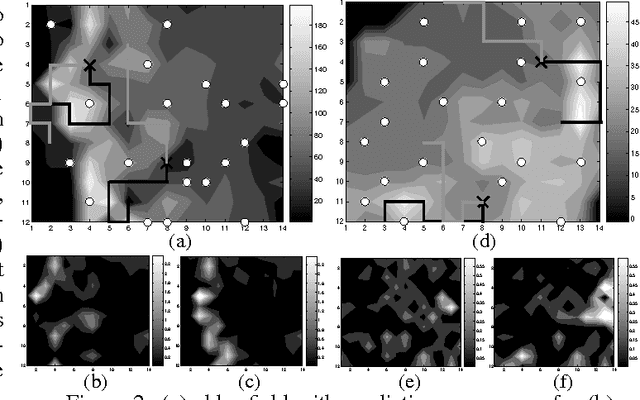
Recent research in multi-robot exploration and mapping has focused on sampling environmental fields, which are typically modeled using the Gaussian process (GP). Existing information-theoretic exploration strategies for learning GP-based environmental field maps adopt the non-Markovian problem structure and consequently scale poorly with the length of history of observations. Hence, it becomes computationally impractical to use these strategies for in situ, real-time active sampling. To ease this computational burden, this paper presents a Markov-based approach to efficient information-theoretic path planning for active sampling of GP-based fields. We analyze the time complexity of solving the Markov-based path planning problem, and demonstrate analytically that it scales better than that of deriving the non-Markovian strategies with increasing length of planning horizon. For a class of exploration tasks called the transect sampling task, we provide theoretical guarantees on the active sampling performance of our Markov-based policy, from which ideal environmental field conditions and sampling task settings can be established to limit its performance degradation due to violation of the Markov assumption. Empirical evaluation on real-world temperature and plankton density field data shows that our Markov-based policy can generally achieve active sampling performance comparable to that of the widely-used non-Markovian greedy policies under less favorable realistic field conditions and task settings while enjoying significant computational gain over them.