Viability of Future Actions: Robust Safety in Reinforcement Learning via Entropy Regularization

Despite the many recent advances in reinforcement learning (RL), the question of learning policies that robustly satisfy state constraints under unknown disturbances remains open. In this paper, we offer a new perspective on achieving robust safety by analyzing the interplay between two well-established techniques in model-free RL: entropy regularization, and constraints penalization. We reveal empirically that entropy regularization in constrained RL inherently biases learning toward maximizing the number of future viable actions, thereby promoting constraints satisfaction robust to action noise. Furthermore, we show that by relaxing strict safety constraints through penalties, the constrained RL problem can be approximated arbitrarily closely by an unconstrained one and thus solved using standard model-free RL. This reformulation preserves both safety and optimality while empirically improving resilience to disturbances. Our results indicate that the connection between entropy regularization and robustness is a promising avenue for further empirical and theoretical investigation, as it enables robust safety in RL through simple reward shaping.

A kernel conditional two-sample test

We propose a framework for hypothesis testing on conditional probability distributions, which we then use to construct conditional two-sample statistical tests. These tests identify the inputs -- called covariates in this context -- where two conditional expectations differ with high probability. Our key idea is to transform confidence bounds of a learning method into a conditional two-sample test, and we instantiate this principle for kernel ridge regression (KRR) and conditional kernel mean embeddings. We generalize existing pointwise-in-time or time-uniform confidence bounds for KRR to previously-inaccessible yet essential cases such as infinite-dimensional outputs with non-trace-class kernels. These bounds enable circumventing the need for independent data in our statistical tests, since they allow online sampling. We also introduce bootstrapping schemes leveraging the parametric form of testing thresholds identified in theory to avoid tuning inaccessible parameters, making our method readily applicable in practice. Such conditional two-sample tests are especially relevant in applications where data arrive sequentially or non-independently, or when output distributions vary with operational parameters. We demonstrate their utility through examples in process monitoring and comparison of dynamical systems. Overall, our results establish a comprehensive foundation for conditional two-sample testing, from theoretical guarantees to practical implementation, and advance the state-of-the-art on the concentration of vector-valued least squares estimation.

On the Consistency of Kernel Methods with Dependent Observations

The consistency of a learning method is usually established under the assumption that the observations are a realization of an independent and identically distributed (i.i.d.) or mixing process. Yet, kernel methods such as support vector machines (SVMs), Gaussian processes, or conditional kernel mean embeddings (CKMEs) all give excellent performance under sampling schemes that are obviously non-i.i.d., such as when data comes from a dynamical system. We propose the new notion of empirical weak convergence (EWC) as a general assumption explaining such phenomena for kernel methods. It assumes the existence of a random asymptotic data distribution and is a strict weakening of previous assumptions in the field. Our main results then establish consistency of SVMs, kernel mean embeddings, and general Hilbert-space valued empirical expectations with EWC data. Our analysis holds for both finite- and infinite-dimensional outputs, as we extend classical results of statistical learning to the latter case. In particular, it is also applicable to CKMEs. Overall, our results open new classes of processes to statistical learning and can serve as a foundation for a theory of learning beyond i.i.d. and mixing.

Data-Driven Observability Analysis for Nonlinear Stochastic Systems

Distinguishability and, by extension, observability are key properties of dynamical systems. Establishing these properties is challenging, especially when no analytical model is available and they are to be inferred directly from measurement data. The presence of noise further complicates this analysis, as standard notions of distinguishability are tailored to deterministic systems. We build on distributional distinguishability, which extends the deterministic notion by comparing distributions of outputs of stochastic systems. We first show that both concepts are equivalent for a class of systems that includes linear systems. We then present a method to assess and quantify distributional distinguishability from output data. Specifically, our quantification measures how much data is required to tell apart two initial states, inducing a continuous spectrum of distinguishability. We propose a statistical test to determine a threshold above which two states can be considered distinguishable with high confidence. We illustrate these tools by computing distinguishability maps over the state space in simulation, then leverage the test to compare sensor configurations on hardware.

Safe Value Functions

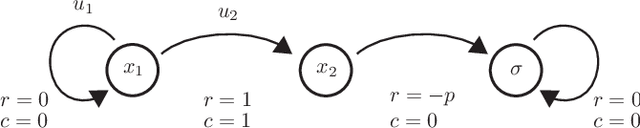
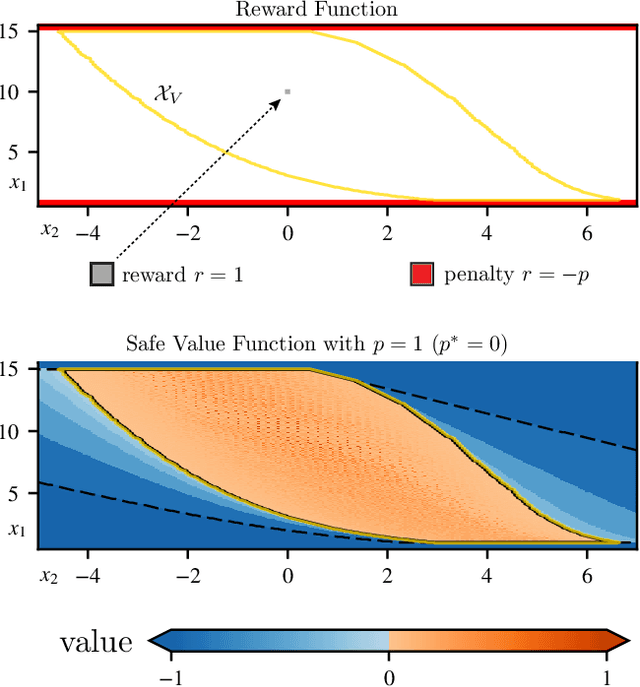
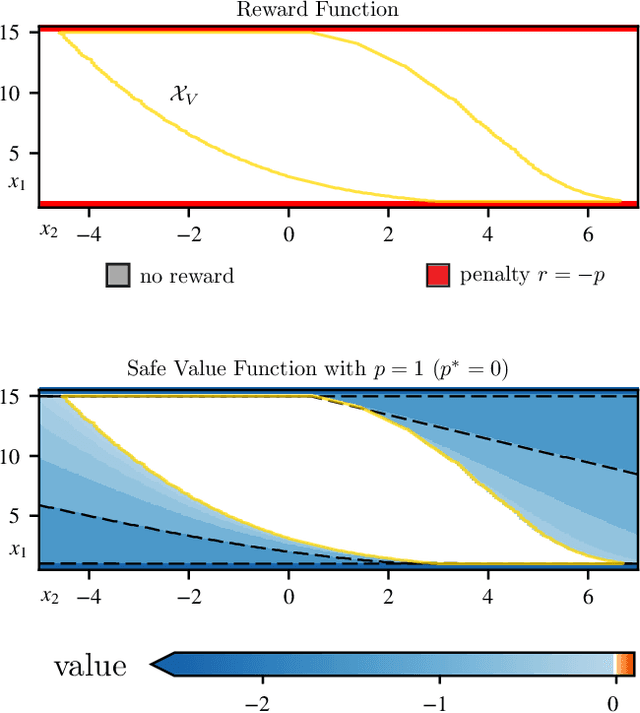
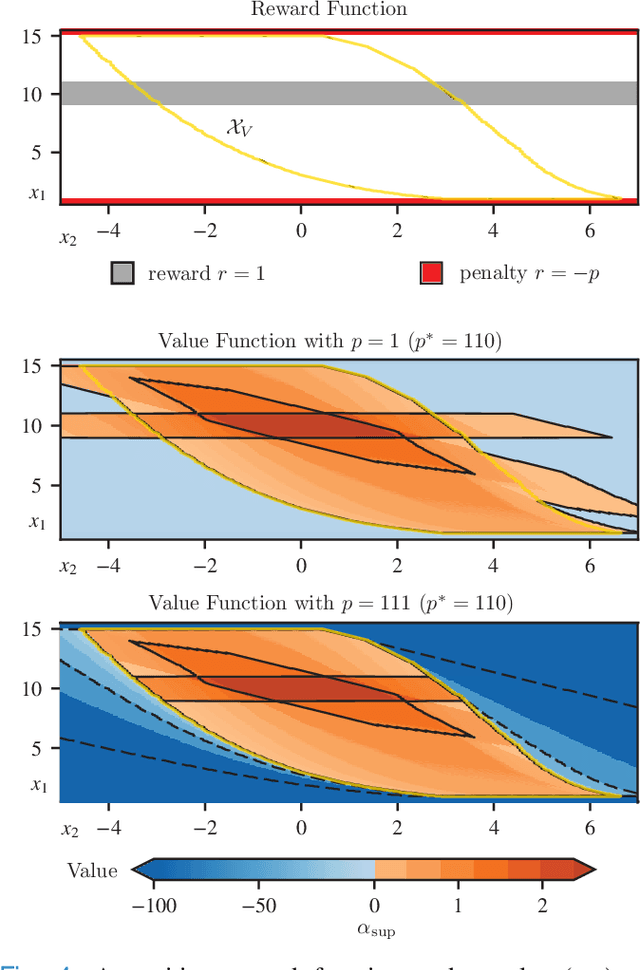
The relationship between safety and optimality in control is not well understood, and they are often seen as important yet conflicting objectives. There is a pressing need to formalize this relationship, especially given the growing prominence of learning-based methods. Indeed, it is common practice in reinforcement learning to simply modify reward functions by penalizing failures, with the penalty treated as a mere heuristic. We rigorously examine this relationship, and formalize the requirements for safe value functions: value functions that are both optimal for a given task, and enforce safety. We reveal the structure of this relationship through a proof of strong duality, showing that there always exists a finite penalty that induces a safe value function. This penalty is not unique, but upper-unbounded: larger penalties do not harm optimality. Although it is often not possible to compute the minimum required penalty, we reveal clear structure of how the penalty, rewards, discount factor, and dynamics interact. This insight suggests practical, theory-guided heuristics to design reward functions for control problems where safety is important.