Domain Generalization for Time Series: Enhancing Drilling Regression Models for Stick-Slip Index Prediction

This paper provides a comprehensive comparison of domain generalization techniques applied to time series data within a drilling context, focusing on the prediction of a continuous Stick-Slip Index (SSI), a critical metric for assessing torsional downhole vibrations at the drill bit. The study aims to develop a robust regression model that can generalize across domains by training on 60 second labeled sequences of 1 Hz surface drilling data to predict the SSI. The model is tested in wells that are different from those used during training. To fine-tune the model architecture, a grid search approach is employed to optimize key hyperparameters. A comparative analysis of the Adversarial Domain Generalization (ADG), Invariant Risk Minimization (IRM) and baseline models is presented, along with an evaluation of the effectiveness of transfer learning (TL) in improving model performance. The ADG and IRM models achieve performance improvements of 10% and 8%, respectively, over the baseline model. Most importantly, severe events are detected 60% of the time, against 20% for the baseline model. Overall, the results indicate that both ADG and IRM models surpass the baseline, with the ADG model exhibiting a slight advantage over the IRM model. Additionally, applying TL to a pre-trained model further improves performance. Our findings demonstrate the potential of domain generalization approaches in drilling applications, with ADG emerging as the most effective approach.

Enabling safe walking rehabilitation on the exoskeleton Atalante: experimental results

This paper exposes a control architecture enabling rehabilitation of walking impaired patients with the lower-limb exoskeleton Atalante. Atalante's control system is modified to allow the patient to contribute to the walking motion through their efforts. Only the swing leg degree of freedom along the nominal path is relaxed. An online trajectory optimization checks that the muscle forces do not jeopardize stability. The optimization generates reference trajectories that satisfy several key constraints from the current point to the end of the step. One of the constraints requires that the center or pressure remains inside the support polygon, which ensures that the support leg subsystem successfully tracks the reference trajectory. As a result of the presented works, the robot provides a non-zero force in the direction of motion only when required, helping the patient go fast enough to maintain balance (or preventing him from going too fast). Experimental results are reported. They illustrate that variations of $\pm$50% of the duration of the step can be achieved in response to the patient's efforts and that many steps are achieved without falling. A video of the experiments can be viewed at https://youtu.be/_1A-2nLy5ZE

Data-Driven Observability Analysis for Nonlinear Stochastic Systems

Distinguishability and, by extension, observability are key properties of dynamical systems. Establishing these properties is challenging, especially when no analytical model is available and they are to be inferred directly from measurement data. The presence of noise further complicates this analysis, as standard notions of distinguishability are tailored to deterministic systems. We build on distributional distinguishability, which extends the deterministic notion by comparing distributions of outputs of stochastic systems. We first show that both concepts are equivalent for a class of systems that includes linear systems. We then present a method to assess and quantify distributional distinguishability from output data. Specifically, our quantification measures how much data is required to tell apart two initial states, inducing a continuous spectrum of distinguishability. We propose a statistical test to determine a threshold above which two states can be considered distinguishable with high confidence. We illustrate these tools by computing distinguishability maps over the state space in simulation, then leverage the test to compare sensor configurations on hardware.

Learning dynamics from partial observations with structured neural ODEs

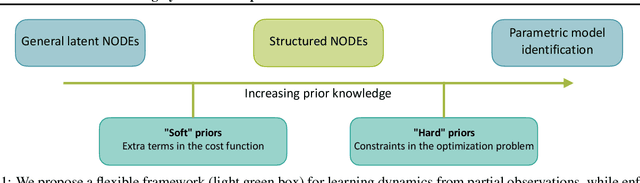
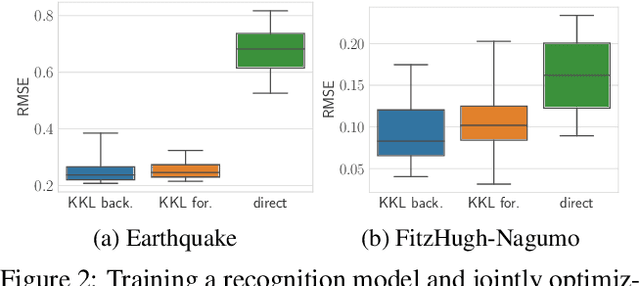
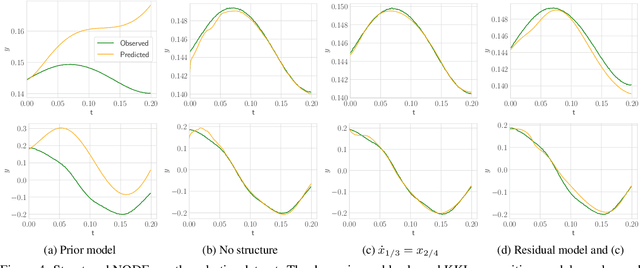
Identifying dynamical systems from experimental data is a notably difficult task. Prior knowledge generally helps, but the extent of this knowledge varies with the application, and customized models are often needed. We propose a flexible framework to incorporate a broad spectrum of physical insight into neural ODE-based system identification, giving physical interpretability to the resulting latent space. This insight is either enforced through hard constraints in the optimization problem or added in its cost function. In order to link the partial and possibly noisy observations to the latent state, we rely on tools from nonlinear observer theory to build a recognition model. We demonstrate the performance of the proposed approach on numerical simulations and on an experimental dataset from a robotic exoskeleton.