Explainability as statistical inference

A wide variety of model explanation approaches have been proposed in recent years, all guided by very different rationales and heuristics. In this paper, we take a new route and cast interpretability as a statistical inference problem. We propose a general deep probabilistic model designed to produce interpretable predictions. The model parameters can be learned via maximum likelihood, and the method can be adapted to any predictor network architecture and any type of prediction problem. Our method is a case of amortized interpretability models, where a neural network is used as a selector to allow for fast interpretation at inference time. Several popular interpretability methods are shown to be particular cases of regularised maximum likelihood for our general model. We propose new datasets with ground truth selection which allow for the evaluation of the features importance map. Using these datasets, we show experimentally that using multiple imputation provides more reasonable interpretations.

Generalised Mutual Information for Discriminative Clustering

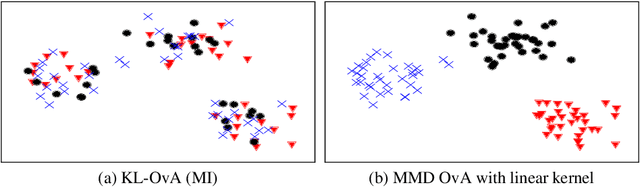
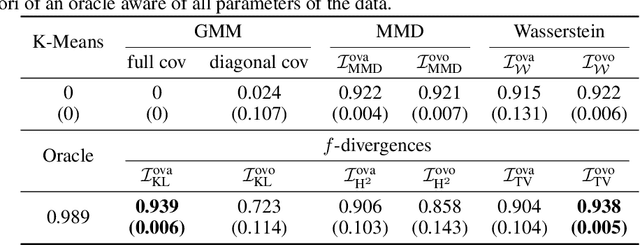
In the last decade, recent successes in deep clustering majorly involved the mutual information (MI) as an unsupervised objective for training neural networks with increasing regularisations. While the quality of the regularisations have been largely discussed for improvements, little attention has been dedicated to the relevance of MI as a clustering objective. In this paper, we first highlight how the maximisation of MI does not lead to satisfying clusters. We identified the Kullback-Leibler divergence as the main reason of this behaviour. Hence, we generalise the mutual information by changing its core distance, introducing the generalised mutual information (GEMINI): a set of metrics for unsupervised neural network training. Unlike MI, some GEMINIs do not require regularisations when training. Some of these metrics are geometry-aware thanks to distances or kernels in the data space. Finally, we highlight that GEMINIs can automatically select a relevant number of clusters, a property that has been little studied in deep clustering context where the number of clusters is a priori unknown.

A Multi-stage deep architecture for summary generation of soccer videos

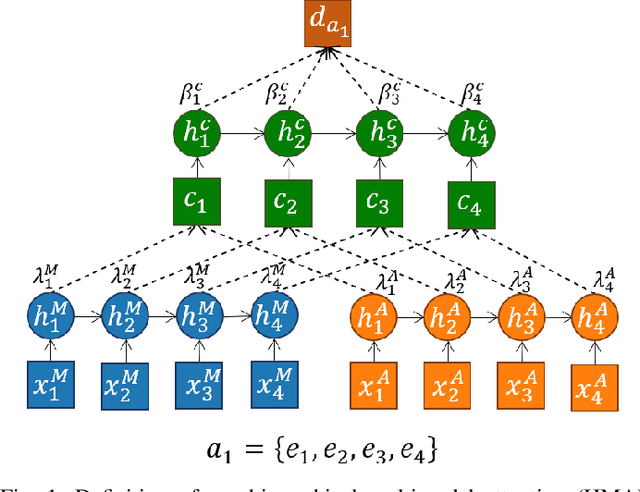
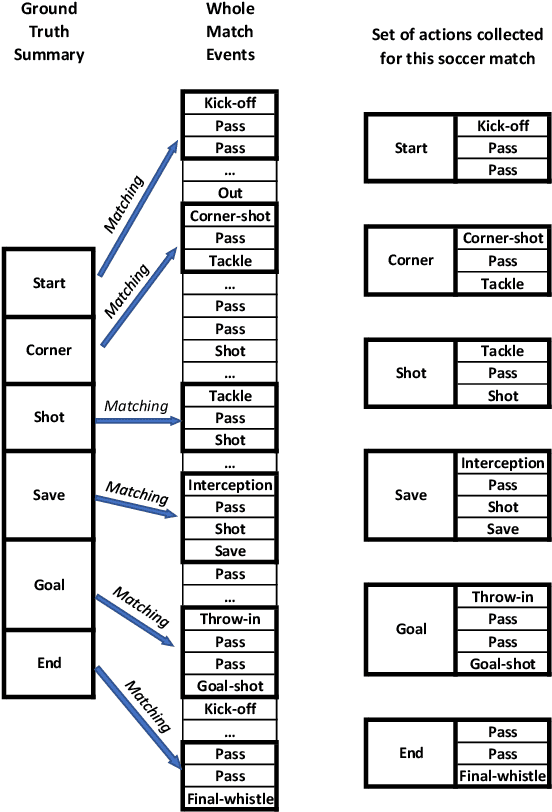
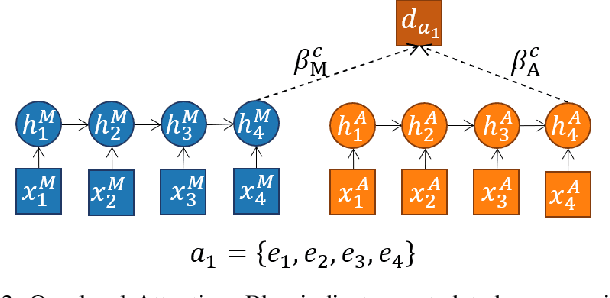
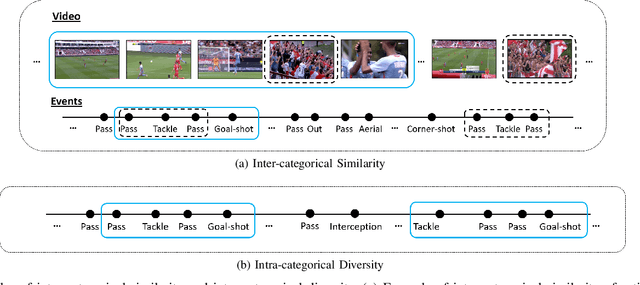
Video content is present in an ever-increasing number of fields, both scientific and commercial. Sports, particularly soccer, is one of the industries that has invested the most in the field of video analytics, due to the massive popularity of the game and the emergence of new markets. Previous state-of-the-art methods on soccer matches video summarization rely on handcrafted heuristics to generate summaries which are poorly generalizable, but these works have yet proven that multiple modalities help detect the best actions of the game. On the other hand, machine learning models with higher generalization potential have entered the field of summarization of general-purpose videos, offering several deep learning approaches. However, most of them exploit content specificities that are not appropriate for sport whole-match videos. Although video content has been for many years the main source for automatizing knowledge extraction in soccer, the data that records all the events happening on the field has become lately very important in sports analytics, since this event data provides richer context information and requires less processing. We propose a method to generate the summary of a soccer match exploiting both the audio and the event metadata. The results show that our method can detect the actions of the match, identify which of these actions should belong to the summary and then propose multiple candidate summaries which are similar enough but with relevant variability to provide different options to the final editor. Furthermore, we show the generalization capability of our work since it can transfer knowledge between datasets from different broadcasting companies, different competitions, acquired in different conditions, and corresponding to summaries of different lengths

Don't fear the unlabelled: safe deep semi-supervised learning via simple debiasing

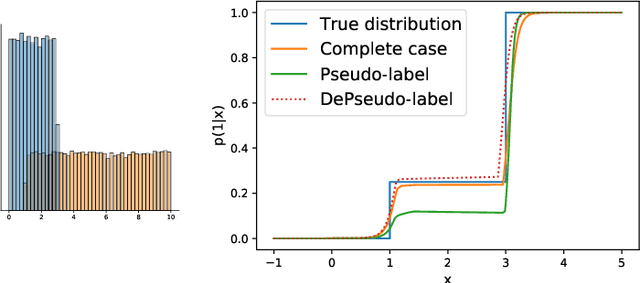
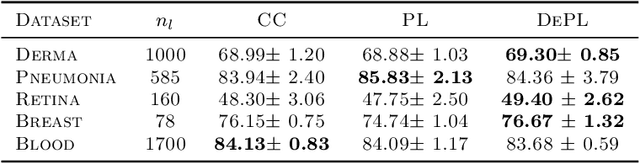
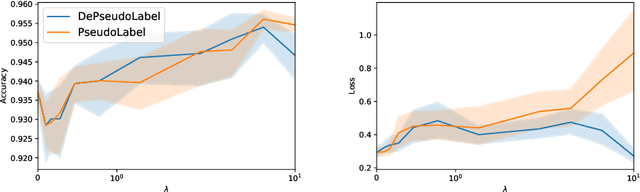
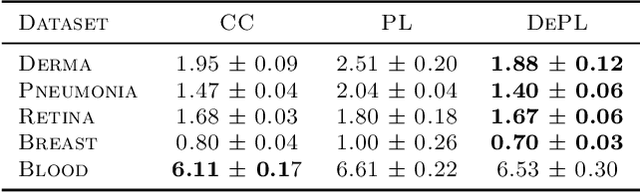
Semi supervised learning (SSL) provides an effective means of leveraging unlabelled data to improve a model's performance. Even though the domain has received a considerable amount of attention in the past years, most methods present the common drawback of being unsafe. By safeness we mean the quality of not degrading a fully supervised model when including unlabelled data. Our starting point is to notice that the estimate of the risk that most discriminative SSL methods minimise is biased, even asymptotically. This bias makes these techniques untrustable without a proper validation set, but we propose a simple way of removing the bias. Our debiasing approach is straightforward to implement, and applicable to most deep SSL methods. We provide simple theoretical guarantees on the safeness of these modified methods, without having to rely on the strong assumptions on the data distribution that SSL theory usually requires. We evaluate debiased versions of different existing SSL methods and show that debiasing can compete with classic deep SSL techniques in various classic settings and even performs well when traditional SSL fails.

Model-agnostic out-of-distribution detection using combined statistical tests

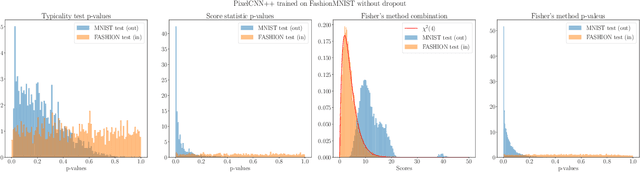
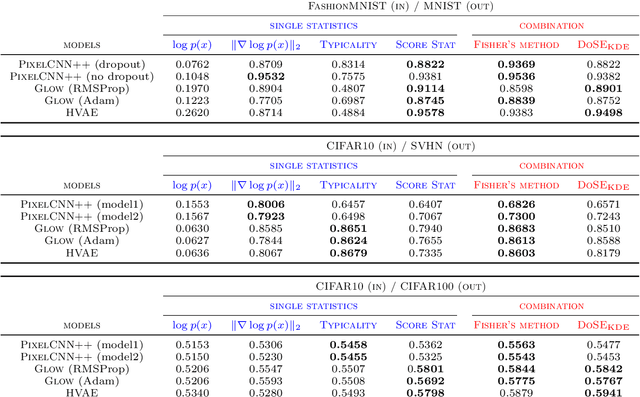
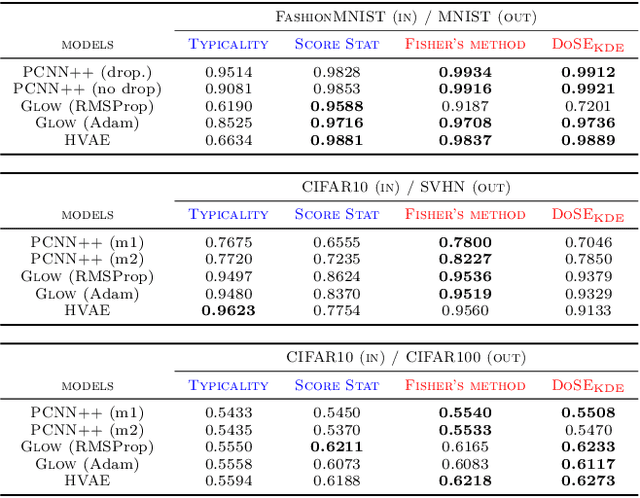
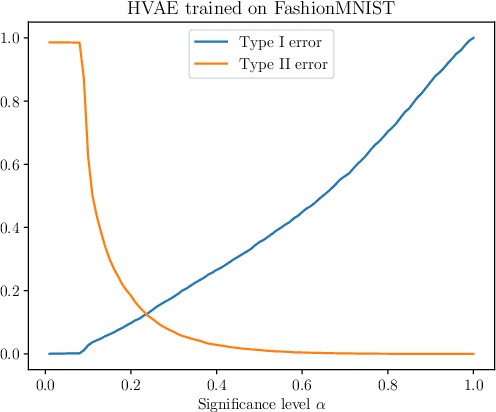
We present simple methods for out-of-distribution detection using a trained generative model. These techniques, based on classical statistical tests, are model-agnostic in the sense that they can be applied to any differentiable generative model. The idea is to combine a classical parametric test (Rao's score test) with the recently introduced typicality test. These two test statistics are both theoretically well-founded and exploit different sources of information based on the likelihood for the typicality test and its gradient for the score test. We show that combining them using Fisher's method overall leads to a more accurate out-of-distribution test. We also discuss the benefits of casting out-of-distribution detection as a statistical testing problem, noting in particular that false positive rate control can be valuable for practical out-of-distribution detection. Despite their simplicity and generality, these methods can be competitive with model-specific out-of-distribution detection algorithms without any assumptions on the out-distribution.

Uphill Roads to Variational Tightness: Monotonicity and Monte Carlo Objectives

We revisit the theory of importance weighted variational inference (IWVI), a promising strategy for learning latent variable models. IWVI uses new variational bounds, known as Monte Carlo objectives (MCOs), obtained by replacing intractable integrals by Monte Carlo estimates -- usually simply obtained via importance sampling. Burda, Grosse and Salakhutdinov (2016) showed that increasing the number of importance samples provably tightens the gap between the bound and the likelihood. Inspired by this simple monotonicity theorem, we present a series of nonasymptotic results that link properties of Monte Carlo estimates to tightness of MCOs. We challenge the rationale that smaller Monte Carlo variance leads to better bounds. We confirm theoretically the empirical findings of several recent papers by showing that, in a precise sense, negative correlation reduces the variational gap. We also generalise the original monotonicity theorem by considering non-uniform weights. We discuss several practical consequences of our theoretical results. Our work borrows many ideas and results from the theory of stochastic orders.

Tensor decomposition for learning Gaussian mixtures from moments

In data processing and machine learning, an important challenge is to recover and exploit models that can represent accurately the data. We consider the problem of recovering Gaussian mixture models from datasets. We investigate symmetric tensor decomposition methods for tackling this problem, where the tensor is built from empirical moments of the data distribution. We consider identifiable tensors, which have a unique decomposition, showing that moment tensors built from spherical Gaussian mixtures have this property. We prove that symmetric tensors with interpolation degree strictly less than half their order are identifiable and we present an algorithm, based on simple linear algebra operations, to compute their decomposition. Illustrative experimentations show the impact of the tensor decomposition method for recovering Gaussian mixtures, in comparison with other state-of-the-art approaches.

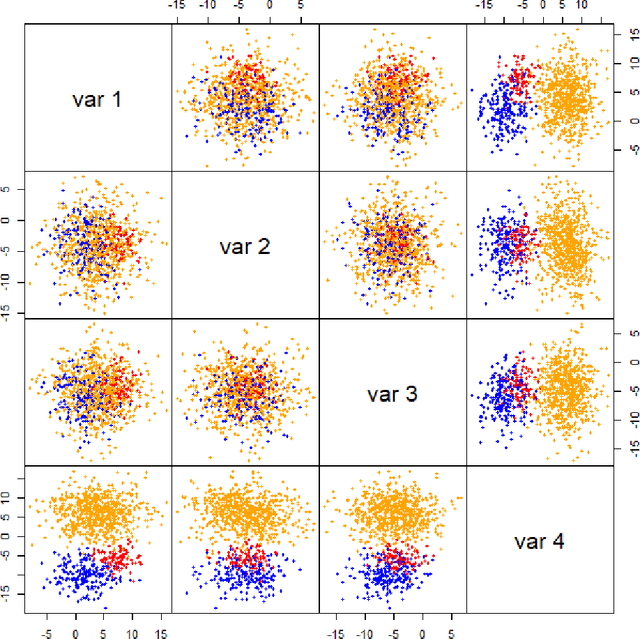
Unobserved classes and extra variables in high-dimensional discriminant analysis

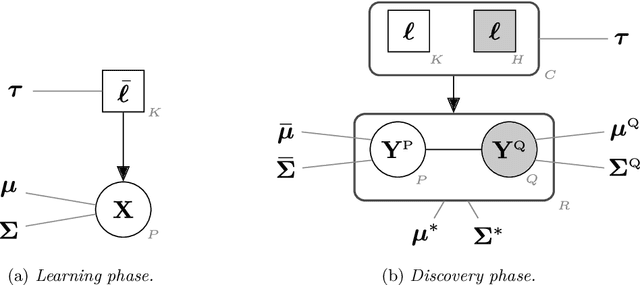
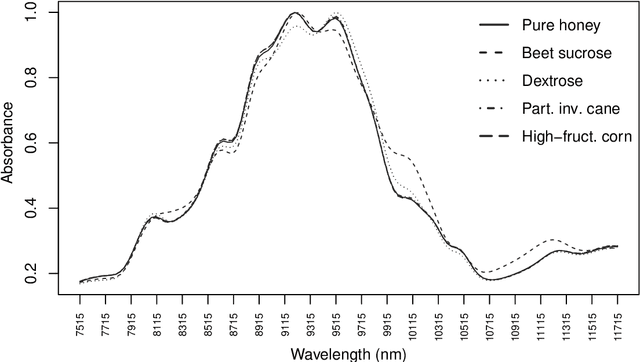
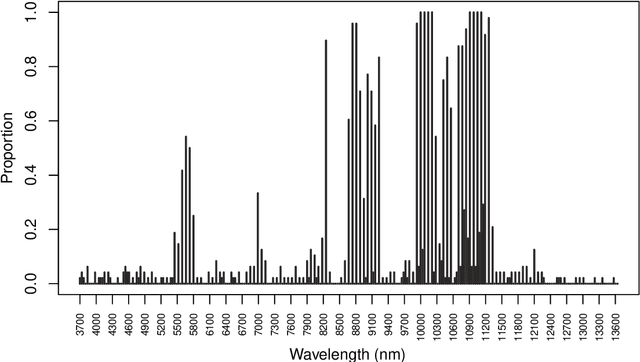
In supervised classification problems, the test set may contain data points belonging to classes not observed in the learning phase. Moreover, the same units in the test data may be measured on a set of additional variables recorded at a subsequent stage with respect to when the learning sample was collected. In this situation, the classifier built in the learning phase needs to adapt to handle potential unknown classes and the extra dimensions. We introduce a model-based discriminant approach, Dimension-Adaptive Mixture Discriminant Analysis (D-AMDA), which can detect unobserved classes and adapt to the increasing dimensionality. Model estimation is carried out via a full inductive approach based on an EM algorithm. The method is then embedded in a more general framework for adaptive variable selection and classification suitable for data of large dimensions. A simulation study and an artificial experiment related to classification of adulterated honey samples are used to validate the ability of the proposed framework to deal with complex situations.

not-MIWAE: Deep Generative Modelling with Missing not at Random Data

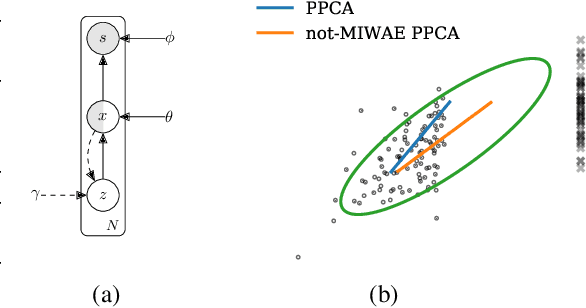
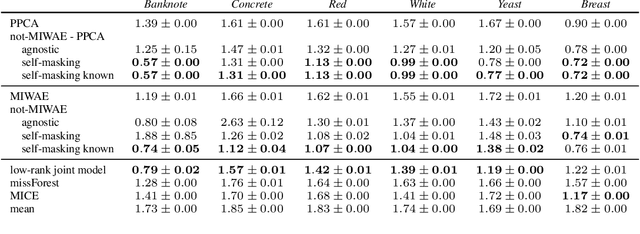
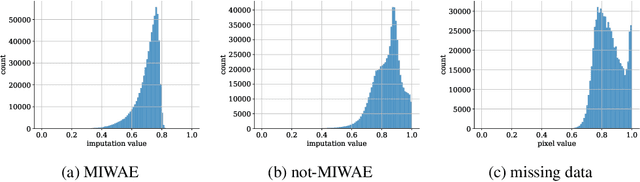
When a missing process depends on the missing values themselves, it needs to be explicitly modelled and taken into account while doing likelihood-based inference. We present an approach for building and fitting deep latent variable models (DLVMs) in cases where the missing process is dependent on the missing data. Specifically, a deep neural network enables us to flexibly model the conditional distribution of the missingness pattern given the data. This allows for incorporating prior information about the type of missingness (e.g. self-censoring) into the model. Our inference technique, based on importance-weighted variational inference, involves maximising a lower bound of the joint likelihood. Stochastic gradients of the bound are obtained by using the reparameterisation trick both in latent space and data space. We show on various kinds of data sets and missingness patterns that explicitly modelling the missing process can be invaluable.

Partially Exchangeable Networks and Architectures for Learning Summary Statistics in Approximate Bayesian Computation

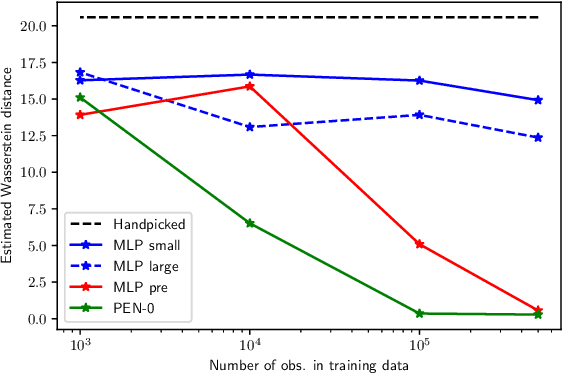
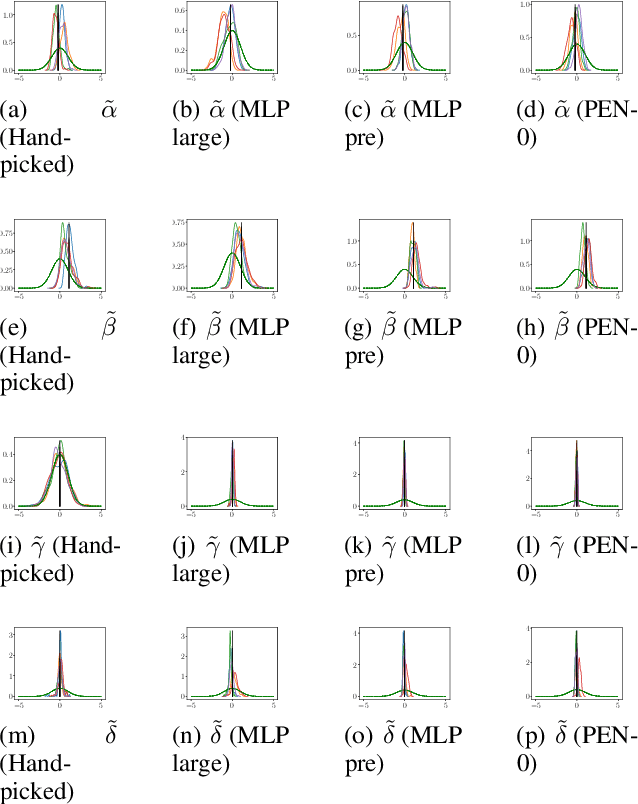
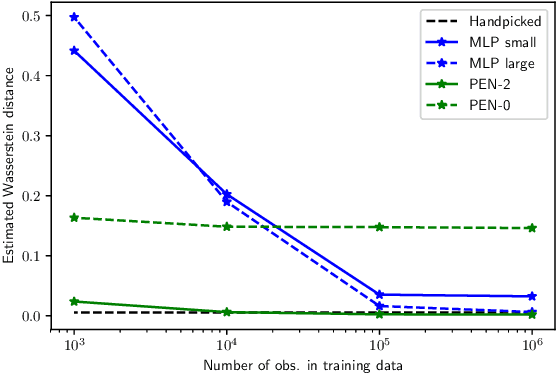
We present a novel family of deep neural architectures, named partially exchangeable networks (PENs) that leverage probabilistic symmetries. By design, PENs are invariant to block-switch transformations, which characterize the partial exchangeability properties of conditionally Markovian processes. Moreover, we show that any block-switch invariant function has a PEN-like representation. The DeepSets architecture is a special case of PEN and we can therefore also target fully exchangeable data. We employ PENs to learn summary statistics in approximate Bayesian computation (ABC). When comparing PENs to previous deep learning methods for learning summary statistics, our results are highly competitive, both considering time series and static models. Indeed, PENs provide more reliable posterior samples even when using less training data.