not-MIWAE: Deep Generative Modelling with Missing not at Random Data

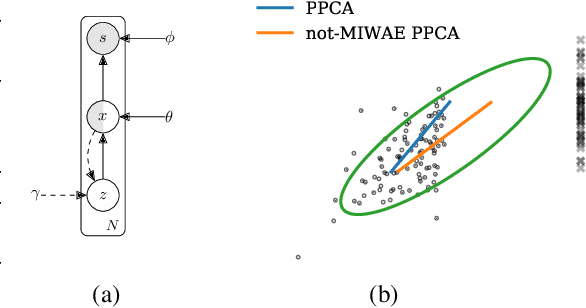
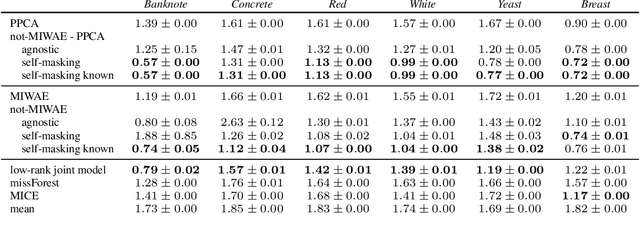
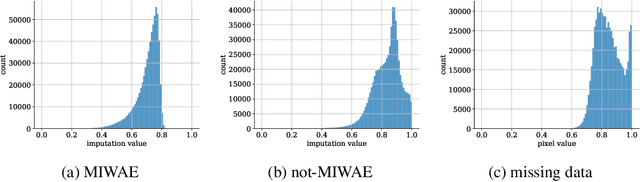
When a missing process depends on the missing values themselves, it needs to be explicitly modelled and taken into account while doing likelihood-based inference. We present an approach for building and fitting deep latent variable models (DLVMs) in cases where the missing process is dependent on the missing data. Specifically, a deep neural network enables us to flexibly model the conditional distribution of the missingness pattern given the data. This allows for incorporating prior information about the type of missingness (e.g. self-censoring) into the model. Our inference technique, based on importance-weighted variational inference, involves maximising a lower bound of the joint likelihood. Stochastic gradients of the bound are obtained by using the reparameterisation trick both in latent space and data space. We show on various kinds of data sets and missingness patterns that explicitly modelling the missing process can be invaluable.

Phase transition in PCA with missing data: Reduced signal-to-noise ratio, not sample size!

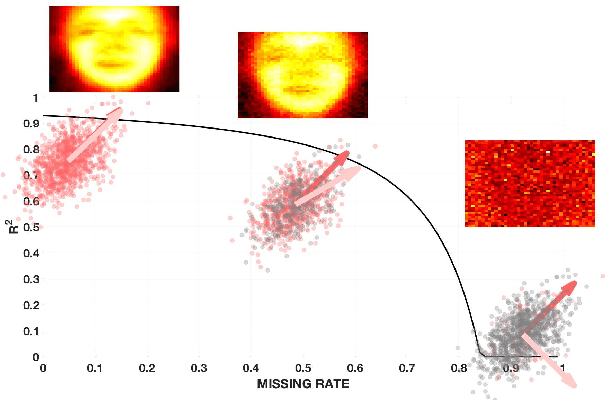
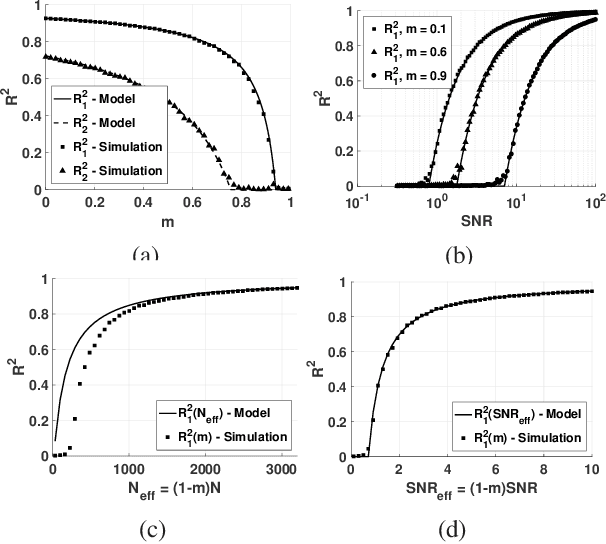
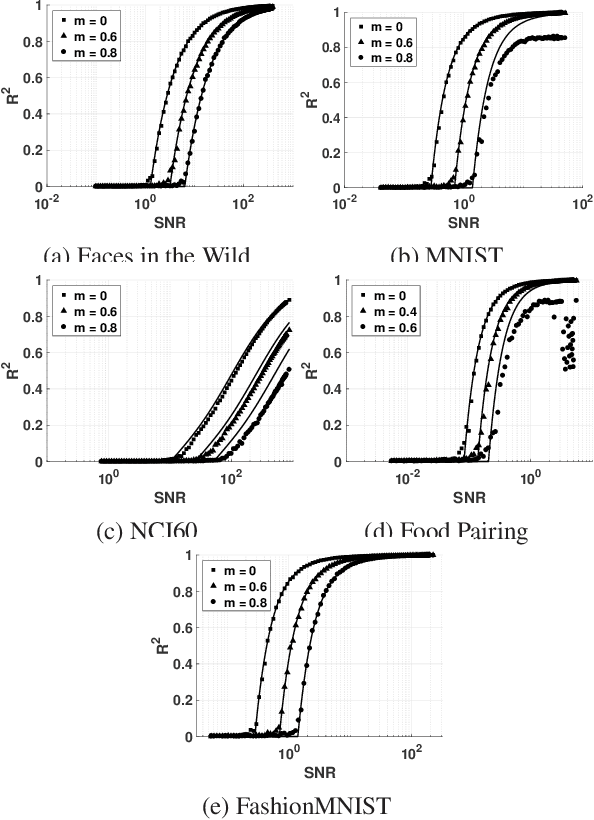
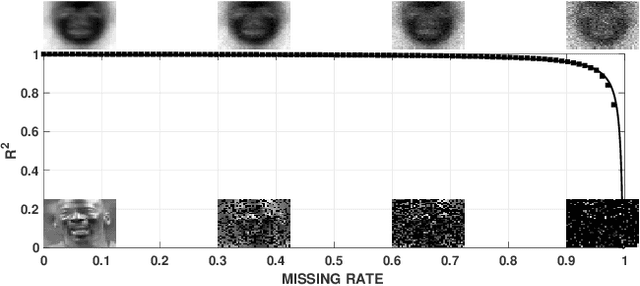
How does missing data affect our ability to learn signal structures? It has been shown that learning signal structure in terms of principal components is dependent on the ratio of sample size and dimensionality and that a critical number of observations is needed before learning starts (Biehl and Mietzner, 1993). Here we generalize this analysis to include missing data. Probabilistic principal component analysis is regularly used for estimating signal structures in datasets with missing data. Our analytic result suggests that the effect of missing data is to effectively reduce signal-to-noise ratio rather than - as generally believed - to reduce sample size. The theory predicts a phase transition in the learning curves and this is indeed found both in simulation data and in real datasets.