Computing the Reachability Value of Posterior-Deterministic POMDPs

Partially observable Markov decision processes (POMDPs) are a fundamental model for sequential decision-making under uncertainty. However, many verification and synthesis problems for POMDPs are undecidable or intractable. Most prominently, the seminal result of Madani et al. (2003) states that there is no algorithm that, given a POMDP and a set of target states, can compute the maximal probability of reaching the target states, or even approximate it up to a non-trivial constant. This is in stark contrast to fully observable Markov decision processes (MDPs), where the reachability value can be computed in polynomial time. In this work, we introduce posterior-deterministic POMDPs, a novel class of POMDPs. Our main technical contribution is to show that for posterior-deterministic POMDPs, the maximal probability of reaching a given set of states can be approximated up to arbitrary precision. A POMDP is posterior-deterministic if the next state can be uniquely determined by the current state, the action taken, and the observation received. While the actual state is generally uncertain in POMDPs, the posterior-deterministic property tells us that once the true state is known it remains known forever. This simple and natural definition includes all MDPs and captures classical non-trivial examples such as the Tiger POMDP (Kaelbling et al. 1998), making it one of the largest known classes of POMDPs for which the reachability value can be approximated.

Revelations: A Decidable Class of POMDPs with Omega-Regular Objectives

Partially observable Markov decision processes (POMDPs) form a prominent model for uncertainty in sequential decision making. We are interested in constructing algorithms with theoretical guarantees to determine whether the agent has a strategy ensuring a given specification with probability 1. This well-studied problem is known to be undecidable already for very simple omega-regular objectives, because of the difficulty of reasoning on uncertain events. We introduce a revelation mechanism which restricts information loss by requiring that almost surely the agent has eventually full information of the current state. Our main technical results are to construct exact algorithms for two classes of POMDPs called weakly and strongly revealing. Importantly, the decidable cases reduce to the analysis of a finite belief-support Markov decision process. This yields a conceptually simple and exact algorithm for a large class of POMDPs.

Games Where You Can Play Optimally with Finite Memory

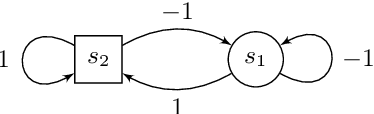
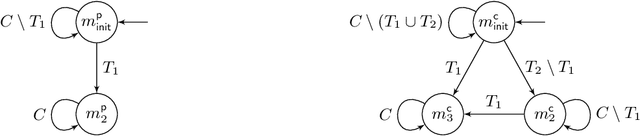
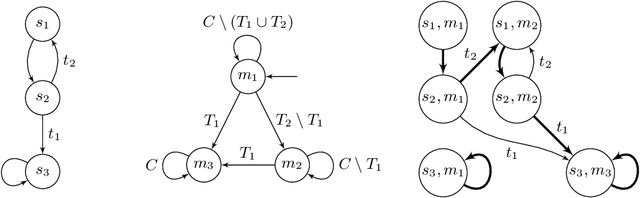
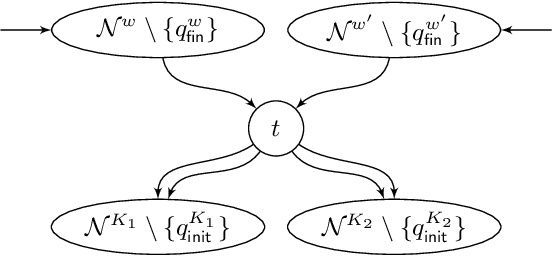
For decades, two-player (antagonistic) games on graphs have been a framework of choice for many important problems in theoretical computer science. A notorious one is controller synthesis, which can be rephrased through the game-theoretic metaphor as the quest for a winning strategy of the system in a game against its antagonistic environment. Depending on the specification, optimal strategies might be simple or quite complex, for example having to use (possibly infinite) memory. Hence, research strives to understand which settings allow for simple strategies. In 2005, Gimbert and Zielonka provided a complete characterization of preference relations (a formal framework to model specifications and game objectives) that admit memoryless optimal strategies for both players. In the last fifteen years however, practical applications have driven the community toward games with complex or multiple objectives, where memory --- finite or infinite --- is almost always required. Despite much effort, the exact frontiers of the class of preference relations that admit finite-memory optimal strategies still elude us. In this work, we establish a complete characterization of preference relations that admit optimal strategies using arena-independent finite memory, generalizing the work of Gimbert and Zielonka to the finite-memory case. We also prove an equivalent to their celebrated corollary of utmost practical interest: if both players have optimal (arena-independent-)finite-memory strategies in all one-player games, then it is also the case in all two-player games. Finally, we pinpoint the boundaries of our results with regard to the literature: our work completely covers the case of arena-independent memory (e.g., multiple parity objectives, lower- and upper-bounded energy objectives), and paves the way to the arena-dependent case (e.g., multiple lower-bounded energy objectives).