Stochastic Training is Not Necessary for Generalization

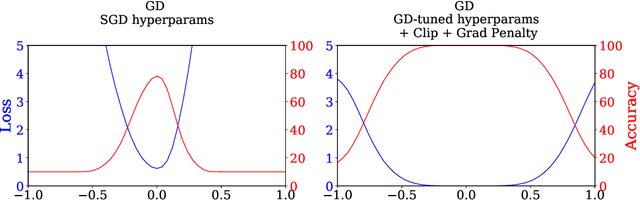
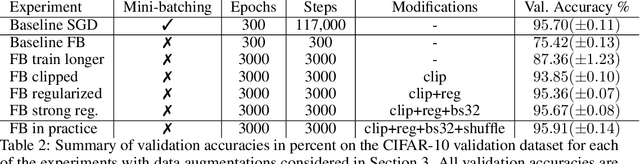
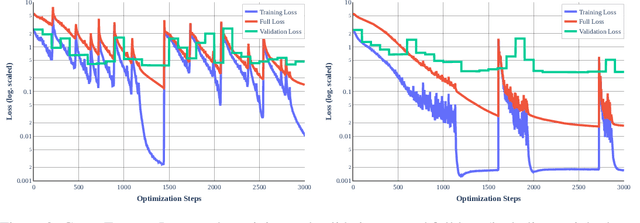
It is widely believed that the implicit regularization of stochastic gradient descent (SGD) is fundamental to the impressive generalization behavior we observe in neural networks. In this work, we demonstrate that non-stochastic full-batch training can achieve strong performance on CIFAR-10 that is on-par with SGD, using modern architectures in settings with and without data augmentation. To this end, we utilize modified hyperparameters and show that the implicit regularization of SGD can be completely replaced with explicit regularization. This strongly suggests that theories that rely heavily on properties of stochastic sampling to explain generalization are incomplete, as strong generalization behavior is still observed in the absence of stochastic sampling. Fundamentally, deep learning can succeed without stochasticity. Our observations further indicate that the perceived difficulty of full-batch training is largely the result of its optimization properties and the disproportionate time and effort spent by the ML community tuning optimizers and hyperparameters for small-batch training.

Sliced-Wasserstein Autoencoder: An Embarrassingly Simple Generative Model

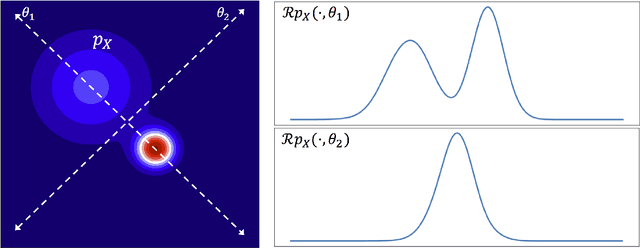
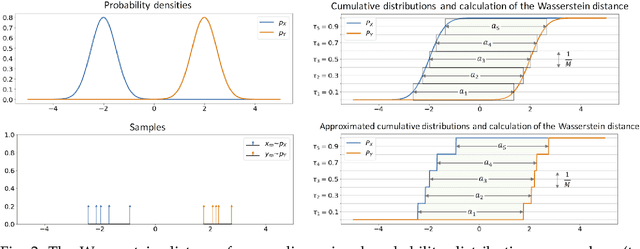
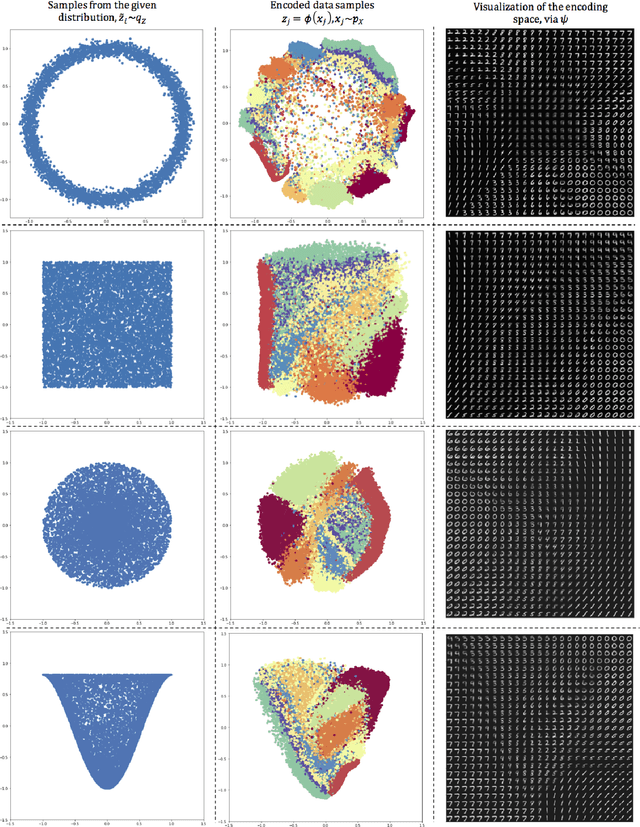
In this paper we study generative modeling via autoencoders while using the elegant geometric properties of the optimal transport (OT) problem and the Wasserstein distances. We introduce Sliced-Wasserstein Autoencoders (SWAE), which are generative models that enable one to shape the distribution of the latent space into any samplable probability distribution without the need for training an adversarial network or defining a closed-form for the distribution. In short, we regularize the autoencoder loss with the sliced-Wasserstein distance between the distribution of the encoded training samples and a predefined samplable distribution. We show that the proposed formulation has an efficient numerical solution that provides similar capabilities to Wasserstein Autoencoders (WAE) and Variational Autoencoders (VAE), while benefiting from an embarrassingly simple implementation.