Limiting fluctuation and trajectorial stability of multilayer neural networks with mean field training

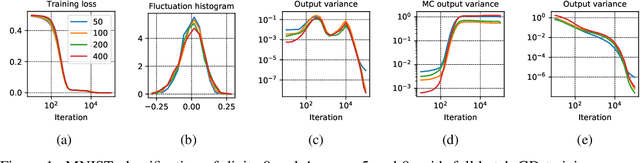
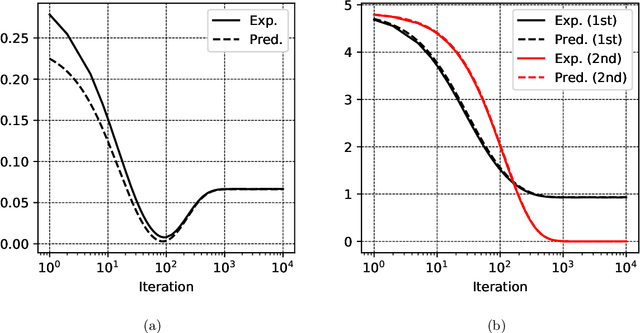
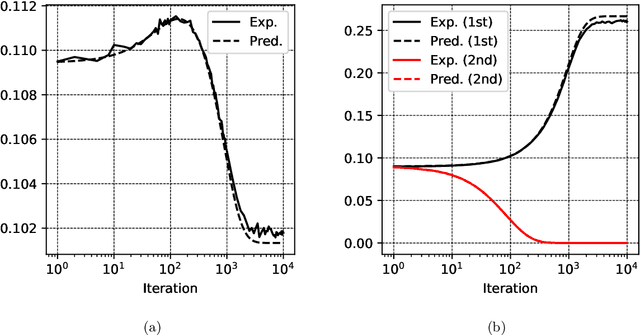
The mean field (MF) theory of multilayer neural networks centers around a particular infinite-width scaling, where the learning dynamics is closely tracked by the MF limit. A random fluctuation around this infinite-width limit is expected from a large-width expansion to the next order. This fluctuation has been studied only in shallow networks, where previous works employ heavily technical notions or additional formulation ideas amenable only to that case. Treatment of the multilayer case has been missing, with the chief difficulty in finding a formulation that captures the stochastic dependency across not only time but also depth. In this work, we initiate the study of the fluctuation in the case of multilayer networks, at any network depth. Leveraging on the neuronal embedding framework recently introduced by Nguyen and Pham, we systematically derive a system of dynamical equations, called the second-order MF limit, that captures the limiting fluctuation distribution. We demonstrate through the framework the complex interaction among neurons in this second-order MF limit, the stochasticity with cross-layer dependency and the nonlinear time evolution inherent in the limiting fluctuation. A limit theorem is proven to relate quantitatively this limit to the fluctuation of large-width networks. We apply the result to show a stability property of gradient descent MF training: in the large-width regime, along the training trajectory, it progressively biases towards a solution with "minimal fluctuation" (in fact, vanishing fluctuation) in the learned output function, even after the network has been initialized at or has converged (sufficiently fast) to a global optimum. This extends a similar phenomenon previously shown only for shallow networks with a squared loss in the ERM setting, to multilayer networks with a loss function that is not necessarily convex in a more general setting.

Global Convergence of Three-layer Neural Networks in the Mean Field Regime

In the mean field regime, neural networks are appropriately scaled so that as the width tends to infinity, the learning dynamics tends to a nonlinear and nontrivial dynamical limit, known as the mean field limit. This lends a way to study large-width neural networks via analyzing the mean field limit. Recent works have successfully applied such analysis to two-layer networks and provided global convergence guarantees. The extension to multilayer ones however has been a highly challenging puzzle, and little is known about the optimization efficiency in the mean field regime when there are more than two layers. In this work, we prove a global convergence result for unregularized feedforward three-layer networks in the mean field regime. We first develop a rigorous framework to establish the mean field limit of three-layer networks under stochastic gradient descent training. To that end, we propose the idea of a \textit{neuronal embedding}, which comprises of a fixed probability space that encapsulates neural networks of arbitrary sizes. The identified mean field limit is then used to prove a global convergence guarantee under suitable regularity and convergence mode assumptions, which -- unlike previous works on two-layer networks -- does not rely critically on convexity. Underlying the result is a universal approximation property, natural of neural networks, which importantly is shown to hold at \textit{any} finite training time (not necessarily at convergence) via an algebraic topology argument.

Analysis of feature learning in weight-tied autoencoders via the mean field lens

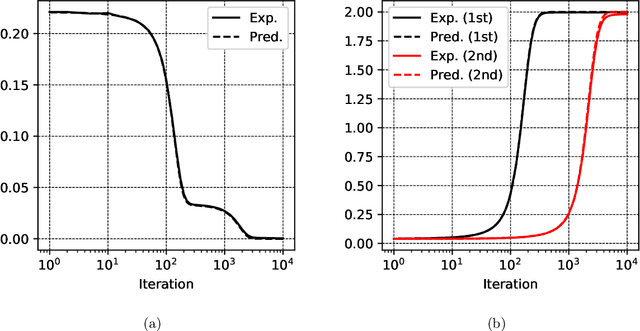
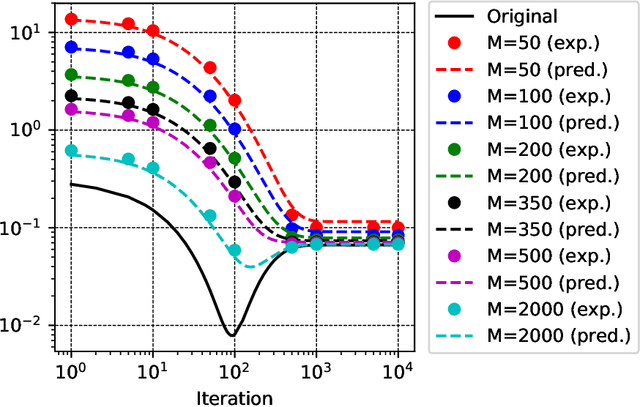
Autoencoders are among the earliest introduced nonlinear models for unsupervised learning. Although they are widely adopted beyond research, it has been a longstanding open problem to understand mathematically the feature extraction mechanism that trained nonlinear autoencoders provide. In this work, we make progress in this problem by analyzing a class of two-layer weight-tied nonlinear autoencoders in the mean field framework. Upon a suitable scaling, in the regime of a large number of neurons, the models trained with stochastic gradient descent are shown to admit a mean field limiting dynamics. This limiting description reveals an asymptotically precise picture of feature learning by these models: their training dynamics exhibit different phases that correspond to the learning of different principal subspaces of the data, with varying degrees of nonlinear shrinkage dependent on the $\ell_{2}$-regularization and stopping time. While we prove these results under an idealized assumption of (correlated) Gaussian data, experiments on real-life data demonstrate an interesting match with the theory. The autoencoder setup of interests poses a nontrivial mathematical challenge to proving these results. In this setup, the "Lipschitz" constants of the models grow with the data dimension $d$. Consequently an adaptation of previous analyses requires a number of neurons $N$ that is at least exponential in $d$. Our main technical contribution is a new argument which proves that the required $N$ is only polynomial in $d$. We conjecture that $N\gg d$ is sufficient and that $N$ is necessarily larger than a data-dependent intrinsic dimension, a behavior that is fundamentally different from previously studied setups.

A Note on the Global Convergence of Multilayer Neural Networks in the Mean Field Regime

In a recent work, we introduced a rigorous framework to describe the mean field limit of the gradient-based learning dynamics of multilayer neural networks, based on the idea of a neuronal embedding. There we also proved a global convergence guarantee for three-layer (as well as two-layer) networks using this framework. In this companion note, we point out that the insights in our previous work can be readily extended to prove a global convergence guarantee for multilayer networks of any depths. Unlike our previous three-layer global convergence guarantee that assumes i.i.d. initializations, our present result applies to a type of correlated initialization. This initialization allows to, at any finite training time, propagate a certain universal approximation property through the depth of the neural network. To achieve this effect, we introduce a bidirectional diversity condition.

A Rigorous Framework for the Mean Field Limit of Multilayer Neural Networks

We develop a mathematically rigorous framework for multilayer neural networks in the mean field regime. As the network's width increases, the network's learning trajectory is shown to be well captured by a meaningful and dynamically nonlinear limit (the \textit{mean field} limit), which is characterized by a system of ODEs. Our framework applies to a broad range of network architectures, learning dynamics and network initializations. Central to the framework is the new idea of a \textit{neuronal embedding}, which comprises of a non-evolving probability space that allows to embed neural networks of arbitrary widths. We demonstrate two applications of our framework. Firstly the framework gives a principled way to study the simplifying effects that independent and identically distributed initializations have on the mean field limit. Secondly we prove a global convergence guarantee for two-layer and three-layer networks. Unlike previous works that rely on convexity, our result requires a certain universal approximation property, which is a distinctive feature of infinite-width neural networks. To the best of our knowledge, this is the first time global convergence is established for neural networks of more than two layers in the mean field regime.

Mean Field Limit of the Learning Dynamics of Multilayer Neural Networks

Can multilayer neural networks -- typically constructed as highly complex structures with many nonlinearly activated neurons across layers -- behave in a non-trivial way that yet simplifies away a major part of their complexities? In this work, we uncover a phenomenon in which the behavior of these complex networks -- under suitable scalings and stochastic gradient descent dynamics -- becomes independent of the number of neurons as this number grows sufficiently large. We develop a formalism in which this many-neurons limiting behavior is captured by a set of equations, thereby exposing a previously unknown operating regime of these networks. While the current pursuit is mathematically non-rigorous, it is complemented with several experiments that validate the existence of this behavior.

A Mean Field View of the Landscape of Two-Layers Neural Networks

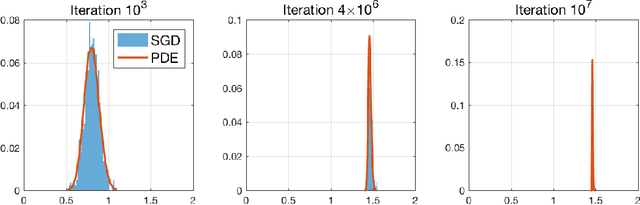
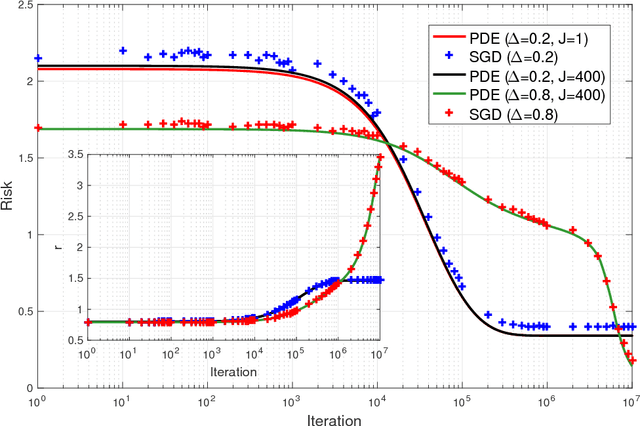
Multi-layer neural networks are among the most powerful models in machine learning, yet the fundamental reasons for this success defy mathematical understanding. Learning a neural network requires to optimize a non-convex high-dimensional objective (risk function), a problem which is usually attacked using stochastic gradient descent (SGD). Does SGD converge to a global optimum of the risk or only to a local optimum? In the first case, does this happen because local minima are absent, or because SGD somehow avoids them? In the second, why do local minima reached by SGD have good generalization properties? In this paper we consider a simple case, namely two-layers neural networks, and prove that -in a suitable scaling limit- SGD dynamics is captured by a certain non-linear partial differential equation (PDE) that we call distributional dynamics (DD). We then consider several specific examples, and show how DD can be used to prove convergence of SGD to networks with nearly ideal generalization error. This description allows to 'average-out' some of the complexities of the landscape of neural networks, and can be used to prove a general convergence result for noisy SGD.