Artificial Intelligence-Informed Handheld Breast Ultrasound for Screening: A Systematic Review of Diagnostic Test Accuracy

Background. Breast cancer screening programs using mammography have led to significant mortality reduction in high-income countries. However, many low- and middle-income countries lack resources for mammographic screening. Handheld breast ultrasound (BUS) is a low-cost alternative but requires substantial training. Artificial intelligence (AI) enabled BUS may aid in both the detection (perception) and classification (interpretation) of breast cancer. Materials and Methods. This review (CRD42023493053) is reported in accordance with the PRISMA (Preferred Reporting Items for Systematic Reviews and Meta-Analysis) and SWiM (Synthesis Without Meta-analysis) guidelines. PubMed and Google Scholar were searched from January 1, 2016 to December 12, 2023. A meta-analysis was not attempted. Studies are grouped according to their AI task type, application time, and AI task. Study quality is assessed using the QUality Assessment of Diagnostic Accuracy Studies-2 (QUADAS-2) tool. Results. Of 763 candidate studies, 314 total full texts were reviewed. 34 studies are included. The AI tasks of included studies are as follows: 1 frame selection, 6 detection, 11 segmentation, and 16 classification. In total, 5.7 million BUS images from over 185,000 patients were used for AI training or validation. A single study included a prospective testing set. 79% of studies were at high or unclear risk of bias. Conclusion. There has been encouraging development of AI for BUS. Despite studies demonstrating high performance across all identified tasks, the evidence supporting AI-enhanced BUS generally lacks robustness. High-quality model validation will be key to realizing the potential for AI-enhanced BUS in increasing access to screening in resource-limited environments.

Deep Learning Predicts Mammographic Breast Density in Clinical Breast Ultrasound Images

Background: Mammographic breast density, as defined by the American College of Radiology's Breast Imaging Reporting and Data System (BI-RADS), is one of the strongest risk factors for breast cancer, but is derived from mammographic images. Breast ultrasound (BUS) is an alternative breast cancer screening modality, particularly useful for early detection in low-resource, rural contexts. The purpose of this study was to explore an artificial intelligence (AI) model to predict BI-RADS mammographic breast density category from clinical, handheld BUS imaging. Methods: All data are sourced from the Hawaii and Pacific Islands Mammography Registry. We compared deep learning methods from BUS imaging, as well as machine learning models from image statistics alone. The use of AI-derived BUS density as a risk factor for breast cancer was then compared to clinical BI-RADS breast density while adjusting for age. The BUS data were split by individual into 70/20/10% groups for training, validation, and testing. Results: 405,120 clinical BUS images from 14.066 women were selected for inclusion in this study, resulting in 9.846 women for training (302,574 images), 2,813 for validation (11,223 images), and 1,406 for testing (4,042 images). On the held-out testing set, the strongest AI model achieves AUROC 0.854 predicting BI-RADS mammographic breast density from BUS imaging and outperforms all shallow machine learning methods based on image statistics. In cancer risk prediction, age-adjusted AI BUS breast density predicted 5-year breast cancer risk with 0.633 AUROC, as compared to 0.637 AUROC from age-adjusted clinical breast density. Conclusions: BI-RADS mammographic breast density can be estimated from BUS imaging with high accuracy using a deep learning model. Furthermore, we demonstrate that AI-derived BUS breast density is predictive of 5-year breast cancer risk in our population.

Neural Surrogate HMC: Accelerated Hamiltonian Monte Carlo with a Neural Network Surrogate Likelihood

Bayesian Inference with Markov Chain Monte Carlo requires efficient computation of the likelihood function. In some scientific applications, the likelihood must be computed by numerically solving a partial differential equation, which can be prohibitively expensive. We demonstrate that some such problems can be made tractable by amortizing the computation with a surrogate likelihood function implemented by a neural network. We show that this has two additional benefits: reducing noise in the likelihood evaluations and providing fast gradient calculations. In experiments, the approach is applied to a model of heliospheric transport of galactic cosmic rays, where it enables efficient sampling from the posterior of latent parameters in the Parker equation.

BUSClean: Open-source software for breast ultrasound image pre-processing and knowledge extraction for medical AI

Development of artificial intelligence (AI) for medical imaging demands curation and cleaning of large-scale clinical datasets comprising hundreds of thousands of images. Some modalities, such as mammography, contain highly standardized imaging. In contrast, breast ultrasound imaging (BUS) can contain many irregularities not indicated by scan metadata, such as enhanced scan modes, sonographer annotations, or additional views. We present an open-source software solution for automatically processing clinical BUS datasets. The algorithm performs BUS scan filtering, cleaning, and knowledge extraction from sonographer annotations. Its modular design enables users to adapt it to new settings. Experiments on an internal testing dataset of 430 clinical BUS images achieve >95% sensitivity and >98% specificity in detecting every type of text annotation, >98% sensitivity and specificity in detecting scans with blood flow highlighting, alternative scan modes, or invalid scans. A case study on a completely external, public dataset of BUS scans found that BUSClean identified text annotations and scans with blood flow highlighting with 88.6% and 90.9% sensitivity and 98.3% and 99.9% specificity, respectively. Adaptation of the lesion caliper detection method to account for a type of caliper specific to the case study demonstrates intended use of BUSClean in new data distributions and improved performance in lesion caliper detection from 43.3% and 93.3% out-of-the-box to 92.1% and 92.3% sensitivity and specificity, respectively. Source code, example notebooks, and sample data are available at https://github.com/hawaii-ai/bus-cleaning.

Learning a Clinically-Relevant Concept Bottleneck for Lesion Detection in Breast Ultrasound

Detecting and classifying lesions in breast ultrasound images is a promising application of artificial intelligence (AI) for reducing the burden of cancer in regions with limited access to mammography. Such AI systems are more likely to be useful in a clinical setting if their predictions can be explained to a radiologist. This work proposes an explainable AI model that provides interpretable predictions using a standard lexicon from the American College of Radiology's Breast Imaging and Reporting Data System (BI-RADS). The model is a deep neural network featuring a concept bottleneck layer in which known BI-RADS features are predicted before making a final cancer classification. This enables radiologists to easily review the predictions of the AI system and potentially fix errors in real time by modifying the concept predictions. In experiments, a model is developed on 8,854 images from 994 women with expert annotations and histological cancer labels. The model outperforms state-of-the-art lesion detection frameworks with 48.9 average precision on the held-out testing set, and for cancer classification, concept intervention is shown to increase performance from 0.876 to 0.885 area under the receiver operating characteristic curve. Training and evaluation code is available at https://github.com/hawaii-ai/bus-cbm.

WV-Net: A foundation model for SAR WV-mode satellite imagery trained using contrastive self-supervised learning on 10 million images

The European Space Agency's Copernicus Sentinel-1 (S-1) mission is a constellation of C-band synthetic aperture radar (SAR) satellites that provide unprecedented monitoring of the world's oceans. S-1's wave mode (WV) captures 20x20 km image patches at 5 m pixel resolution and is unaffected by cloud cover or time-of-day. The mission's open data policy has made SAR data easily accessible for a range of applications, but the need for manual image annotations is a bottleneck that hinders the use of machine learning methods. This study uses nearly 10 million WV-mode images and contrastive self-supervised learning to train a semantic embedding model called WV-Net. In multiple downstream tasks, WV-Net outperforms a comparable model that was pre-trained on natural images (ImageNet) with supervised learning. Experiments show improvements for estimating wave height (0.50 vs 0.60 RMSE using linear probing), estimating near-surface air temperature (0.90 vs 0.97 RMSE), and performing multilabel-classification of geophysical and atmospheric phenomena (0.96 vs 0.95 micro-averaged AUROC). WV-Net embeddings are also superior in an unsupervised image-retrieval task and scale better in data-sparse settings. Together, these results demonstrate that WV-Net embeddings can support geophysical research by providing a convenient foundation model for a variety of data analysis and exploration tasks.

FishNet: Deep Neural Networks for Low-Cost Fish Stock Estimation

Fish stock assessment often involves manual fish counting by taxonomy specialists, which is both time-consuming and costly. We propose an automated computer vision system that performs both taxonomic classification and fish size estimation from images taken with a low-cost digital camera. The system first performs object detection and segmentation using a Mask R-CNN to identify individual fish from images containing multiple fish, possibly consisting of different species. Then each fish species is classified and the predicted length using separate machine learning models. These models are trained on a dataset of 50,000 hand-annotated images containing 163 different fish species, ranging in length from 10cm to 250cm. Evaluated on held-out test data, our system achieves a $92\%$ intersection over union on the fish segmentation task, a $89\%$ top-1 classification accuracy on single fish species classification, and a $2.3$~cm mean error on the fish length estimation task.

Diffusion Models for High-Resolution Solar Forecasts

Forecasting future weather and climate is inherently difficult. Machine learning offers new approaches to increase the accuracy and computational efficiency of forecasts, but current methods are unable to accurately model uncertainty in high-dimensional predictions. Score-based diffusion models offer a new approach to modeling probability distributions over many dependent variables, and in this work, we demonstrate how they provide probabilistic forecasts of weather and climate variables at unprecedented resolution, speed, and accuracy. We apply the technique to day-ahead solar irradiance forecasts by generating many samples from a diffusion model trained to super-resolve coarse-resolution numerical weather predictions to high-resolution weather satellite observations.

Tourbillon: a Physically Plausible Neural Architecture

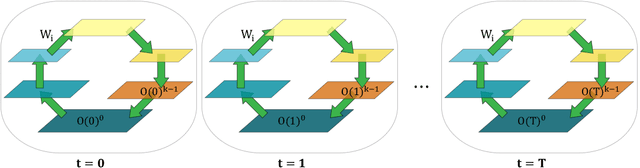
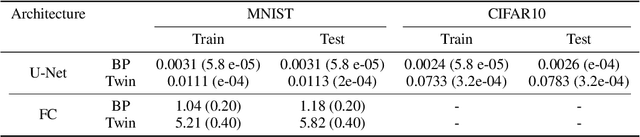
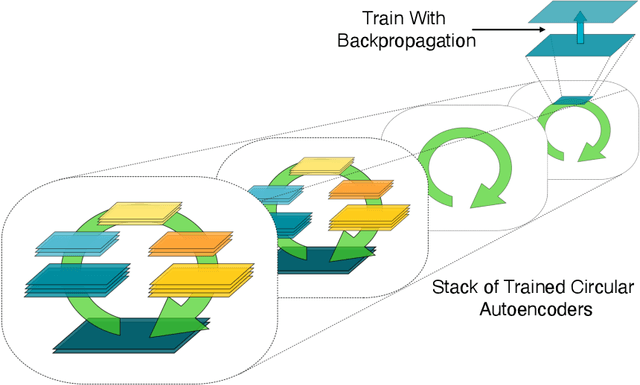
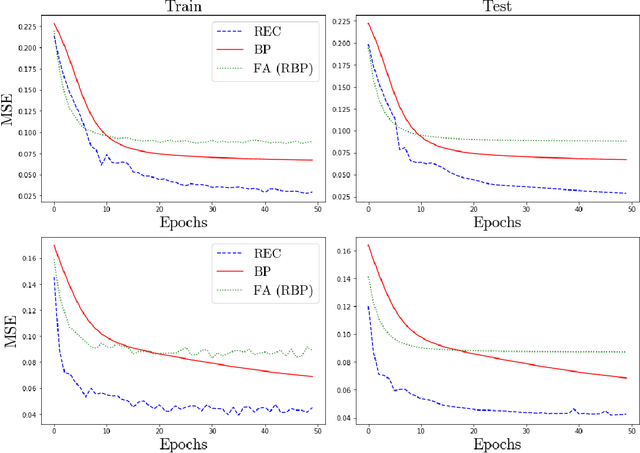
In a physical neural system, backpropagation is faced with a number of obstacles including: the need for labeled data, the violation of the locality learning principle, the need for symmetric connections, and the lack of modularity. Tourbillon is a new architecture that addresses all these limitations. At its core, it consists of a stack of circular autoencoders followed by an output layer. The circular autoencoders are trained in self-supervised mode by recirculation algorithms and the top layer in supervised mode by stochastic gradient descent, with the option of propagating error information through the entire stack using non-symmetric connections. While the Tourbillon architecture is meant primarily to address physical constraints, and not to improve current engineering applications of deep learning, we demonstrate its viability on standard benchmark datasets including MNIST, Fashion MNIST, and CIFAR10. We show that Tourbillon can achieve comparable performance to models trained with backpropagation and outperform models that are trained with other physically plausible algorithms, such as feedback alignment.

Sherpa: Robust Hyperparameter Optimization for Machine Learning

Sherpa is a hyperparameter optimization library for machine learning models. It is specifically designed for problems with computationally expensive, iterative function evaluations, such as the hyperparameter tuning of deep neural networks. With Sherpa, scientists can quickly optimize hyperparameters using a variety of powerful and interchangeable algorithms. Sherpa can be run on either a single machine or in parallel on a cluster. Finally, an interactive dashboard enables users to view the progress of models as they are trained, cancel trials, and explore which hyperparameter combinations are working best. Sherpa empowers machine learning practitioners by automating the more tedious aspects of model tuning. Its source code and documentation are available at https://github.com/sherpa-ai/sherpa.