Embedding Logical Queries on Knowledge Graphs

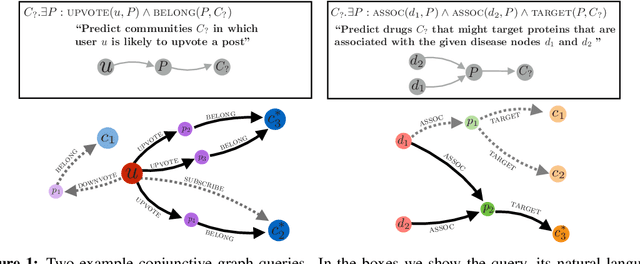
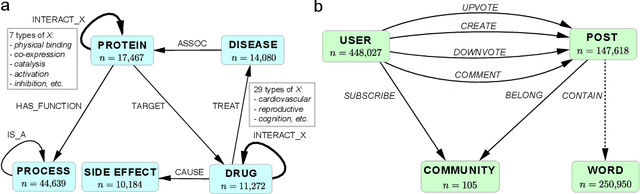
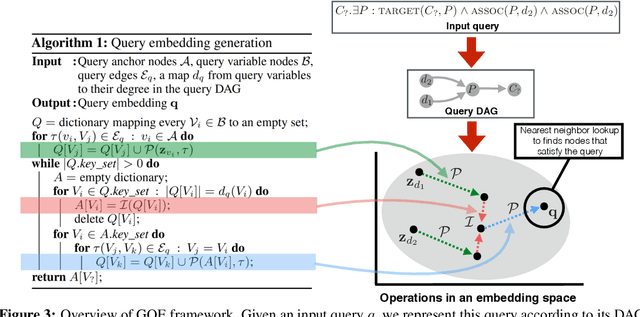
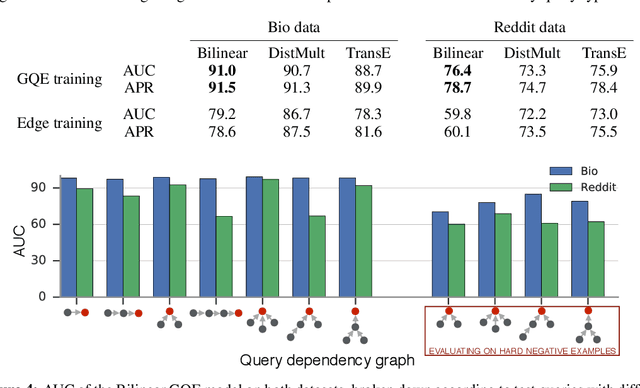
Learning low-dimensional embeddings of knowledge graphs is a powerful approach used to predict unobserved or missing edges between entities. However, an open challenge in this area is developing techniques that can go beyond simple edge prediction and handle more complex logical queries, which might involve multiple unobserved edges, entities, and variables. For instance, given an incomplete biological knowledge graph, we might want to predict "em what drugs are likely to target proteins involved with both diseases X and Y?" -- a query that requires reasoning about all possible proteins that {\em might} interact with diseases X and Y. Here we introduce a framework to efficiently make predictions about conjunctive logical queries -- a flexible but tractable subset of first-order logic -- on incomplete knowledge graphs. In our approach, we embed graph nodes in a low-dimensional space and represent logical operators as learned geometric operations (e.g., translation, rotation) in this embedding space. By performing logical operations within a low-dimensional embedding space, our approach achieves a time complexity that is linear in the number of query variables, compared to the exponential complexity required by a naive enumeration-based approach. We demonstrate the utility of this framework in two application studies on real-world datasets with millions of relations: predicting logical relationships in a network of drug-gene-disease interactions and in a graph-based representation of social interactions derived from a popular web forum.

Inferring Generative Model Structure with Static Analysis

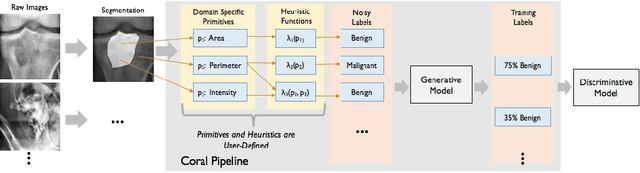
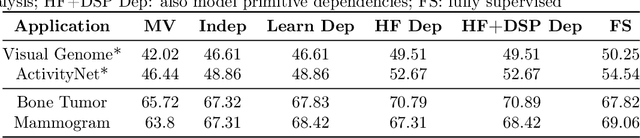
Obtaining enough labeled data to robustly train complex discriminative models is a major bottleneck in the machine learning pipeline. A popular solution is combining multiple sources of weak supervision using generative models. The structure of these models affects training label quality, but is difficult to learn without any ground truth labels. We instead rely on these weak supervision sources having some structure by virtue of being encoded programmatically. We present Coral, a paradigm that infers generative model structure by statically analyzing the code for these heuristics, thus reducing the data required to learn structure significantly. We prove that Coral's sample complexity scales quasilinearly with the number of heuristics and number of relations found, improving over the standard sample complexity, which is exponential in $n$ for identifying $n^{\textrm{th}}$ degree relations. Experimentally, Coral matches or outperforms traditional structure learning approaches by up to 3.81 F1 points. Using Coral to model dependencies instead of assuming independence results in better performance than a fully supervised model by 3.07 accuracy points when heuristics are used to label radiology data without ground truth labels.