Bottleneck potentials in Markov Random Fields

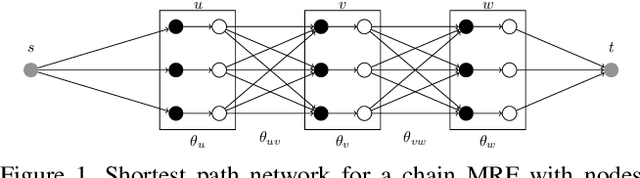
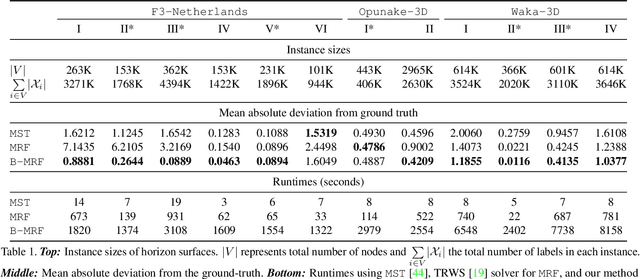
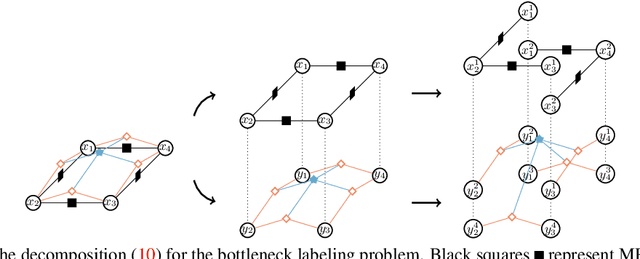
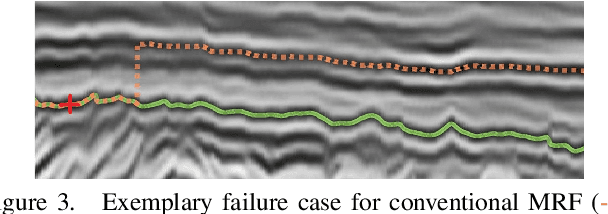
We consider general discrete Markov Random Fields(MRFs) with additional bottleneck potentials which penalize the maximum (instead of the sum) over local potential value taken by the MRF-assignment. Bottleneck potentials or analogous constructions have been considered in (i) combinatorial optimization (e.g. bottleneck shortest path problem, the minimum bottleneck spanning tree problem, bottleneck function minimization in greedoids), (ii) inverse problems with $L_{\infty}$-norm regularization, and (iii) valued constraint satisfaction on the $(\min,\max)$-pre-semirings. Bottleneck potentials for general discrete MRFs are a natural generalization of the above direction of modeling work to Maximum-A-Posteriori (MAP) inference in MRFs. To this end, we propose MRFs whose objective consists of two parts: terms that factorize according to (i) $(\min,+)$, i.e. potentials as in plain MRFs, and (ii) $(\min,\max)$, i.e. bottleneck potentials. To solve the ensuing inference problem, we propose high-quality relaxations and efficient algorithms for solving them. We empirically show efficacy of our approach on large scale seismic horizon tracking problems.

Higher-order Projected Power Iterations for Scalable Multi-Matching

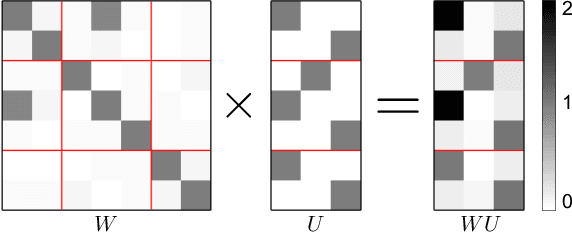
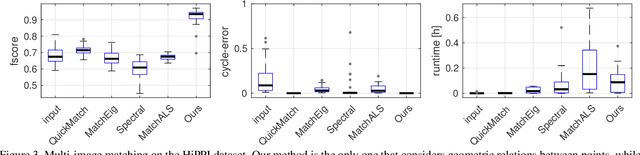
The matching of multiple objects (e.g. shapes or images) is a fundamental problem in vision and graphics. In order to robustly handle ambiguities, noise and repetitive patterns in challenging real-world settings, it is essential to take geometric consistency between points into account. Computationally, the multi-matching problem is difficult. It can be phrased as simultaneously solving multiple (NP-hard) quadratic assignment problems (QAPs) that are coupled via cycle-consistency constraints. The main limitations of existing multi-matching methods are that they either ignore geometric consistency and thus have limited robustness, or they are restricted to small-scale problems due to their (relatively) high computational cost. We address these shortcomings by introducing a Higher-order Projected Power Iteration method, which is (i) efficient and scales to tens of thousands of points, (ii) straightforward to implement, (iii) able to incorporate geometric consistency, and (iv) guarantees cycle-consistent multi-matchings. Experimentally we show that our approach is superior to existing methods.

MAP inference via Block-Coordinate Frank-Wolfe Algorithm

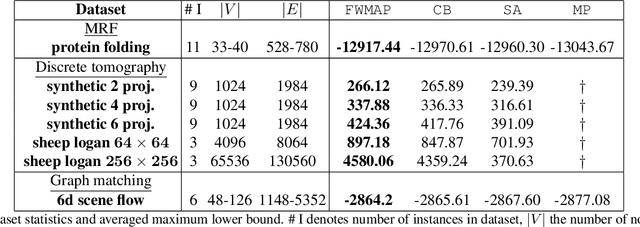
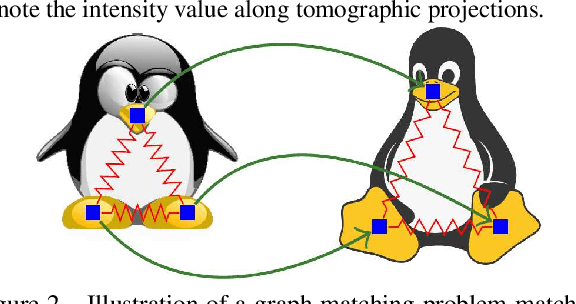
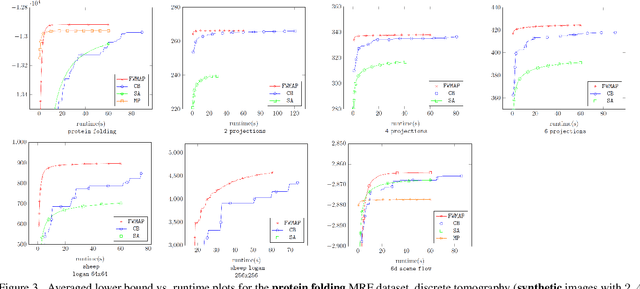
We present a new proximal bundle method for Maximum-A-Posteriori (MAP) inference in structured energy minimization problems. The method optimizes a Lagrangean relaxation of the original energy minimization problem using a multi plane block-coordinate Frank-Wolfe method that takes advantage of the specific structure of the Lagrangean decomposition. We show empirically that our method outperforms state-of-the-art Lagrangean decomposition based algorithms on some challenging Markov Random Field, multi-label discrete tomography and graph matching problems.

Maximum Persistency via Iterative Relaxed Inference with Graphical Models

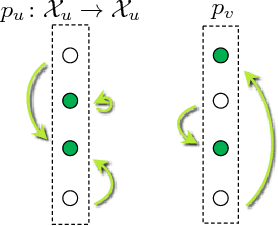
We consider the NP-hard problem of MAP-inference for undirected discrete graphical models. We propose a polynomial time and practically efficient algorithm for finding a part of its optimal solution. Specifically, our algorithm marks some labels of the considered graphical model either as (i) optimal, meaning that they belong to all optimal solutions of the inference problem; (ii) non-optimal if they provably do not belong to any solution. With access to an exact solver of a linear programming relaxation to the MAP-inference problem, our algorithm marks the maximal possible (in a specified sense) number of labels. We also present a version of the algorithm, which has access to a suboptimal dual solver only and still can ensure the (non-)optimality for the marked labels, although the overall number of the marked labels may decrease. We propose an efficient implementation, which runs in time comparable to a single run of a suboptimal dual solver. Our method is well-scalable and shows state-of-the-art results on computational benchmarks from machine learning and computer vision.

A Message Passing Algorithm for the Minimum Cost Multicut Problem

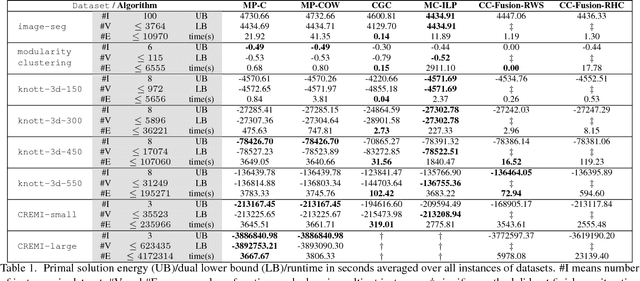
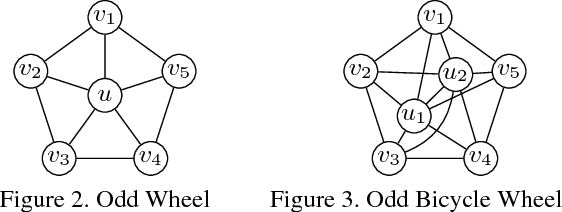
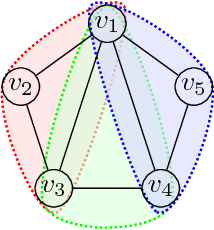
We propose a dual decomposition and linear program relaxation of the NP -hard minimum cost multicut problem. Unlike other polyhedral relaxations of the multicut polytope, it is amenable to efficient optimization by message passing. Like other polyhedral elaxations, it can be tightened efficiently by cutting planes. We define an algorithm that alternates between message passing and efficient separation of cycle- and odd-wheel inequalities. This algorithm is more efficient than state-of-the-art algorithms based on linear programming, including algorithms written in the framework of leading commercial software, as we show in experiments with large instances of the problem from applications in computer vision, biomedical image analysis and data mining.

A Dual Ascent Framework for Lagrangean Decomposition of Combinatorial Problems

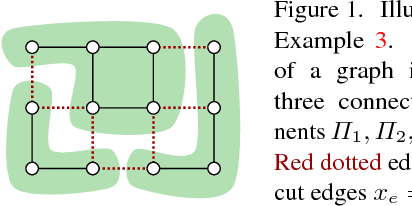
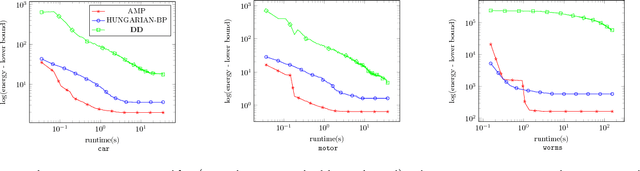
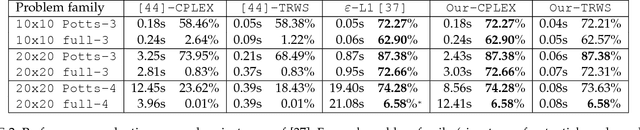
We propose a general dual ascent framework for Lagrangean decomposition of combinatorial problems. Although methods of this type have shown their efficiency for a number of problems, so far there was no general algorithm applicable to multiple problem types. In his work, we propose such a general algorithm. It depends on several parameters, which can be used to optimize its performance in each particular setting. We demonstrate efficacy of our method on graph matching and multicut problems, where it outperforms state-of-the-art solvers including those based on subgradient optimization and off-the-shelf linear programming solvers.

A Study of Lagrangean Decompositions and Dual Ascent Solvers for Graph Matching

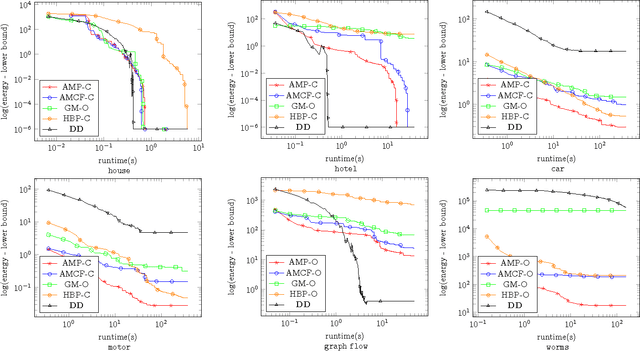
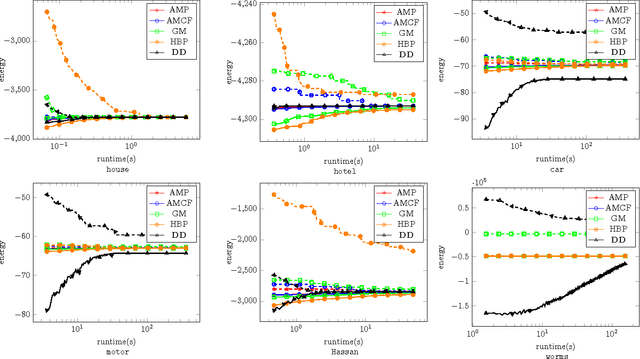
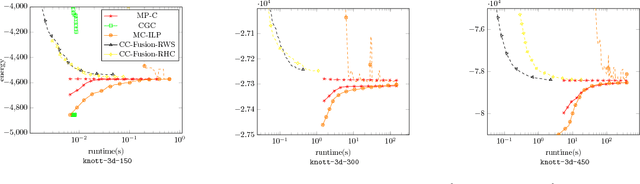
We study the quadratic assignment problem, in computer vision also known as graph matching. Two leading solvers for this problem optimize the Lagrange decomposition duals with sub-gradient and dual ascent (also known as message passing) updates. We explore s direction further and propose several additional Lagrangean relaxations of the graph matching problem along with corresponding algorithms, which are all based on a common dual ascent framework. Our extensive empirical evaluation gives several theoretical insights and suggests a new state-of-the-art any-time solver for the considered problem. Our improvement over state-of-the-art is particularly visible on a new dataset with large-scale sparse problem instances containing more than 500 graph nodes each.

Multicuts and Perturb & MAP for Probabilistic Graph Clustering

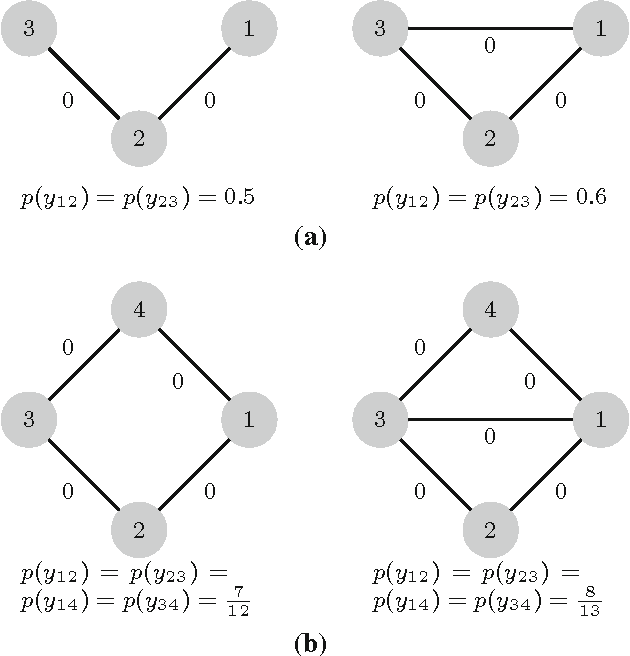
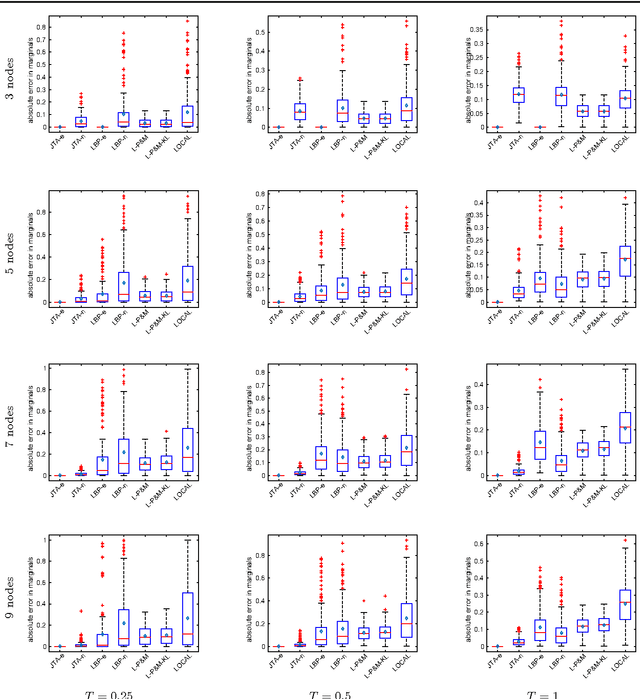
We present a probabilistic graphical model formulation for the graph clustering problem. This enables to locally represent uncertainty of image partitions by approximate marginal distributions in a mathematically substantiated way, and to rectify local data term cues so as to close contours and to obtain valid partitions. We exploit recent progress on globally optimal MAP inference by integer programming and on perturbation-based approximations of the log-partition function, in order to sample clusterings and to estimate marginal distributions of node-pairs both more accurately and more efficiently than state-of-the-art methods. Our approach works for any graphically represented problem instance. This is demonstrated for image segmentation and social network cluster analysis. Our mathematical ansatz should be relevant also for other combinatorial problems.

Partial Optimality by Pruning for MAP-Inference with General Graphical Models

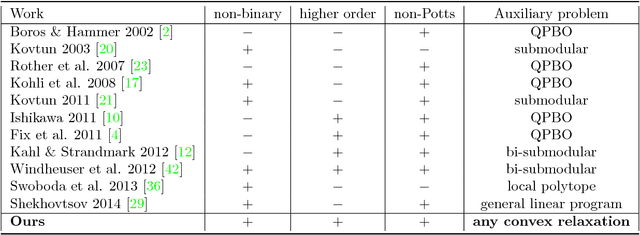
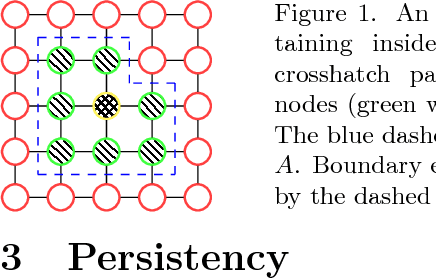
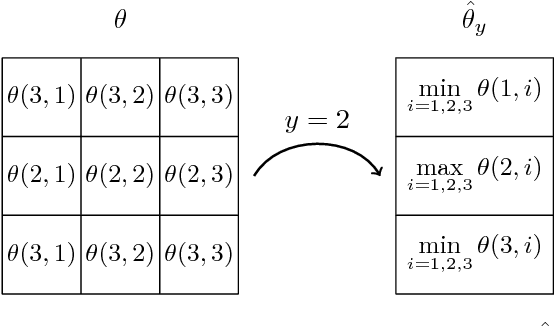
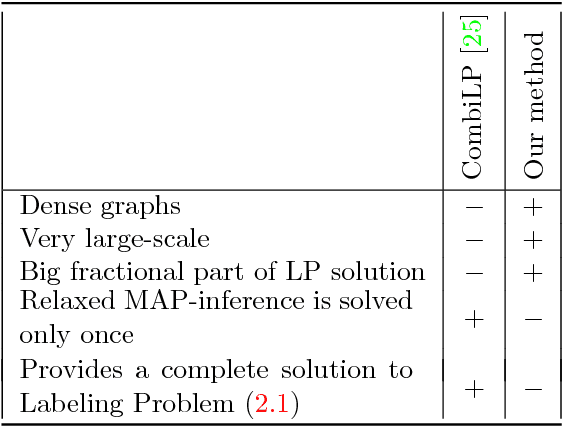
We consider the energy minimization problem for undirected graphical models, also known as MAP-inference problem for Markov random fields which is NP-hard in general. We propose a novel polynomial time algorithm to obtain a part of its optimal non-relaxed integral solution. Our algorithm is initialized with variables taking integral values in the solution of a convex relaxation of the MAP-inference problem and iteratively prunes those, which do not satisfy our criterion for partial optimality. We show that our pruning strategy is in a certain sense theoretically optimal. Also empirically our method outperforms previous approaches in terms of the number of persistently labelled variables. The method is very general, as it is applicable to models with arbitrary factors of an arbitrary order and can employ any solver for the considered relaxed problem. Our method's runtime is determined by the runtime of the convex relaxation solver for the MAP-inference problem.

Convex Variational Image Restoration with Histogram Priors

We present a novel variational approach to image restoration (e.g., denoising, inpainting, labeling) that enables to complement established variational approaches with a histogram-based prior enforcing closeness of the solution to some given empirical measure. By minimizing a single objective function, the approach utilizes simultaneously two quite different sources of information for restoration: spatial context in terms of some smoothness prior and non-spatial statistics in terms of the novel prior utilizing the Wasserstein distance between probability measures. We study the combination of the functional lifting technique with two different relaxations of the histogram prior and derive a jointly convex variational approach. Mathematical equivalence of both relaxations is established and cases where optimality holds are discussed. Additionally, we present an efficient algorithmic scheme for the numerical treatment of the presented model. Experiments using the basic total-variation based denoising approach as a case study demonstrate our novel regularization approach.