Nonlinear embeddings for conserving Hamiltonians and other quantities with Neural Galerkin schemes

This work focuses on the conservation of quantities such as Hamiltonians, mass, and momentum when solution fields of partial differential equations are approximated with nonlinear parametrizations such as deep networks. The proposed approach builds on Neural Galerkin schemes that are based on the Dirac--Frenkel variational principle to train nonlinear parametrizations sequentially in time. We first show that only adding constraints that aim to conserve quantities in continuous time can be insufficient because the nonlinear dependence on the parameters implies that even quantities that are linear in the solution fields become nonlinear in the parameters and thus are challenging to discretize in time. Instead, we propose Neural Galerkin schemes that compute at each time step an explicit embedding onto the manifold of nonlinearly parametrized solution fields to guarantee conservation of quantities. The embeddings can be combined with standard explicit and implicit time integration schemes. Numerical experiments demonstrate that the proposed approach conserves quantities up to machine precision.

Risk Assessment for Machine Learning Models

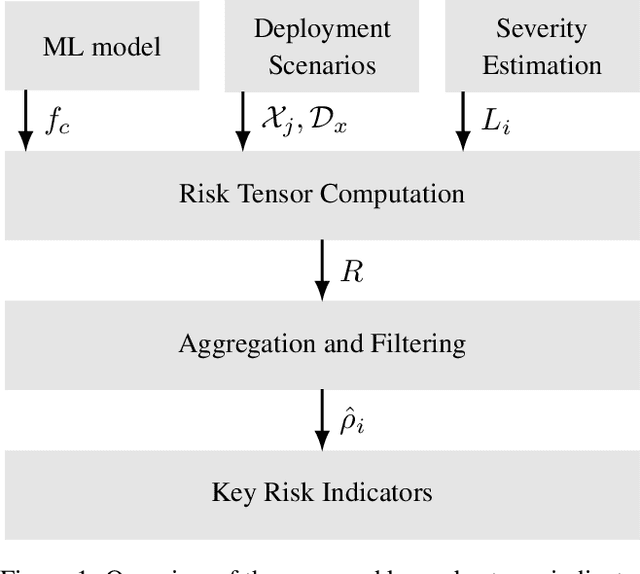
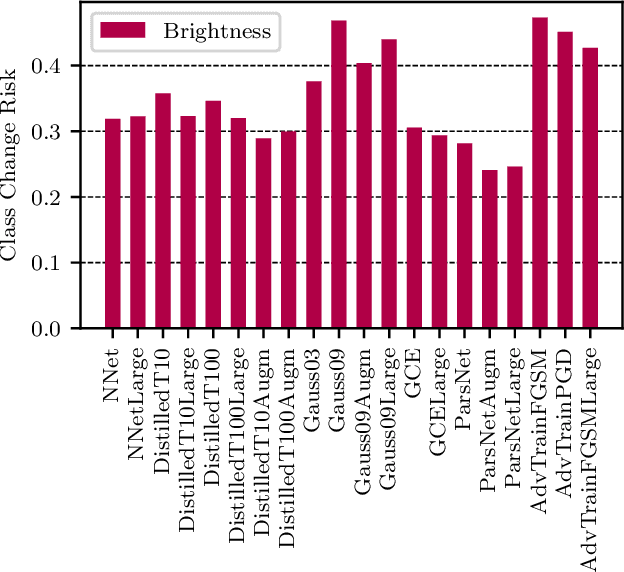
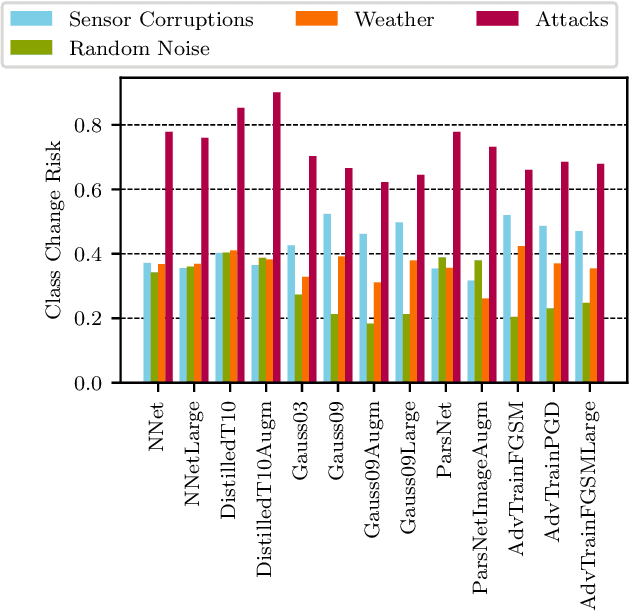
In this paper we propose a framework for assessing the risk associated with deploying a machine learning model in a specified environment. For that we carry over the risk definition from decision theory to machine learning. We develop and implement a method that allows to define deployment scenarios, test the machine learning model under the conditions specified in each scenario, and estimate the damage associated with the output of the machine learning model under test. Using the likelihood of each scenario together with the estimated damage we define \emph{key risk indicators} of a machine learning model. The definition of scenarios and weighting by their likelihood allows for standardized risk assessment in machine learning throughout multiple domains of application. In particular, in our framework, the robustness of a machine learning model to random input corruptions, distributional shifts caused by a changing environment, and adversarial perturbations can be assessed.