Parametric model reduction of mean-field and stochastic systems via higher-order action matching

The aim of this work is to learn models of population dynamics of physical systems that feature stochastic and mean-field effects and that depend on physics parameters. The learned models can act as surrogates of classical numerical models to efficiently predict the system behavior over the physics parameters. Building on the Benamou-Brenier formula from optimal transport and action matching, we use a variational problem to infer parameter- and time-dependent gradient fields that represent approximations of the population dynamics. The inferred gradient fields can then be used to rapidly generate sample trajectories that mimic the dynamics of the physical system on a population level over varying physics parameters. We show that combining Monte Carlo sampling with higher-order quadrature rules is critical for accurately estimating the training objective from sample data and for stabilizing the training process. We demonstrate on Vlasov-Poisson instabilities as well as on high-dimensional particle and chaotic systems that our approach accurately predicts population dynamics over a wide range of parameters and outperforms state-of-the-art diffusion-based and flow-based modeling that simply condition on time and physics parameters.

CoLoRA: Continuous low-rank adaptation for reduced implicit neural modeling of parameterized partial differential equations

This work introduces reduced models based on Continuous Low Rank Adaptation (CoLoRA) that pre-train neural networks for a given partial differential equation and then continuously adapt low-rank weights in time to rapidly predict the evolution of solution fields at new physics parameters and new initial conditions. The adaptation can be either purely data-driven or via an equation-driven variational approach that provides Galerkin-optimal approximations. Because CoLoRA approximates solution fields locally in time, the rank of the weights can be kept small, which means that only few training trajectories are required offline so that CoLoRA is well suited for data-scarce regimes. Predictions with CoLoRA are orders of magnitude faster than with classical methods and their accuracy and parameter efficiency is higher compared to other neural network approaches.

Neuronal Temporal Filters as Normal Mode Extractors

To generate actions in the face of physiological delays, the brain must predict the future. Here we explore how prediction may lie at the core of brain function by considering a neuron predicting the future of a scalar time series input. Assuming that the dynamics of the lag vector (a vector composed of several consecutive elements of the time series) are locally linear, Normal Mode Decomposition decomposes the dynamics into independently evolving (eigen-)modes allowing for straightforward prediction. We propose that a neuron learns the top mode and projects its input onto the associated subspace. Under this interpretation, the temporal filter of a neuron corresponds to the left eigenvector of a generalized eigenvalue problem. We mathematically analyze the operation of such an algorithm on noisy observations of synthetic data generated by a linear system. Interestingly, the shape of the temporal filter varies with the signal-to-noise ratio (SNR): a noisy input yields a monophasic filter and a growing SNR leads to multiphasic filters with progressively greater number of phases. Such variation in the temporal filter with input SNR resembles that observed experimentally in biological neurons.

Nonlinear embeddings for conserving Hamiltonians and other quantities with Neural Galerkin schemes

This work focuses on the conservation of quantities such as Hamiltonians, mass, and momentum when solution fields of partial differential equations are approximated with nonlinear parametrizations such as deep networks. The proposed approach builds on Neural Galerkin schemes that are based on the Dirac--Frenkel variational principle to train nonlinear parametrizations sequentially in time. We first show that only adding constraints that aim to conserve quantities in continuous time can be insufficient because the nonlinear dependence on the parameters implies that even quantities that are linear in the solution fields become nonlinear in the parameters and thus are challenging to discretize in time. Instead, we propose Neural Galerkin schemes that compute at each time step an explicit embedding onto the manifold of nonlinearly parametrized solution fields to guarantee conservation of quantities. The embeddings can be combined with standard explicit and implicit time integration schemes. Numerical experiments demonstrate that the proposed approach conserves quantities up to machine precision.

Randomized Sparse Neural Galerkin Schemes for Solving Evolution Equations with Deep Networks

Training neural networks sequentially in time to approximate solution fields of time-dependent partial differential equations can be beneficial for preserving causality and other physics properties; however, the sequential-in-time training is numerically challenging because training errors quickly accumulate and amplify over time. This work introduces Neural Galerkin schemes that update randomized sparse subsets of network parameters at each time step. The randomization avoids overfitting locally in time and so helps prevent the error from accumulating quickly over the sequential-in-time training, which is motivated by dropout that addresses a similar issue of overfitting due to neuron co-adaptation. The sparsity of the update reduces the computational costs of training without losing expressiveness because many of the network parameters are redundant locally at each time step. In numerical experiments with a wide range of evolution equations, the proposed scheme with randomized sparse updates is up to two orders of magnitude more accurate at a fixed computational budget and up to two orders of magnitude faster at a fixed accuracy than schemes with dense updates.

Representational dissimilarity metric spaces for stochastic neural networks

Quantifying similarity between neural representations -- e.g. hidden layer activation vectors -- is a perennial problem in deep learning and neuroscience research. Existing methods compare deterministic responses (e.g. artificial networks that lack stochastic layers) or averaged responses (e.g., trial-averaged firing rates in biological data). However, these measures of deterministic representational similarity ignore the scale and geometric structure of noise, both of which play important roles in neural computation. To rectify this, we generalize previously proposed shape metrics (Williams et al. 2021) to quantify differences in stochastic representations. These new distances satisfy the triangle inequality, and thus can be used as a rigorous basis for many supervised and unsupervised analyses. Leveraging this novel framework, we find that the stochastic geometries of neurobiological representations of oriented visual gratings and naturalistic scenes respectively resemble untrained and trained deep network representations. Further, we are able to more accurately predict certain network attributes (e.g. training hyperparameters) from its position in stochastic (versus deterministic) shape space.

Bridging the Gap: Point Clouds for Merging Neurons in Connectomics

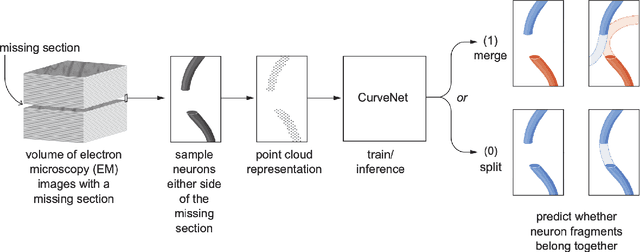
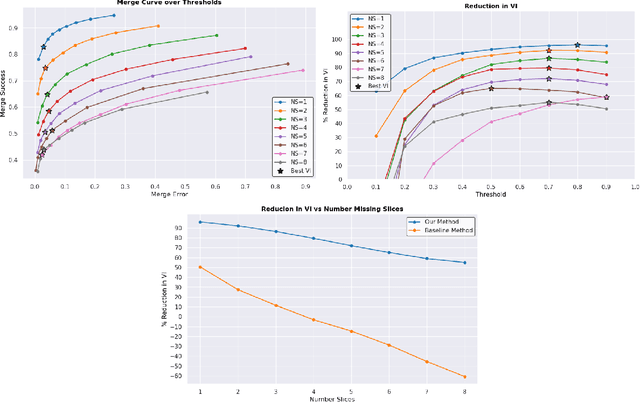
In the field of Connectomics, a primary problem is that of 3D neuron segmentation. Although deep learning-based methods have achieved remarkable accuracy, errors still exist, especially in regions with image defects. One common type of defect is that of consecutive missing image sections. Here, data is lost along some axis, and the resulting neuron segmentations are split across the gap. To address this problem, we propose a novel method based on point cloud representations of neurons. We formulate the problem as a classification problem and train CurveNet, a state-of-the-art point cloud classification model, to identify which neurons should be merged. We show that our method not only performs strongly but also scales reasonably to gaps well beyond what other methods have attempted to address. Additionally, our point cloud representations are highly efficient in terms of data, maintaining high performance with an amount of data that would be unfeasible for other methods. We believe that this is an indicator of the viability of using point cloud representations for other proofreading tasks.