Sparse POD Mode Selection and Manifold Dimensionality Reduction with Neural Networks

High-performance computing enables simulation of high-dimensional physical systems, but downstream analyses such as inverse problems and control remain computationally expensive, motivating model order reduction (MOR) to construct efficient low-dimensional surrogates. Proper Orthogonal Decomposition (POD), a widely adopted data-driven MOR method, projects dynamics onto linear subspaces spanned by the most energetic modes. However, POD struggles for problems with slowly decaying Kolmogorov \(n\)-widths, such as advection-dominated and turbulent flows, requiring many modes for accurate reconstruction. Moreover, energy-based selection can discard crucial low-energy modes needed to capture small-scale features. Recent nonlinear manifold methods using polynomial mappings with alternating or greedy mode selection achieve better reconstruction with fewer modes. However, these methods fix the nonlinear mapping form a priori, limiting expressivity. Conversely, neural network (NN) manifolds offer greater expressivity but employ energy-based selection. We present SparseModesNet, a dimensionality reduction framework that employs linear encoding via POD modes and nonlinear NN decoding. The decoder leverages LassoNet, a method enforcing hierarchical sparsity through residual connections with linear skip layers, to simultaneously select informative POD modes and learn a nonlinear mapping that minimizes reconstruction error. On benchmark advection-dominated and chaotic flows, SparseModesNet matches or exceeds state-of-the-art performance. For turbulent channel flow at friction Reynolds number \(Re_τ=5200\), we reduce reconstruction error by 51--78\% compared to existing polynomial manifold methods while maintaining interpretability through physically meaningful mode selection.

Streaming Operator Inference for Model Reduction of Large-Scale Dynamical Systems

Projection-based model reduction enables efficient simulation of complex dynamical systems by constructing low-dimensional surrogate models from high-dimensional data. The Operator Inference (OpInf) approach learns such reduced surrogate models through a two-step process: constructing a low-dimensional basis via Singular Value Decomposition (SVD) to compress the data, then solving a linear least-squares (LS) problem to infer reduced operators that govern the dynamics in this compressed space, all without access to the underlying code or full model operators, i.e., non-intrusively. Traditional OpInf operates as a batch learning method, where both the SVD and LS steps process all data simultaneously. This poses a barrier to deployment of the approach on large-scale applications where dataset sizes prevent the loading of all data into memory at once. Additionally, the traditional batch approach does not naturally allow model updates using new data acquired during online computation. To address these limitations, we propose Streaming OpInf, which learns reduced models from sequentially arriving data streams. Our approach employs incremental SVD for adaptive basis construction and recursive LS for streaming operator updates, eliminating the need to store complete data sets while enabling online model adaptation. The approach can flexibly combine different choices of streaming algorithms for numerical linear algebra: we systematically explore the impact of these choices both analytically and numerically to identify effective combinations for accurate reduced model learning. Numerical experiments on benchmark problems and a large-scale turbulent channel flow demonstrate that Streaming OpInf achieves accuracy comparable to batch OpInf while reducing memory requirements by over 99% and enabling dimension reductions exceeding 31,000x, resulting in orders-of-magnitude faster predictions.

Operator Inference Aware Quadratic Manifolds with Isotropic Reduced Coordinates for Nonintrusive Model Reduction

Quadratic manifolds for nonintrusive reduced modeling are typically trained to minimize the reconstruction error on snapshot data, which means that the error of models fitted to the embedded data in downstream learning steps is ignored. In contrast, we propose a greedy training procedure that takes into account both the reconstruction error on the snapshot data and the prediction error of reduced models fitted to the data. Because our procedure learns quadratic manifolds with the objective of achieving accurate reduced models, it avoids oscillatory and other non-smooth embeddings that can hinder learning accurate reduced models. Numerical experiments on transport and turbulent flow problems show that quadratic manifolds trained with the proposed greedy approach lead to reduced models with up to two orders of magnitude higher accuracy than quadratic manifolds trained with respect to the reconstruction error alone.

A block-random algorithm for learning on distributed, heterogeneous data

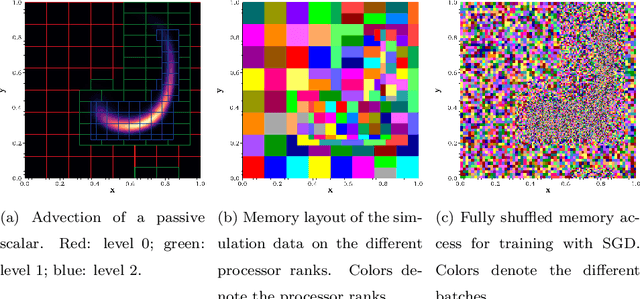
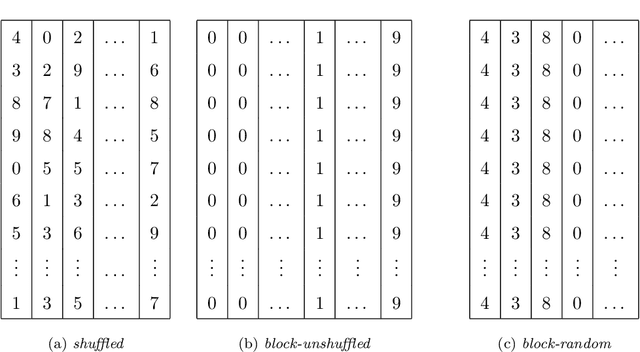
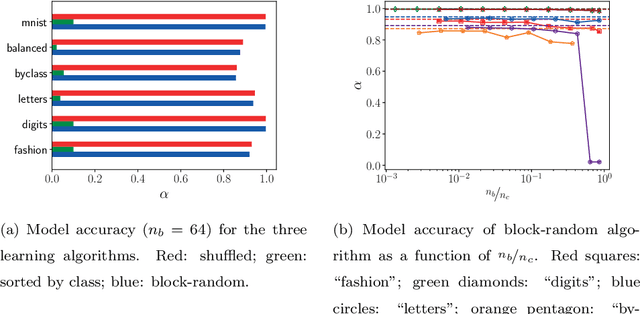
Most deep learning models are based on deep neural networks with multiple layers between input and output. The parameters defining these layers are initialized using random values and are "learned" from data, typically using stochastic gradient descent based algorithms. These algorithms rely on data being randomly shuffled before optimization. The randomization of the data prior to processing in batches that is formally required for stochastic gradient descent algorithm to effectively derive a useful deep learning model is expected to be prohibitively expensive for in situ model training because of the resulting data communications across the processor nodes. We show that the stochastic gradient descent (SGD) algorithm can still make useful progress if the batches are defined on a per-processor basis and processed in random order even though (i) the batches are constructed from data samples from a single class or specific flow region, and (ii) the overall data samples are heterogeneous. We present block-random gradient descent, a new algorithm that works on distributed, heterogeneous data without having to pre-shuffle. This algorithm enables in situ learning for exascale simulations. The performance of this algorithm is demonstrated on a set of benchmark classification models and the construction of a subgrid scale large eddy simulations (LES) model for turbulent channel flow using a data model similar to that which will be encountered in exascale simulation.