Global Guarantees for Blind Demodulation with Generative Priors

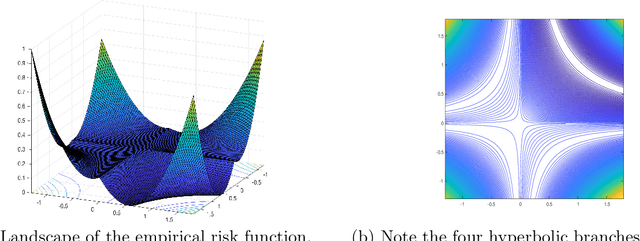
We study a deep learning inspired formulation for the blind demodulation problem, which is the task of recovering two unknown vectors from their entrywise multiplication. We consider the case where the unknown vectors are in the range of known deep generative models, $\mathcal{G}^{(1)}:\mathbb{R}^n\rightarrow\mathbb{R}^\ell$ and $\mathcal{G}^{(2)}:\mathbb{R}^p\rightarrow\mathbb{R}^\ell$. In the case when the networks corresponding to the generative models are expansive, the weight matrices are random and the dimension of the unknown vectors satisfy $\ell = \Omega(n^2+p^2)$, up to log factors, we show that the empirical risk objective has a favorable landscape for optimization. That is, the objective function has a descent direction at every point outside of a small neighborhood around four hyperbolic curves. We also characterize the local maximizers of the empirical risk objective and, hence, show that there does not exist any other stationary points outside of these neighborhood around four hyperbolic curves and the set of local maximizers. We also implement a gradient descent scheme inspired by the geometry of the landscape of the objective function. In order to converge to a global minimizer, this gradient descent scheme exploits the fact that exactly one of the hyperbolic curve corresponds to the global minimizer, and thus points near this hyperbolic curve have a lower objective value than points close to the other spurious hyperbolic curves. We show that this gradient descent scheme can effectively remove distortions synthetically introduced to the MNIST dataset.

Invertible generative models for inverse problems: mitigating representation error and dataset bias

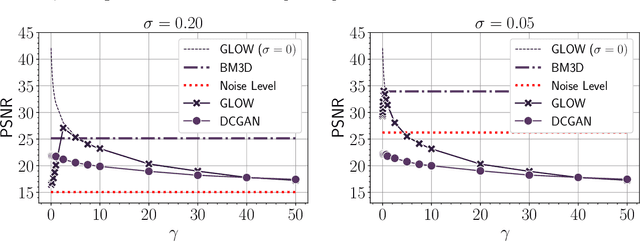
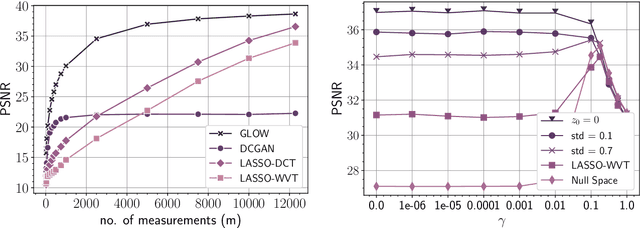
Trained generative models have shown remarkable performance as priors for inverse problems in imaging. For example, Generative Adversarial Network priors permit recovery of test images from 5-10x fewer measurements than sparsity priors. Unfortunately, these models may be unable to represent any particular image because of architectural choices, mode collapse, and bias in the training dataset. In this paper, we demonstrate that invertible neural networks, which have zero representation error by design, can be effective natural signal priors at inverse problems such as denoising, compressive sensing, and inpainting. Given a trained generative model, we study the empirical risk formulation of the desired inverse problem under a regularization that promotes high likelihood images, either directly by penalization or algorithmically by initialization. For compressive sensing, invertible priors can yield higher accuracy than sparsity priors across almost all undersampling ratios. For the same accuracy on test images, they can use 10-20x fewer measurements. We demonstrate that invertible priors can yield better reconstructions than sparsity priors for images that have rare features of variation within the biased training set, including out-of-distribution natural images.

Deep Decoder: Concise Image Representations from Untrained Non-convolutional Networks

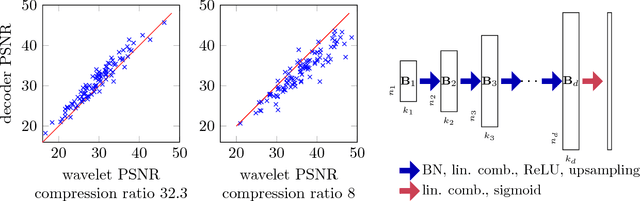
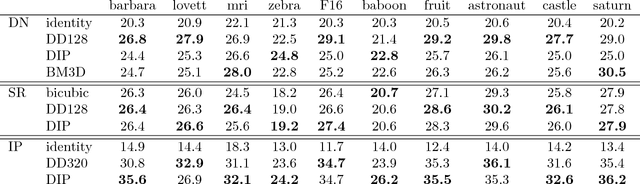
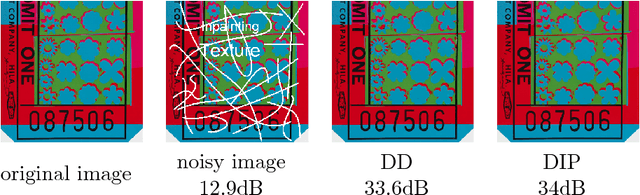
Deep neural networks, in particular convolutional neural networks, have become highly effective tools for compressing images and solving inverse problems including denoising, inpainting, and reconstruction from few and noisy measurements. This success can be attributed in part to their ability to represent and generate natural images well. Contrary to classical tools such as wavelets, image-generating deep neural networks have a large number of parameters---typically a multiple of their output dimension---and need to be trained on large datasets. In this paper, we propose an untrained simple image model, called the deep decoder, which is a deep neural network that can generate natural images from very few weight parameters. The deep decoder has a simple architecture with no convolutions and fewer weight parameters than the output dimensionality. This underparameterization enables the deep decoder to compress images into a concise set of network weights, which we show is on par with wavelet-based thresholding. Further, underparameterization provides a barrier to overfitting, allowing the deep decoder to have state-of-the-art performance for denoising. The deep decoder is simple in the sense that each layer has an identical structure that consists of only one upsampling unit, pixel-wise linear combination of channels, ReLU activation, and channelwise normalization. This simplicity makes the network amenable to theoretical analysis, and it sheds light on the aspects of neural networks that enable them to form effective signal representations.

Phase Retrieval Under a Generative Prior

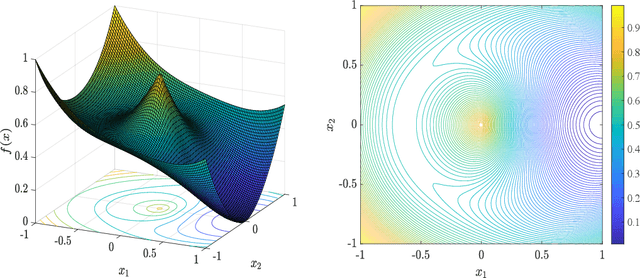
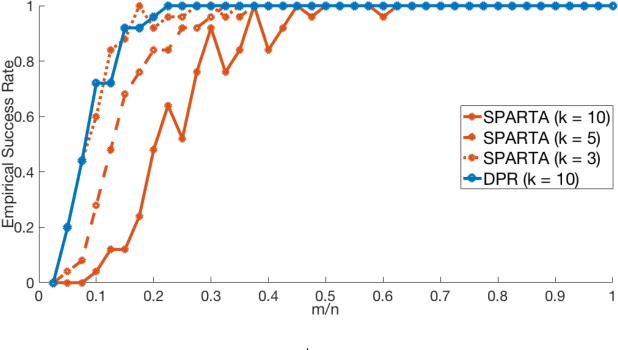
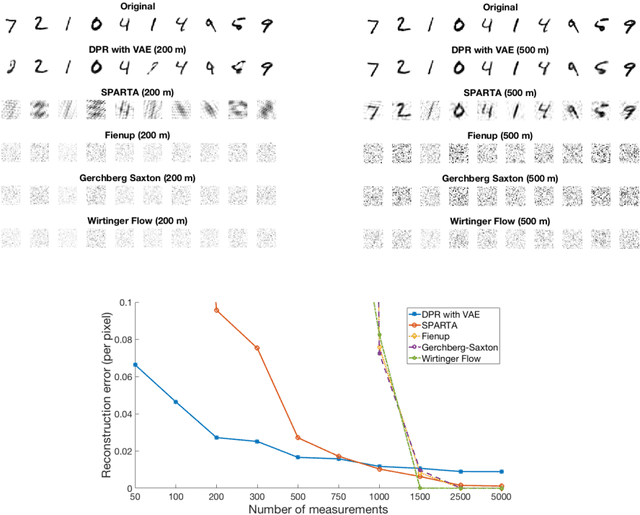
The phase retrieval problem asks to recover a natural signal $y_0 \in \mathbb{R}^n$ from $m$ quadratic observations, where $m$ is to be minimized. As is common in many imaging problems, natural signals are considered sparse with respect to a known basis, and the generic sparsity prior is enforced via $\ell_1$ regularization. While successful in the realm of linear inverse problems, such $\ell_1$ methods have encountered possibly fundamental limitations, as no computationally efficient algorithm for phase retrieval of a $k$-sparse signal has been proven to succeed with fewer than $O(k^2\log n)$ generic measurements, exceeding the theoretical optimum of $O(k \log n)$. In this paper, we propose a novel framework for phase retrieval by 1) modeling natural signals as being in the range of a deep generative neural network $G : \mathbb{R}^k \rightarrow \mathbb{R}^n$ and 2) enforcing this prior directly by optimizing an empirical risk objective over the domain of the generator. Our formulation has provably favorable global geometry for gradient methods, as soon as $m = O(kd^2\log n)$, where $d$ is the depth of the network. Specifically, when suitable deterministic conditions on the generator and measurement matrix are met, we construct a descent direction for any point outside of a small neighborhood around the unique global minimizer and its negative multiple, and show that such conditions hold with high probability under Gaussian ensembles of multilayer fully-connected generator networks and measurement matrices. This formulation for structured phase retrieval thus has two advantages over sparsity based methods: 1) deep generative priors can more tightly represent natural signals and 2) information theoretically optimal sample complexity. We corroborate these results with experiments showing that exploiting generative models in phase retrieval tasks outperforms sparse phase retrieval methods.

Deep Denoising: Rate-Optimal Recovery of Structured Signals with a Deep Prior

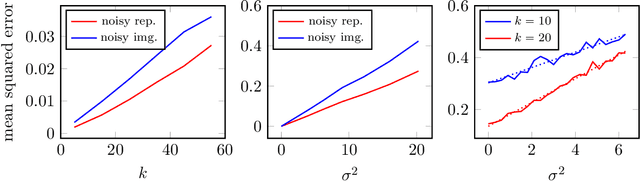
Deep neural networks provide state-of-the-art performance for image denoising, where the goal is to map a noisy image to a near noise-free image. The underlying principle is simple: images are well described by priors that map a low-dimensional latent representations to image. Based on a prior, a noisy image can be denoised by finding a close image in the range of the prior. Since deep networks trained on large set of images have empirically been shown to be good priors, they enable effective denoisers. However, there is little theory to justify this success, let alone to predict the denoising performance. In this paper we consider the problem of denoising an image from additive Gaussian noise with variance $\sigma^2$, assuming the image is well described by a deep neural network with ReLu activations functions, mapping a $k$-dimensional latent space to an $n$-dimensional image. We provide an iterative algorithm minimizing a non-convex loss that provably removes noise energy by a fraction $\sigma^2 k/n$. We also demonstrate in numerical experiments that this denoising performance is, indeed, achieved by generative priors learned from data.

Global Guarantees for Enforcing Deep Generative Priors by Empirical Risk

We examine the theoretical properties of enforcing priors provided by generative deep neural networks via empirical risk minimization. In particular we consider two models, one in which the task is to invert a generative neural network given access to its last layer and another in which the task is to invert a generative neural network given only compressive linear observations of its last layer. We establish that in both cases, in suitable regimes of network layer sizes and a randomness assumption on the network weights, that the non-convex objective function given by empirical risk minimization does not have any spurious stationary points. That is, we establish that with high probability, at any point away from small neighborhoods around two scalar multiples of the desired solution, there is a descent direction. Hence, there are no local minima, saddle points, or other stationary points outside these neighborhoods. These results constitute the first theoretical guarantees which establish the favorable global geometry of these non-convex optimization problems, and they bridge the gap between the empirical success of enforcing deep generative priors and a rigorous understanding of non-linear inverse problems.

A Convex Program for Mixed Linear Regression with a Recovery Guarantee for Well-Separated Data

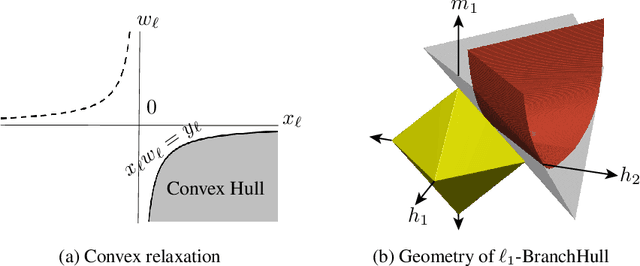
We introduce a convex approach for mixed linear regression over $d$ features. This approach is a second-order cone program, based on L1 minimization, which assigns an estimate regression coefficient in $\mathbb{R}^{d}$ for each data point. These estimates can then be clustered using, for example, $k$-means. For problems with two or more mixture classes, we prove that the convex program exactly recovers all of the mixture components in the noiseless setting under technical conditions that include a well-separation assumption on the data. Under these assumptions, recovery is possible if each class has at least $d$ independent measurements. We also explore an iteratively reweighted least squares implementation of this method on real and synthetic data.

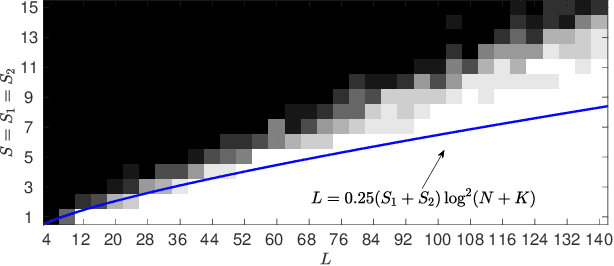
ShapeFit and ShapeKick for Robust, Scalable Structure from Motion

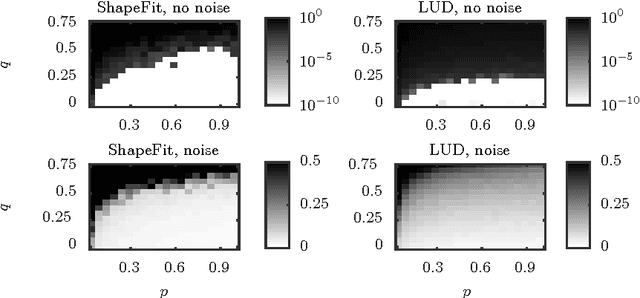
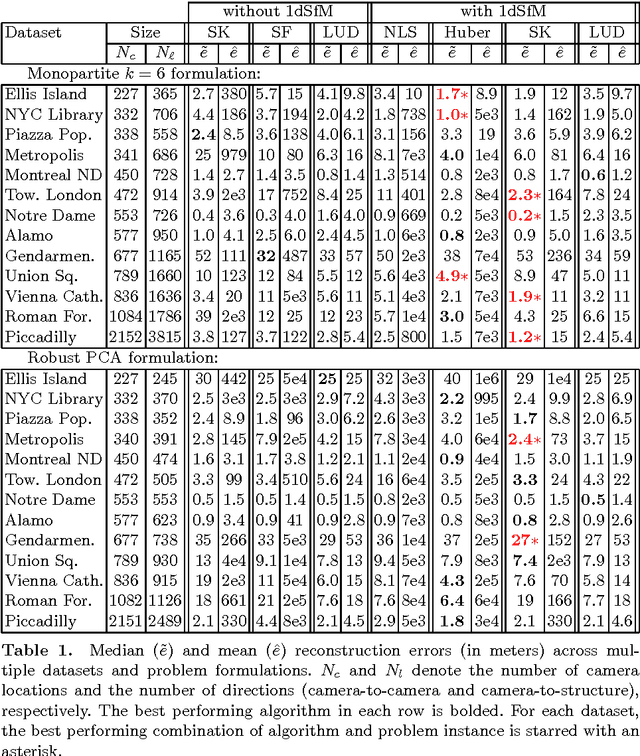
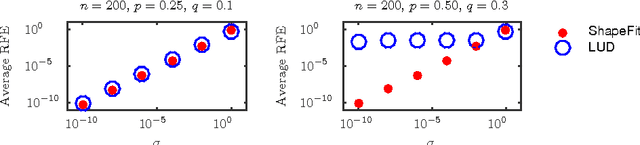
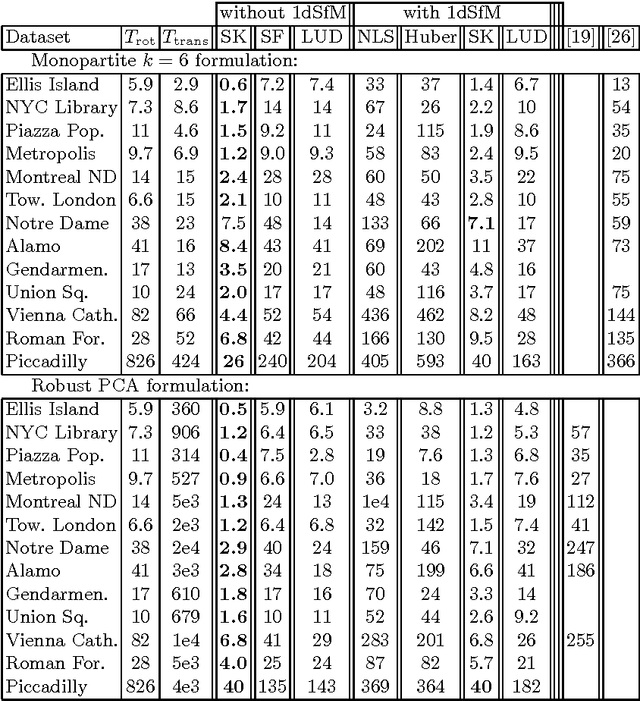
We introduce a new method for location recovery from pair-wise directions that leverages an efficient convex program that comes with exact recovery guarantees, even in the presence of adversarial outliers. When pairwise directions represent scaled relative positions between pairs of views (estimated for instance with epipolar geometry) our method can be used for location recovery, that is the determination of relative pose up to a single unknown scale. For this task, our method yields performance comparable to the state-of-the-art with an order of magnitude speed-up. Our proposed numerical framework is flexible in that it accommodates other approaches to location recovery and can be used to speed up other methods. These properties are demonstrated by extensively testing against state-of-the-art methods for location recovery on 13 large, irregular collections of images of real scenes in addition to simulated data with ground truth.

Exact simultaneous recovery of locations and structure from known orientations and corrupted point correspondences

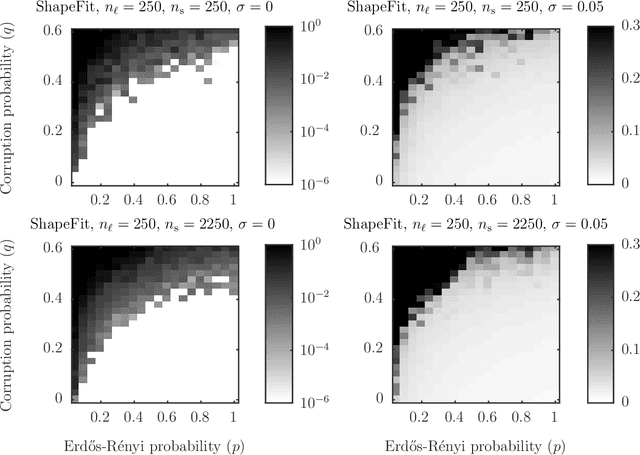
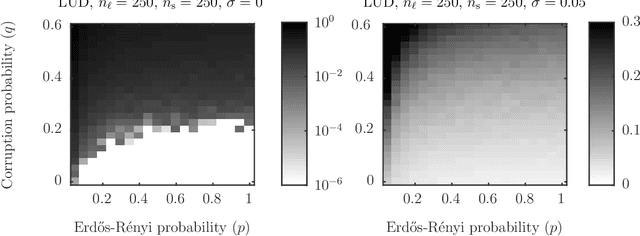
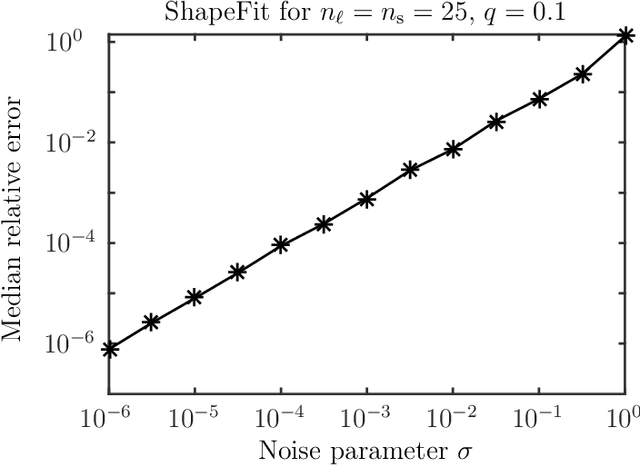
Let $t_1,\ldots,t_{n_l} \in \mathbb{R}^d$ and $p_1,\ldots,p_{n_s} \in \mathbb{R}^d$ and consider the bipartite location recovery problem: given a subset of pairwise direction observations $\{(t_i - p_j) / \|t_i - p_j\|_2\}_{i,j \in [n_l] \times [n_s]}$, where a constant fraction of these observations are arbitrarily corrupted, find $\{t_i\}_{i \in [n_ll]}$ and $\{p_j\}_{j \in [n_s]}$ up to a global translation and scale. We study the recently introduced ShapeFit algorithm as a method for solving this bipartite location recovery problem. In this case, ShapeFit consists of a simple convex program over $d(n_l + n_s)$ real variables. We prove that this program recovers a set of $n_l+n_s$ i.i.d. Gaussian locations exactly and with high probability if the observations are given by a bipartite Erd\H{o}s-R\'{e}nyi graph, $d$ is large enough, and provided that at most a constant fraction of observations involving any particular location are adversarially corrupted. This recovery theorem is based on a set of deterministic conditions that we prove are sufficient for exact recovery. Finally, we propose a modified pipeline for the Structure for Motion problem, based on this bipartite location recovery problem.

ShapeFit: Exact location recovery from corrupted pairwise directions

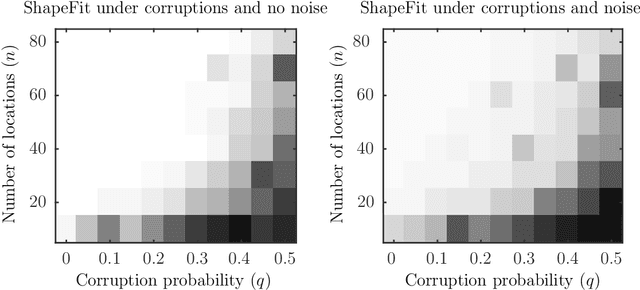
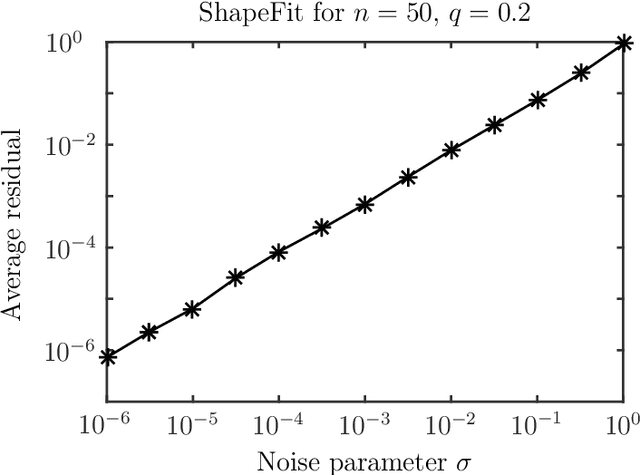
Let $t_1,\ldots,t_n \in \mathbb{R}^d$ and consider the location recovery problem: given a subset of pairwise direction observations $\{(t_i - t_j) / \|t_i - t_j\|_2\}_{i<j \in [n] \times [n]}$, where a constant fraction of these observations are arbitrarily corrupted, find $\{t_i\}_{i=1}^n$ up to a global translation and scale. We propose a novel algorithm for the location recovery problem, which consists of a simple convex program over $dn$ real variables. We prove that this program recovers a set of $n$ i.i.d. Gaussian locations exactly and with high probability if the observations are given by an \erdosrenyi graph, $d$ is large enough, and provided that at most a constant fraction of observations involving any particular location are adversarially corrupted. We also prove that the program exactly recovers Gaussian locations for $d=3$ if the fraction of corrupted observations at each location is, up to poly-logarithmic factors, at most a constant. Both of these recovery theorems are based on a set of deterministic conditions that we prove are sufficient for exact recovery.