Unmixing urban hyperspectral imagery with a Gaussian mixture model on endmember variability

In this paper, we model a pixel as a linear combination of endmembers sampled from probability distributions of Gaussian mixture models (GMM). The parameters of the GMM distributions are estimated using spectral libraries. Abundances are estimated based on the distribution parameters. The advantage of this algorithm is that the model size grows very slowly as a function of the library size. To validate this method, we used data collected by the AVIRIS sensor over the Santa Barbara region: two 16 m spatial resolution and two 4 m spatial resolution images. 64 validated regions of interest (ROI) (180 m by 180 m) were used to assess estimate accuracy. Ground truth was obtained using 1 m images leading to the following 6 classes: turfgrass, non-photosynthetic vegetation (NPV), paved, roof, soil, and tree. Spectral libraries were built by manually identifying and extracting pure spectra from both resolution images, resulting in 3,287 spectra at 16 m and 15,426 spectra at 4 m. We then unmixed ROIs of each resolution using the following unmixing algorithms: the set-based algorithms MESMA and AAM, and the distribution-based algorithms GMM, NCM, and BCM. The original libraries were used for the distribution-based algorithms whereas set-based methods required a sophisticated reduction method, resulting in reduced libraries of 61 spectra at 16 m and 95 spectra at 4 m. The results show that GMM performs best among the distribution-based methods, producing comparable accuracy to MESMA, and may be more robust across datasets.

A Gaussian mixture model representation of endmember variability in hyperspectral unmixing

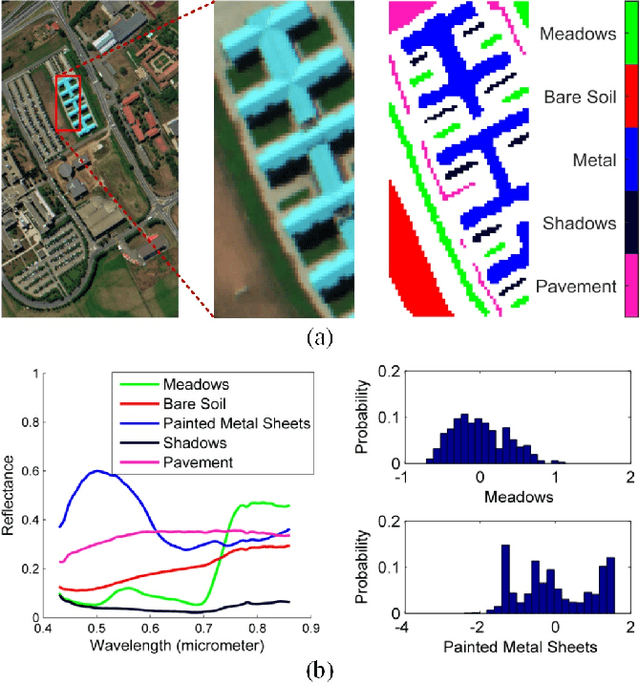
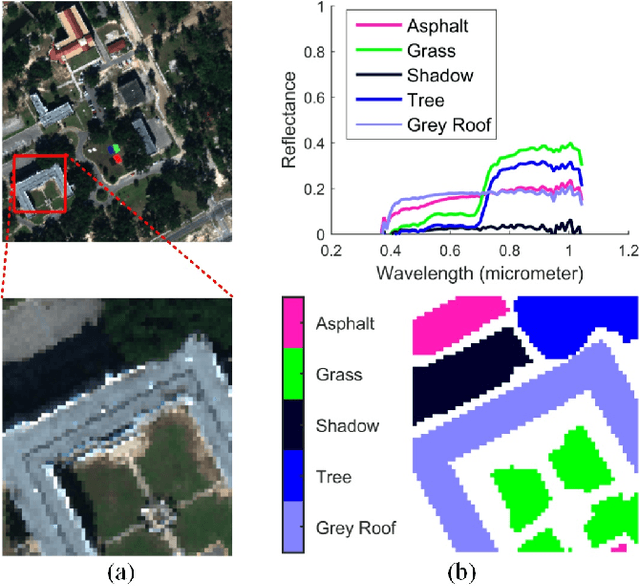
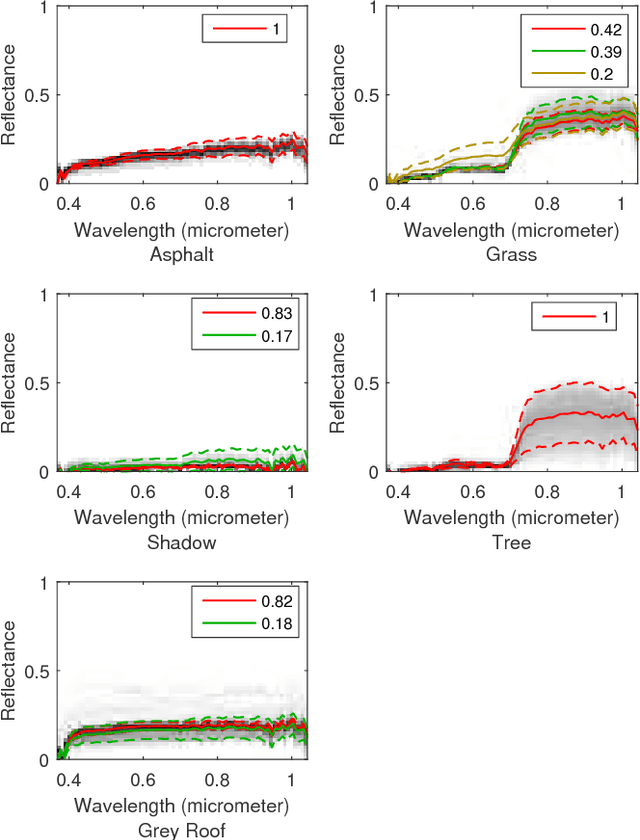
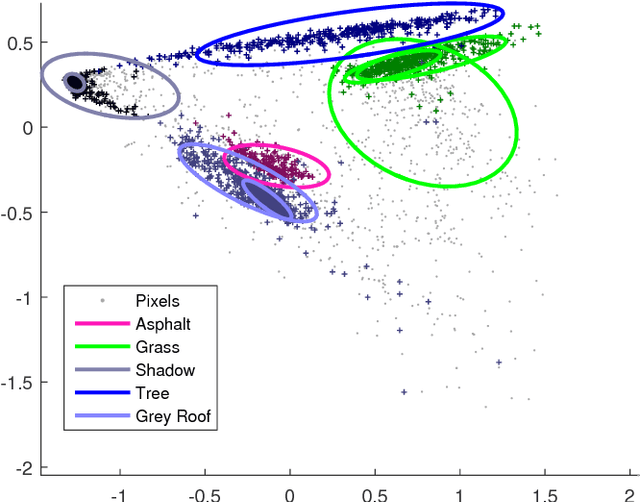
Hyperspectral unmixing while considering endmember variability is usually performed by the normal compositional model (NCM), where the endmembers for each pixel are assumed to be sampled from unimodal Gaussian distributions. However, in real applications, the distribution of a material is often not Gaussian. In this paper, we use Gaussian mixture models (GMM) to represent the endmember variability. We show, given the GMM starting premise, that the distribution of the mixed pixel (under the linear mixing model) is also a GMM (and this is shown from two perspectives). The first perspective originates from the random variable transformation and gives a conditional density function of the pixels given the abundances and GMM parameters. With proper smoothness and sparsity prior constraints on the abundances, the conditional density function leads to a standard maximum a posteriori (MAP) problem which can be solved using generalized expectation maximization. The second perspective originates from marginalizing over the endmembers in the GMM, which provides us with a foundation to solve for the endmembers at each pixel. Hence, our model can not only estimate the abundances and distribution parameters, but also the distinct endmember set for each pixel. We tested the proposed GMM on several synthetic and real datasets, and showed its potential by comparing it to current popular methods.