Patroklos Stefanou
Efficient Truncated Linear Regression with Unknown Noise Variance
Aug 25, 2022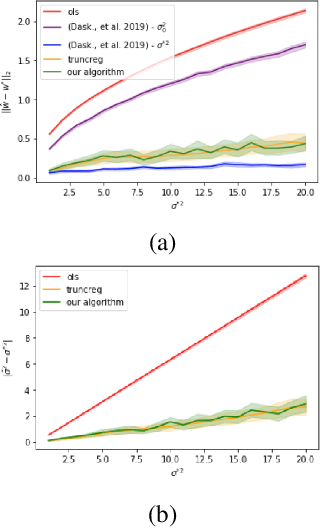
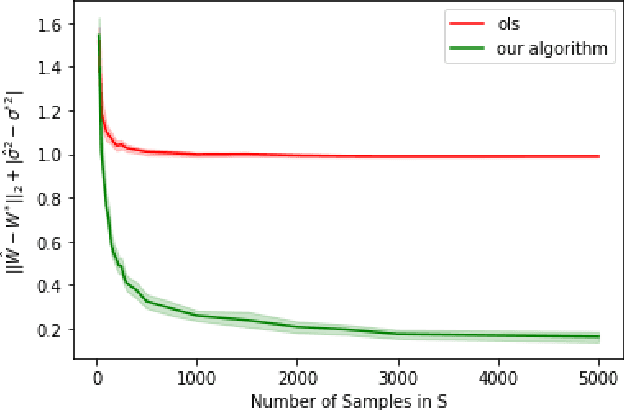
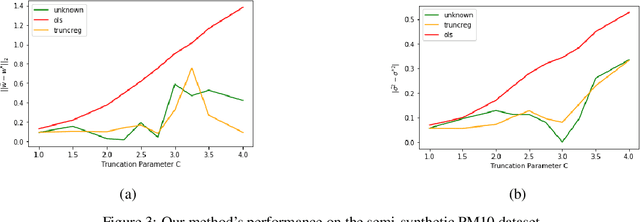
Abstract:Truncated linear regression is a classical challenge in Statistics, wherein a label, $y = w^T x + \varepsilon$, and its corresponding feature vector, $x \in \mathbb{R}^k$, are only observed if the label falls in some subset $S \subseteq \mathbb{R}$; otherwise the existence of the pair $(x, y)$ is hidden from observation. Linear regression with truncated observations has remained a challenge, in its general form, since the early works of~\citet{tobin1958estimation,amemiya1973regression}. When the distribution of the error is normal with known variance, recent work of~\citet{daskalakis2019truncatedregression} provides computationally and statistically efficient estimators of the linear model, $w$. In this paper, we provide the first computationally and statistically efficient estimators for truncated linear regression when the noise variance is unknown, estimating both the linear model and the variance of the noise. Our estimator is based on an efficient implementation of Projected Stochastic Gradient Descent on the negative log-likelihood of the truncated sample. Importantly, we show that the error of our estimates is asymptotically normal, and we use this to provide explicit confidence regions for our estimates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge