Paris Perdikaris
Fast PDE-constrained optimization via self-supervised operator learning
Oct 25, 2021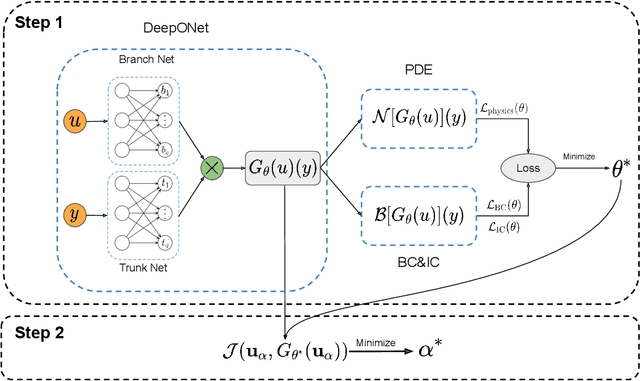

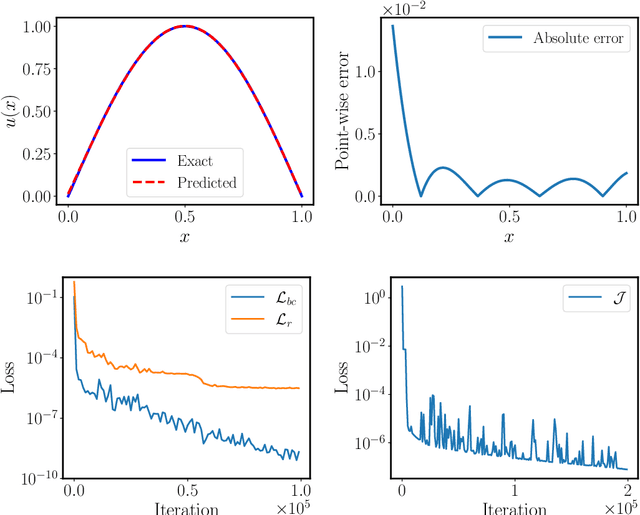
Abstract:Design and optimal control problems are among the fundamental, ubiquitous tasks we face in science and engineering. In both cases, we aim to represent and optimize an unknown (black-box) function that associates a performance/outcome to a set of controllable variables through an experiment. In cases where the experimental dynamics can be described by partial differential equations (PDEs), such problems can be mathematically translated into PDE-constrained optimization tasks, which quickly become intractable as the number of control variables and the cost of experiments increases. In this work we leverage physics-informed deep operator networks (DeepONets) -- a self-supervised framework for learning the solution operator of parametric PDEs -- to build fast and differentiable surrogates for rapidly solving PDE-constrained optimization problems, even in the absence of any paired input-output training data. The effectiveness of the proposed framework will be demonstrated across different applications involving continuous functions as control or design variables, including time-dependent optimal control of heat transfer, and drag minimization of obstacles in Stokes flow. In all cases, we observe that DeepONets can minimize high-dimensional cost functionals in a matter of seconds, yielding a significant speed up compared to traditional adjoint PDE solvers that are typically costly and limited to relatively low-dimensional control/design parametrizations.
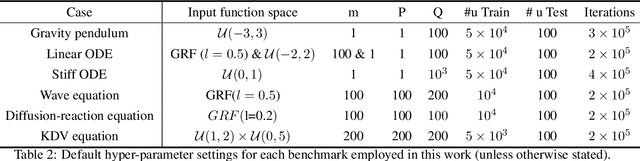
Improved architectures and training algorithms for deep operator networks
Oct 11, 2021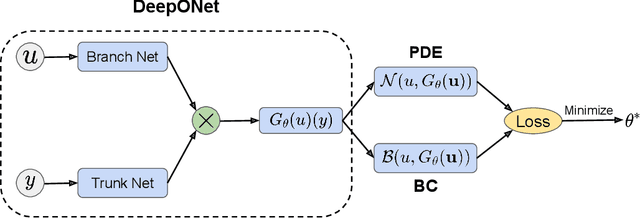

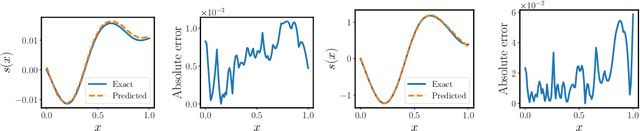

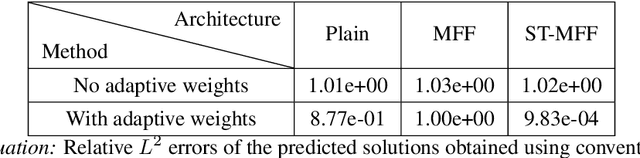
Abstract:Operator learning techniques have recently emerged as a powerful tool for learning maps between infinite-dimensional Banach spaces. Trained under appropriate constraints, they can also be effective in learning the solution operator of partial differential equations (PDEs) in an entirely self-supervised manner. In this work we analyze the training dynamics of deep operator networks (DeepONets) through the lens of Neural Tangent Kernel (NTK) theory, and reveal a bias that favors the approximation of functions with larger magnitudes. To correct this bias we propose to adaptively re-weight the importance of each training example, and demonstrate how this procedure can effectively balance the magnitude of back-propagated gradients during training via gradient descent. We also propose a novel network architecture that is more resilient to vanishing gradient pathologies. Taken together, our developments provide new insights into the training of DeepONets and consistently improve their predictive accuracy by a factor of 10-50x, demonstrated in the challenging setting of learning PDE solution operators in the absence of paired input-output observations. All code and data accompanying this manuscript are publicly available at \url{https://github.com/PredictiveIntelligenceLab/ImprovedDeepONets.}
Long-time integration of parametric evolution equations with physics-informed DeepONets
Jun 09, 2021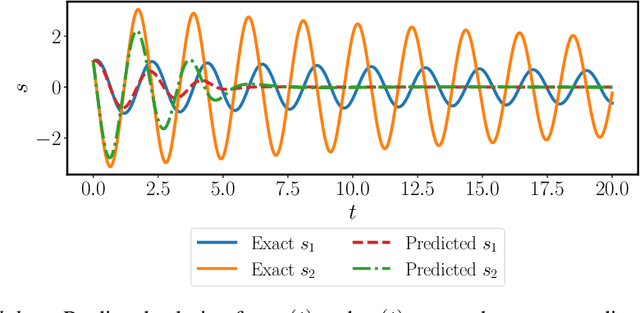
Abstract:Ordinary and partial differential equations (ODEs/PDEs) play a paramount role in analyzing and simulating complex dynamic processes across all corners of science and engineering. In recent years machine learning tools are aspiring to introduce new effective ways of simulating PDEs, however existing approaches are not able to reliably return stable and accurate predictions across long temporal horizons. We aim to address this challenge by introducing an effective framework for learning infinite-dimensional operators that map random initial conditions to associated PDE solutions within a short time interval. Such latent operators can be parametrized by deep neural networks that are trained in an entirely self-supervised manner without requiring any paired input-output observations. Global long-time predictions across a range of initial conditions can be then obtained by iteratively evaluating the trained model using each prediction as the initial condition for the next evaluation step. This introduces a new approach to temporal domain decomposition that is shown to be effective in performing accurate long-time simulations for a wide range of parametric ODE and PDE systems, from wave propagation, to reaction-diffusion dynamics and stiff chemical kinetics, all at a fraction of the computational cost needed by classical numerical solvers.
Learning the solution operator of parametric partial differential equations with physics-informed DeepOnets
Mar 19, 2021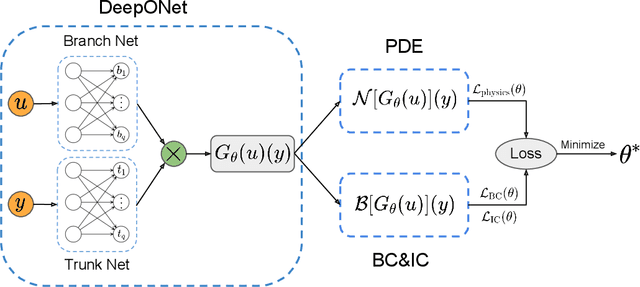

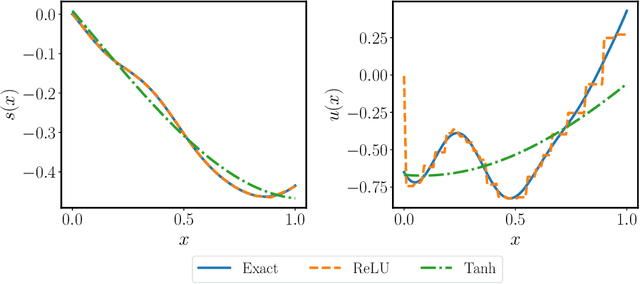

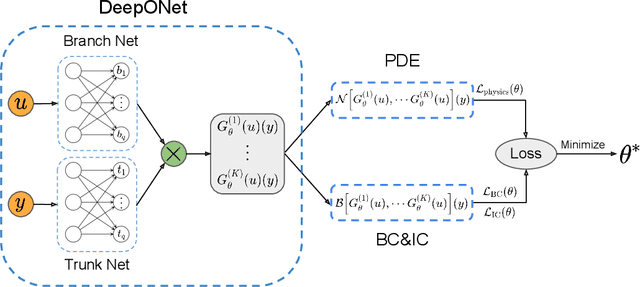
Abstract:Deep operator networks (DeepONets) are receiving increased attention thanks to their demonstrated capability to approximate nonlinear operators between infinite-dimensional Banach spaces. However, despite their remarkable early promise, they typically require large training data-sets consisting of paired input-output observations which may be expensive to obtain, while their predictions may not be consistent with the underlying physical principles that generated the observed data. In this work, we propose a novel model class coined as physics-informed DeepONets, which introduces an effective regularization mechanism for biasing the outputs of DeepOnet models towards ensuring physical consistency. This is accomplished by leveraging automatic differentiation to impose the underlying physical laws via soft penalty constraints during model training. We demonstrate that this simple, yet remarkably effective extension can not only yield a significant improvement in the predictive accuracy of DeepOnets, but also greatly reduce the need for large training data-sets. To this end, a remarkable observation is that physics-informed DeepONets are capable of solving parametric partial differential equations (PDEs) without any paired input-output observations, except for a set of given initial or boundary conditions. We illustrate the effectiveness of the proposed framework through a series of comprehensive numerical studies across various types of PDEs. Strikingly, a trained physics informed DeepOnet model can predict the solution of $\mathcal{O}(10^3)$ time-dependent PDEs in a fraction of a second -- up to three orders of magnitude faster compared a conventional PDE solver. The data and code accompanying this manuscript are publicly available at \url{https://github.com/PredictiveIntelligenceLab/Physics-informed-DeepONets}.
Gaussian processes meet NeuralODEs: A Bayesian framework for learning the dynamics of partially observed systems from scarce and noisy data
Mar 04, 2021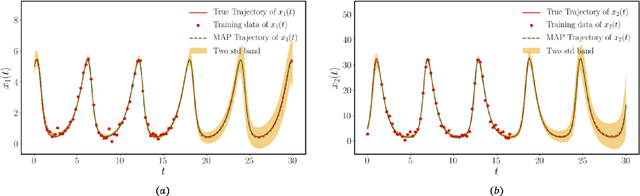

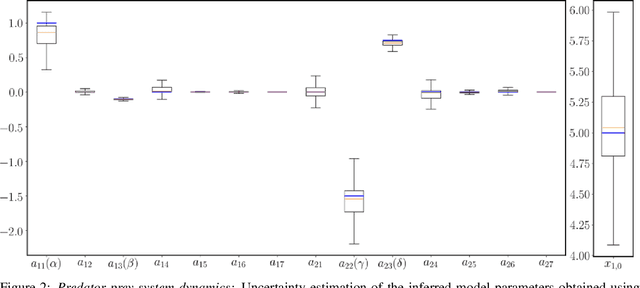

Abstract:This paper presents a machine learning framework (GP-NODE) for Bayesian systems identification from partial, noisy and irregular observations of nonlinear dynamical systems. The proposed method takes advantage of recent developments in differentiable programming to propagate gradient information through ordinary differential equation solvers and perform Bayesian inference with respect to unknown model parameters using Hamiltonian Monte Carlo sampling and Gaussian Process priors over the observed system states. This allows us to exploit temporal correlations in the observed data, and efficiently infer posterior distributions over plausible models with quantified uncertainty. Moreover, the use of sparsity-promoting priors such as the Finnish Horseshoe for free model parameters enables the discovery of interpretable and parsimonious representations for the underlying latent dynamics. A series of numerical studies is presented to demonstrate the effectiveness of the proposed GP-NODE method including predator-prey systems, systems biology, and a 50-dimensional human motion dynamical system. Taken together, our findings put forth a novel, flexible and robust workflow for data-driven model discovery under uncertainty. All code and data accompanying this manuscript are available online at \url{https://github.com/PredictiveIntelligenceLab/GP-NODEs}.
Learning atrial fiber orientations and conductivity tensors from intracardiac maps using physics-informed neural networks
Feb 22, 2021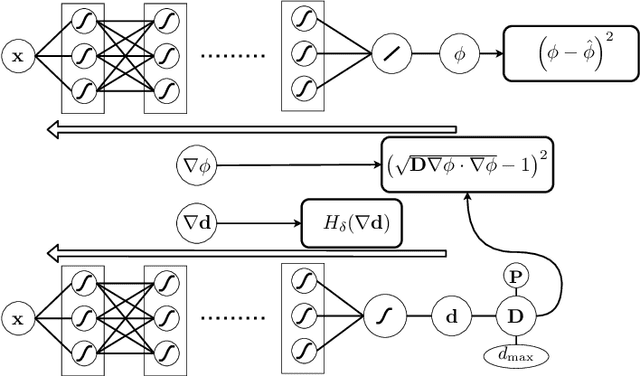
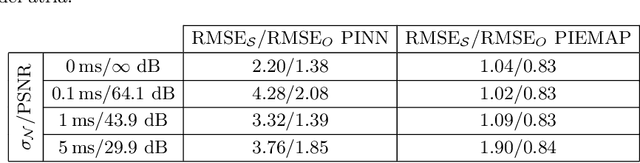
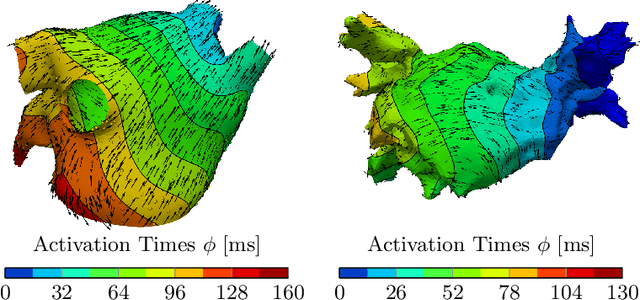
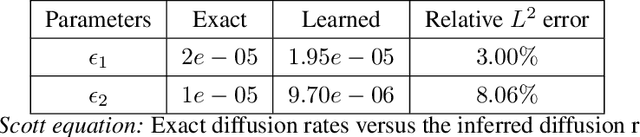
Abstract:Electroanatomical maps are a key tool in the diagnosis and treatment of atrial fibrillation. Current approaches focus on the activation times recorded. However, more information can be extracted from the available data. The fibers in cardiac tissue conduct the electrical wave faster, and their direction could be inferred from activation times. In this work, we employ a recently developed approach, called physics informed neural networks, to learn the fiber orientations from electroanatomical maps, taking into account the physics of the electrical wave propagation. In particular, we train the neural network to weakly satisfy the anisotropic eikonal equation and to predict the measured activation times. We use a local basis for the anisotropic conductivity tensor, which encodes the fiber orientation. The methodology is tested both in a synthetic example and for patient data. Our approach shows good agreement in both cases and it outperforms a state of the art method in the patient data. The results show a first step towards learning the fiber orientations from electroanatomical maps with physics-informed neural networks.
Output-Weighted Sampling for Multi-Armed Bandits with Extreme Payoffs
Feb 19, 2021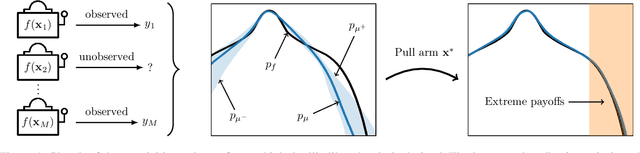
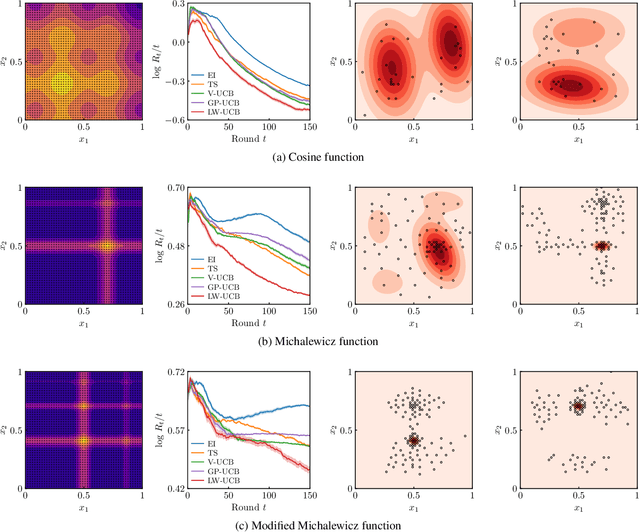
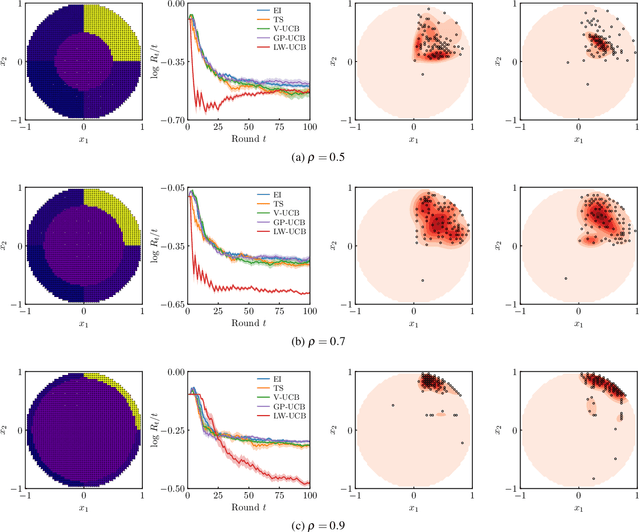
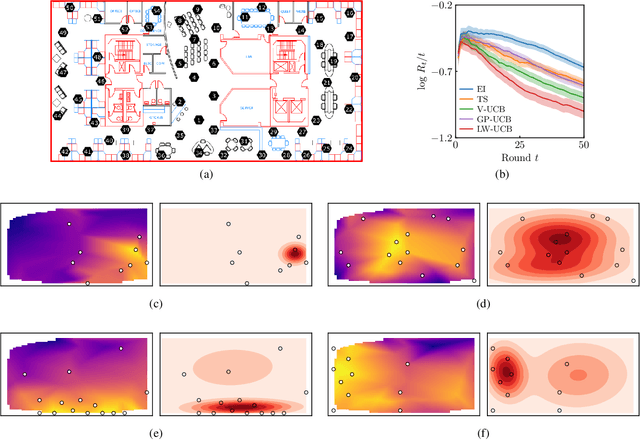
Abstract:We present a new type of acquisition functions for online decision making in multi-armed and contextual bandit problems with extreme payoffs. Specifically, we model the payoff function as a Gaussian process and formulate a novel type of upper confidence bound (UCB) acquisition function that guides exploration towards the bandits that are deemed most relevant according to the variability of the observed rewards. This is achieved by computing a tractable likelihood ratio that quantifies the importance of the output relative to the inputs and essentially acts as an \textit{attention mechanism} that promotes exploration of extreme rewards. We demonstrate the benefits of the proposed methodology across several synthetic benchmarks, as well as a realistic example involving noisy sensor network data. Finally, we provide a JAX library for efficient bandit optimization using Gaussian processes.
On the eigenvector bias of Fourier feature networks: From regression to solving multi-scale PDEs with physics-informed neural networks
Dec 18, 2020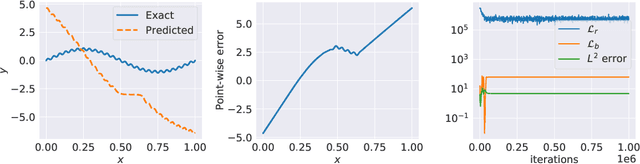
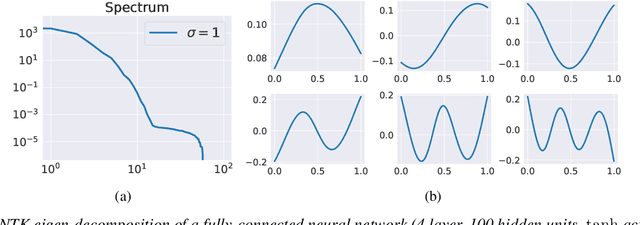
Abstract:Physics-informed neural networks (PINNs) are demonstrating remarkable promise in integrating physical models with gappy and noisy observational data, but they still struggle in cases where the target functions to be approximated exhibit high-frequency or multi-scale features. In this work we investigate this limitation through the lens of Neural Tangent Kernel (NTK) theory and elucidate how PINNs are biased towards learning functions along the dominant eigen-directions of their limiting NTK. Using this observation, we construct novel architectures that employ spatio-temporal and multi-scale random Fourier features, and justify how such coordinate embedding layers can lead to robust and accurate PINN models. Numerical examples are presented for several challenging cases where conventional PINN models fail, including wave propagation and reaction-diffusion dynamics, illustrating how the proposed methods can be used to effectively tackle both forward and inverse problems involving partial differential equations with multi-scale behavior. All code an data accompanying this manuscript will be made publicly available at \url{https://github.com/PredictiveIntelligenceLab/MultiscalePINNs}.
Learning Unknown Physics of non-Newtonian Fluids
Aug 26, 2020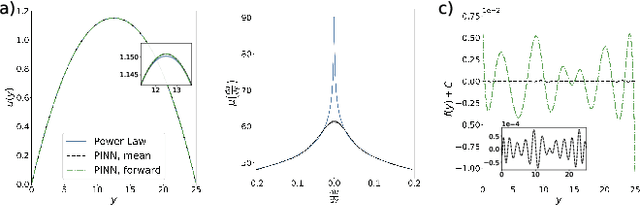
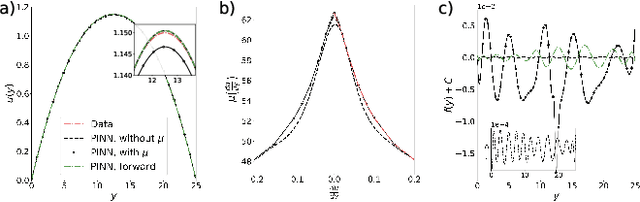
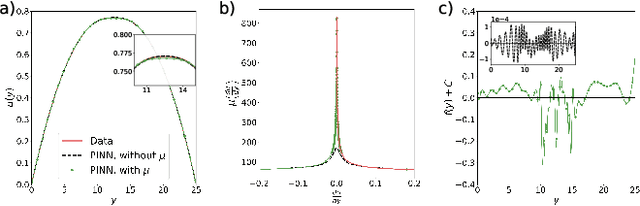
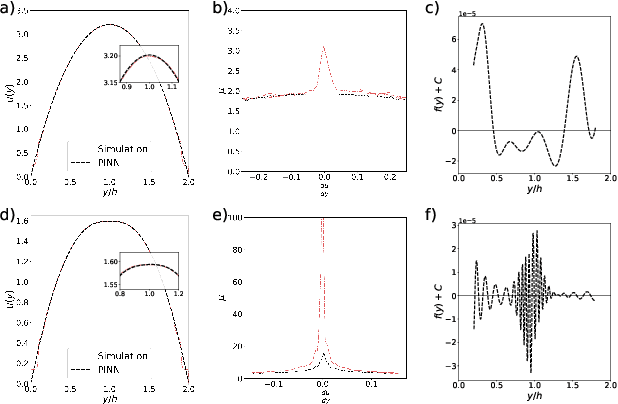
Abstract:We extend the physics-informed neural network (PINN) method to learn viscosity models of two non-Newtonian systems (polymer melts and suspensions of particles) using only velocity measurements. The PINN-inferred viscosity models agree with the empirical models for shear rates with large absolute values but deviate for shear rates near zero where the analytical models have an unphysical singularity. Once a viscosity model is learned, we use the PINN method to solve the momentum conservation equation for non-Newtonian fluid flow using only the boundary conditions.
When and why PINNs fail to train: A neural tangent kernel perspective
Jul 28, 2020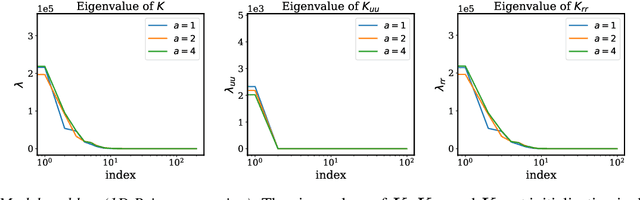
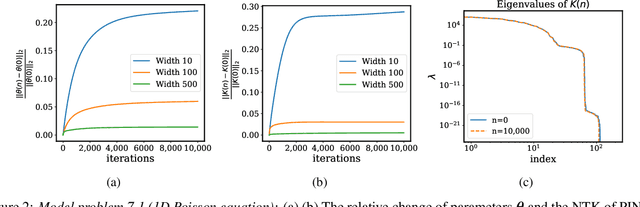
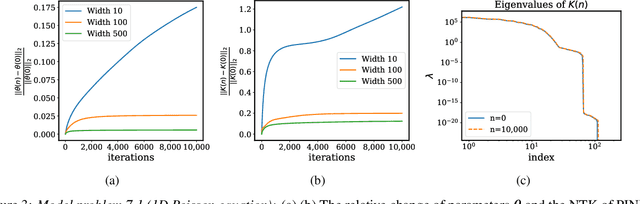
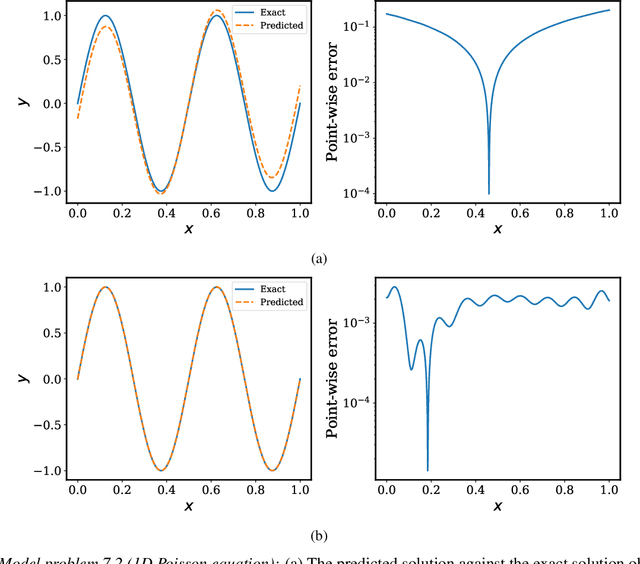
Abstract:Physics-informed neural networks (PINNs) have lately received great attention thanks to their flexibility in tackling a wide range of forward and inverse problems involving partial differential equations. However, despite their noticeable empirical success, little is known about how such constrained neural networks behave during their training via gradient descent. More importantly, even less is known about why such models sometimes fail to train at all. In this work, we aim to investigate these questions through the lens of the Neural Tangent Kernel (NTK); a kernel that captures the behavior of fully-connected neural networks in the infinite width limit during training via gradient descent. Specifically, we derive the NTK of PINNs and prove that, under appropriate conditions, it converges to a deterministic kernel that stays constant during training in the infinite-width limit. This allows us to analyze the training dynamics of PINNs through the lens of their limiting NTK and find a remarkable discrepancy in the convergence rate of the different loss components contributing to the total training error. To address this fundamental pathology, we propose a novel gradient descent algorithm that utilizes the eigenvalues of the NTK to adaptively calibrate the convergence rate of the total training error. Finally, we perform a series of numerical experiments to verify the correctness of our theory and the practical effectiveness of the proposed algorithms. The data and code accompanying this manuscript are publicly available at \url{https://github.com/PredictiveIntelligenceLab/PINNsNTK}.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge