Optimizing Resource Allocation for Geographically-Distributed Inference by Large Language Models

Large language models have demonstrated extraordinary performance in many AI tasks but are expensive to use, even after training, due to their requirement of high-end GPUs. Recently, a distributed system called PETALS was developed to lower the barrier for deploying LLMs by splitting the model blocks across multiple servers with low-end GPUs distributed over the Internet, which was much faster than swapping the model parameters between the GPU memory and other cheaper but slower local storage media. However, the performance of such a distributed system critically depends on the resource allocation, and how to do so optimally remains unknown. In this work, we present the first systematic study of the resource allocation problem in distributed LLM inference, with focus on two important decisions: block placement and request routing. Our main results include: experimentally validated performance models that can predict the inference performance under given block placement and request routing decisions, a formulation of the offline optimization of block placement and request routing as a mixed integer linear programming problem together with the NP-hardness proof and a polynomial-complexity algorithm with guaranteed performance, and an adaptation of the offline algorithm for the online setting with the same performance guarantee under bounded load. Through both experiments and experimentally-validated simulations, we have verified that the proposed solution can substantially reduce the inference time compared to the state-of-the-art solution in diverse settings with geographically-distributed servers. As a byproduct, we have also developed a light-weighted CPU-only simulator capable of predicting the performance of distributed LLM inference on GPU servers, which can evaluate large deployments and facilitate future research for researchers with limited GPU access.

Adaptive Stochastic Gradient Descent for Fast and Communication-Efficient Distributed Learning

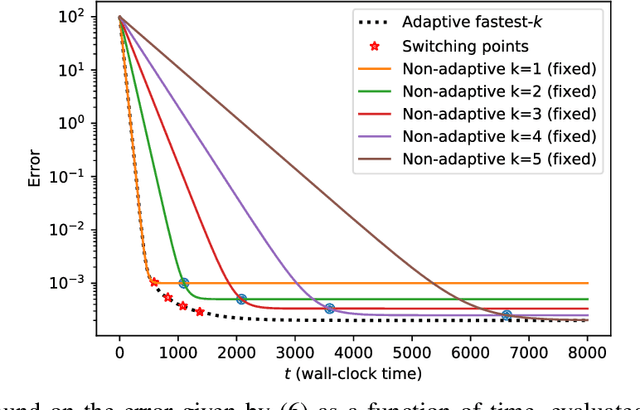
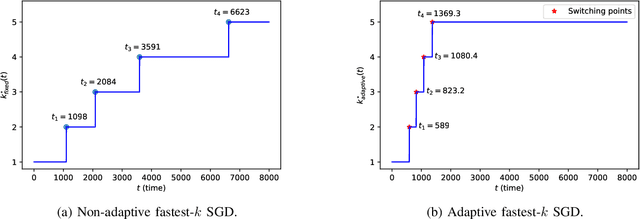
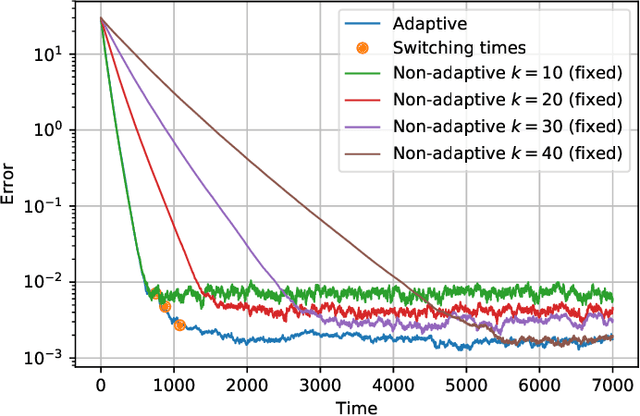
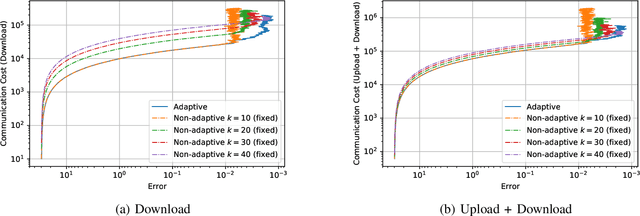
We consider the setting where a master wants to run a distributed stochastic gradient descent (SGD) algorithm on $n$ workers, each having a subset of the data. Distributed SGD may suffer from the effect of stragglers, i.e., slow or unresponsive workers who cause delays. One solution studied in the literature is to wait at each iteration for the responses of the fastest $k<n$ workers before updating the model, where $k$ is a fixed parameter. The choice of the value of $k$ presents a trade-off between the runtime (i.e., convergence rate) of SGD and the error of the model. Towards optimizing the error-runtime trade-off, we investigate distributed SGD with adaptive~$k$, i.e., varying $k$ throughout the runtime of the algorithm. We first design an adaptive policy for varying $k$ that optimizes this trade-off based on an upper bound on the error as a function of the wall-clock time that we derive. Then, we propose and implement an algorithm for adaptive distributed SGD that is based on a statistical heuristic. Our results show that the adaptive version of distributed SGD can reach lower error values in less time compared to non-adaptive implementations. Moreover, the results also show that the adaptive version is communication-efficient, where the amount of communication required between the master and the workers is less than that of non-adaptive versions.

Modeling Performance and Energy trade-offs in Online Data-Intensive Applications

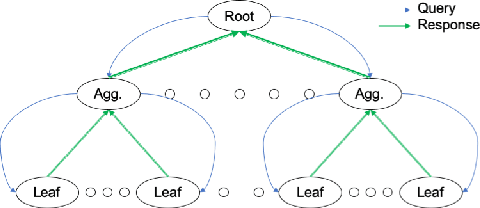
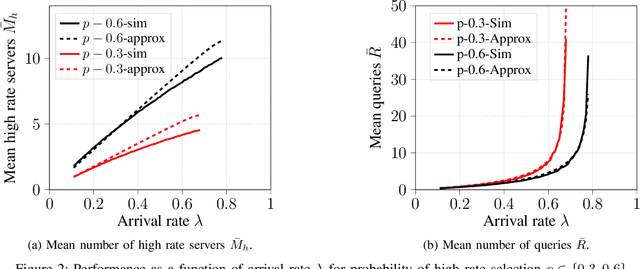
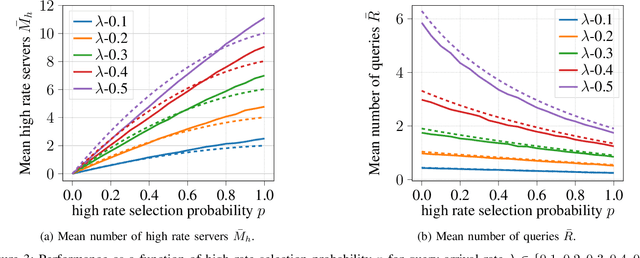
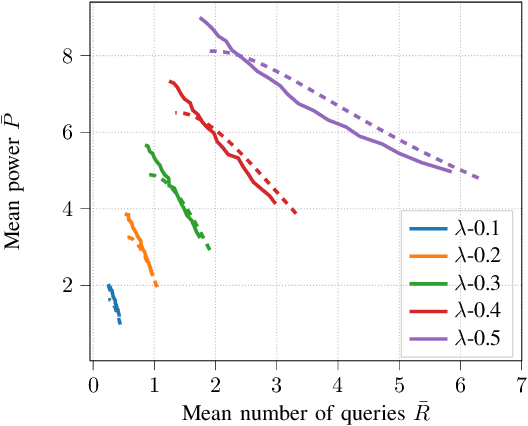
We consider energy minimization for data-intensive applications run on large number of servers, for given performance guarantees. We consider a system, where each incoming application is sent to a set of servers, and is considered to be completed if a subset of them finish serving it. We consider a simple case when each server core has two speed levels, where the higher speed can be achieved by higher power for each core independently. The core selects one of the two speeds probabilistically for each incoming application request. We model arrival of application requests by a Poisson process, and random service time at the server with independent exponential random variables. Our model and analysis generalizes to today's state-of-the-art in CPU energy management where each core can independently select a speed level from a set of supported speeds and corresponding voltages. The performance metrics under consideration are the mean number of applications in the system and the average energy expenditure. We first provide a tight approximation to study this previously intractable problem and derive closed form approximate expressions for the performance metrics when service times are exponentially distributed. Next, we study the trade-off between the approximate mean number of applications and energy expenditure in terms of the switching probability.

Adaptive Distributed Stochastic Gradient Descent for Minimizing Delay in the Presence of Stragglers

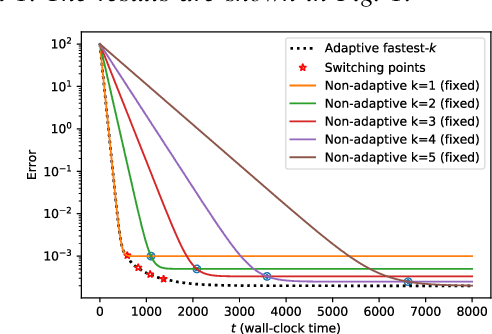
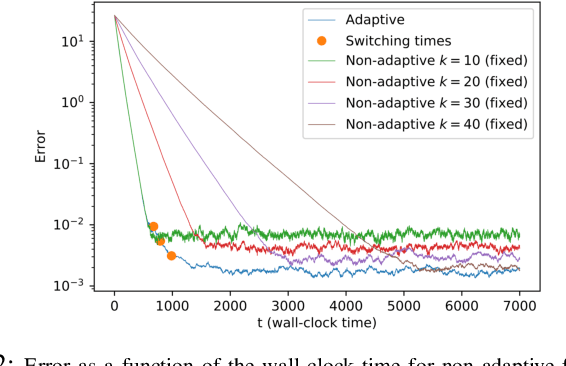
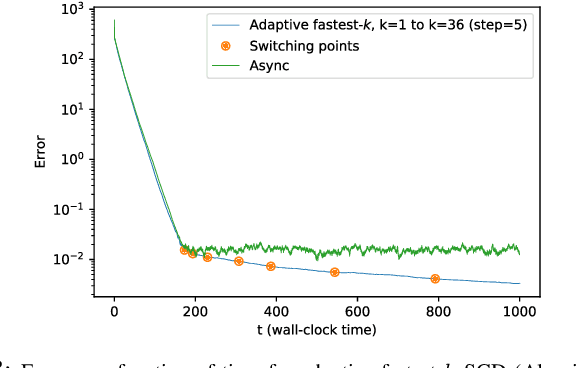
We consider the setting where a master wants to run a distributed stochastic gradient descent (SGD) algorithm on $n$ workers each having a subset of the data. Distributed SGD may suffer from the effect of stragglers, i.e., slow or unresponsive workers who cause delays. One solution studied in the literature is to wait at each iteration for the responses of the fastest $k<n$ workers before updating the model, where $k$ is a fixed parameter. The choice of the value of $k$ presents a trade-off between the runtime (i.e., convergence rate) of SGD and the error of the model. Towards optimizing the error-runtime trade-off, we investigate distributed SGD with adaptive $k$. We first design an adaptive policy for varying $k$ that optimizes this trade-off based on an upper bound on the error as a function of the wall-clock time which we derive. Then, we propose an algorithm for adaptive distributed SGD that is based on a statistical heuristic. We implement our algorithm and provide numerical simulations which confirm our intuition and theoretical analysis.