Understanding Anharmonic Effects on Hydrogen Desorption Characteristics of Mg$_n$H$_{2n}$ Nanoclusters by ab initio trained Deep Neural Network

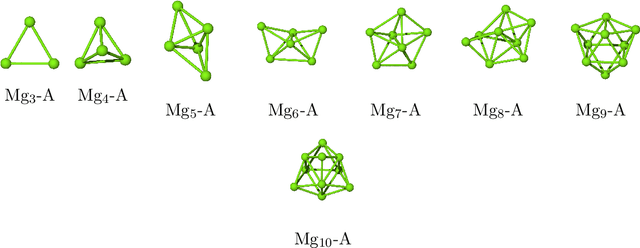
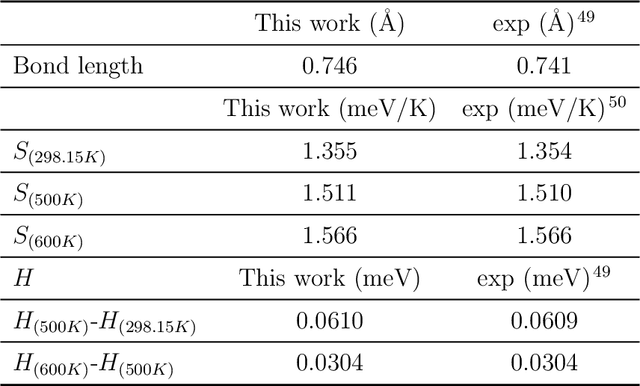
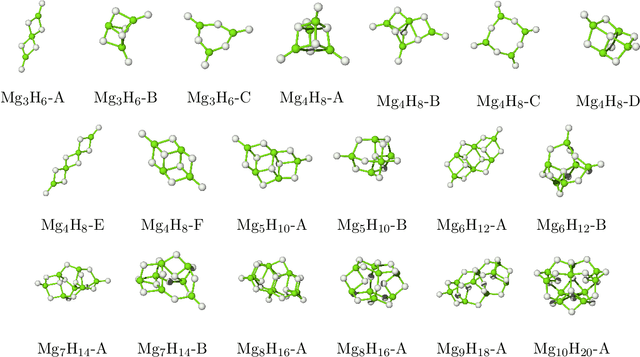
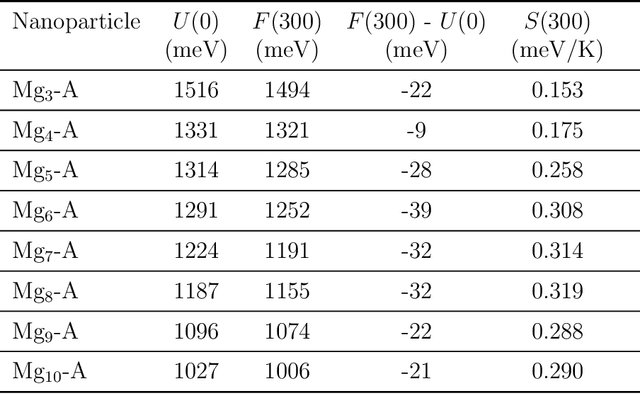
Magnesium hydride (MgH$_2$) has been widely studied for effective hydrogen storage. However, its bulk desorption temperature (553 K) is deemed too high for practical applications. Besides doping, a strategy to decrease such reaction energy for releasing hydrogen is the use of MgH$_2$-based nanoparticles (NPs). Here, we investigate first the thermodynamic properties of Mg$_n$H$_{2n}$ NPs ($n<10$) from first-principles, in particular by assessing the anharmonic effects on the enthalpy, entropy and thermal expansion by means of the Stochastic Self Consistent Harmonic Approximation (SSCHA). The latter method goes beyond previous approaches, typically based on molecular mechanics and the quasi-harmonic approximation, allowing the ab initio calculation of the fully-anharmonic free energy. We find an almost linear dependence on temperature of the interatomic bond lengths - with a relative variation of few percent over 300K -, alongside with a bond distance decrease of the Mg-H bonds. In order to increase the size of NPs toward experiments of hydrogen desorption from MgH$_2$ we devise a computationally effective Machine Learning model trained to accurately determine the forces and total energies (i.e. the potential energy surfaces), integrating the latter with the SSCHA model to fully include the anharmonic effects. We find a significative decrease of the H-desorption temperature for sub-nanometric clusters Mg$_n$H$_{2n}$ with $n \leq 10$, with a non-negligible, although little effect due to anharmonicities (up to 10%).

Expectation propagation: a probabilistic view of Deep Feed Forward Networks

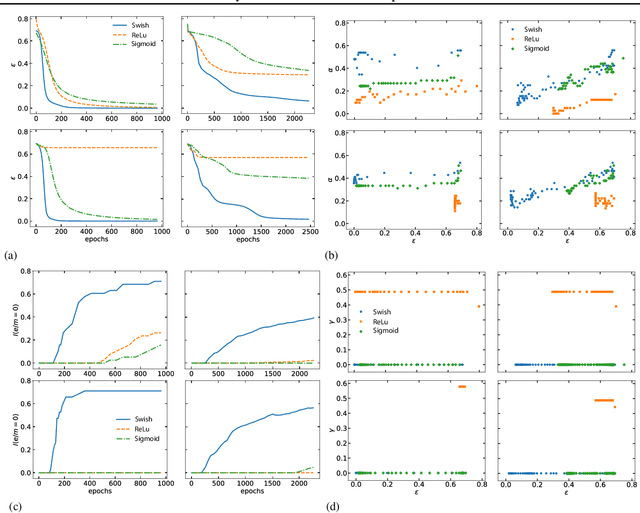
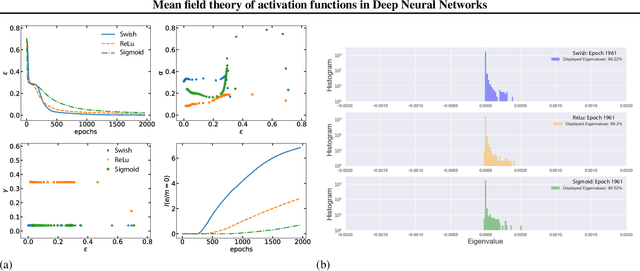
We present a statistical mechanics model of deep feed forward neural networks (FFN). Our energy-based approach naturally explains several known results and heuristics, providing a solid theoretical framework and new instruments for a systematic development of FFN. We infer that FFN can be understood as performing three basic steps: encoding, representation validation and propagation. We obtain a set of natural activations -- such as sigmoid, $\tanh$ and ReLu -- together with a state-of-the-art one, recently obtained by Ramachandran et al.(arXiv:1710.05941) using an extensive search algorithm. We term this activation ESP (Expected Signal Propagation), explain its probabilistic meaning, and study the eigenvalue spectrum of the associated Hessian on classification tasks. We find that ESP allows for faster training and more consistent performances over a wide range of network architectures.