Evolutionary Bi-objective Optimization for the Dynamic Chance-Constrained Knapsack Problem Based on Tail Bound Objectives

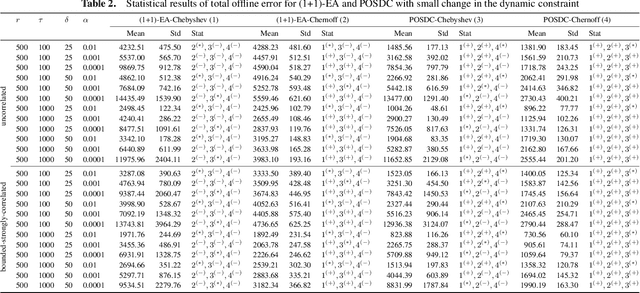
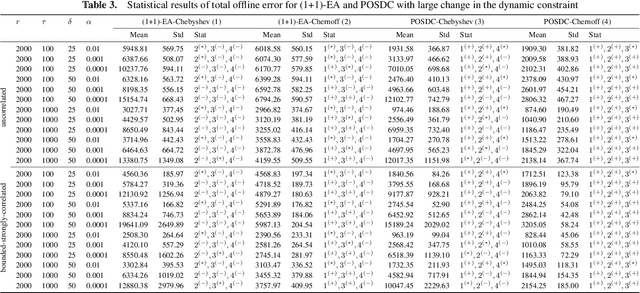
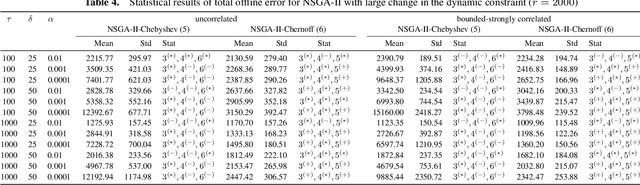
Real-world combinatorial optimization problems are often stochastic and dynamic. Therefore, it is essential to make optimal and reliable decisions with a holistic approach. In this paper, we consider the dynamic chance-constrained knapsack problem where the weight of each item is stochastic, the capacity constraint changes dynamically over time, and the objective is to maximize the total profit subject to the probability that total weight exceeds the capacity. We make use of prominent tail inequalities such as Chebyshev's inequality, and Chernoff bound to approximate the probabilistic constraint. Our key contribution is to introduce an additional objective which estimates the minimal capacity bound for a given stochastic solution that still meets the chance constraint. This objective helps to cater for dynamic changes to the stochastic problem. We apply single- and multi-objective evolutionary algorithms to the problem and show how bi-objective optimization can help to deal with dynamic chance-constrained problems.

Evolutionary Algorithms for the Chance-Constrained Knapsack Problem

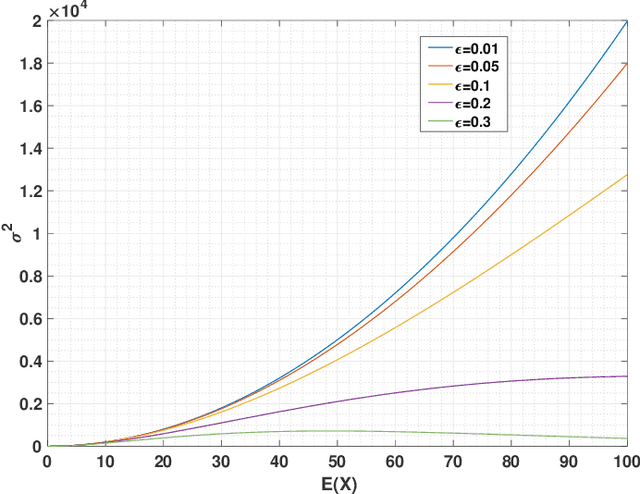
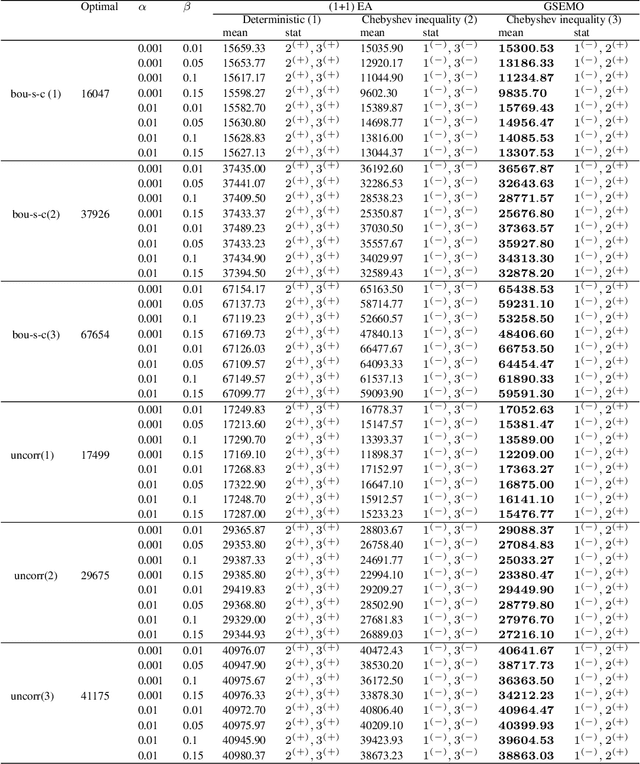
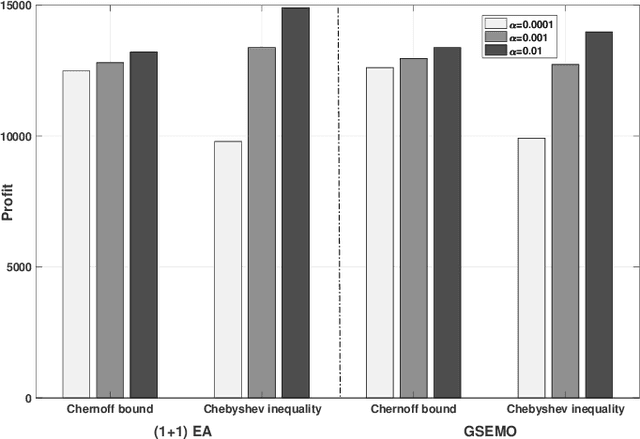
Evolutionary algorithms have been widely used for a range of stochastic optimization problems. In most studies, the goal is to optimize the expected quality of the solution. Motivated by real-world problems where constraint violations have extremely disruptive effects, we consider a variant of the knapsack problem where the profit is maximized under the constraint that the knapsack capacity bound is violated with a small probability of at most $\alpha$. This problem is known as chance-constrained knapsack problem and chance-constrained optimization problems have so far gained little attention in the evolutionary computation literature. We show how to use popular deviation inequalities such as Chebyshev's inequality and Chernoff bounds as part of the solution evaluation when tackling these problems by evolutionary algorithms and compare the effectiveness of our algorithms on a wide range of chance-constrained knapsack instances.