Run-of-Mine Stockyard Recovery Scheduling and Optimisation for Multiple Reclaimers

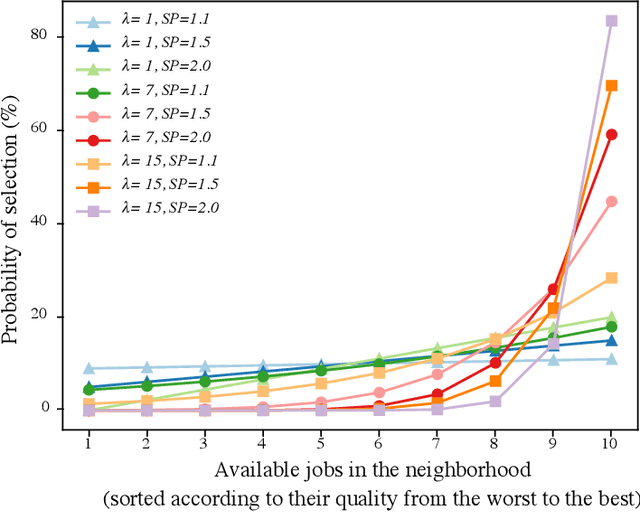
Stockpiles are essential in the mining value chain, assisting in maximising value and production. Quality control of taken minerals from the stockpiles is a major concern for stockpile managers where failure to meet some requirements can lead to losing money. This problem was recently investigated using a single reclaimer, and basic assumptions. This study extends the approach to consider multiple reclaimers in preparing for short and long-term deliveries. The engagement of multiple reclaimers complicates the problem in terms of their interaction in preparing a delivery simultaneously and safety distancing of reclaimers. We also consider more realistic settings, such as handling different minerals with different types of reclaimers. We propose methods that construct a solution step by step to meet precedence constraints for all reclaimers in the stockyard. We study various instances of the problem using greedy algorithms, Ant Colony Optimisation (ACO), and propose an integrated local search method determining an efficient schedule. We fine-tune and compare the algorithms and show that the ACO combined with local search can yield efficient solutions.

Novelty-Driven Binary Particle Swarm Optimisation for Truss Optimisation Problems

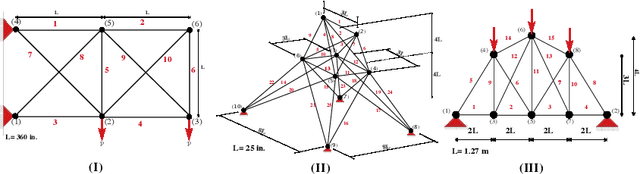
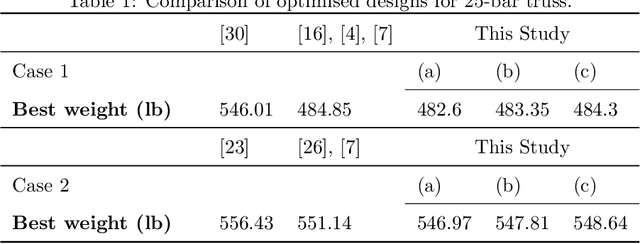
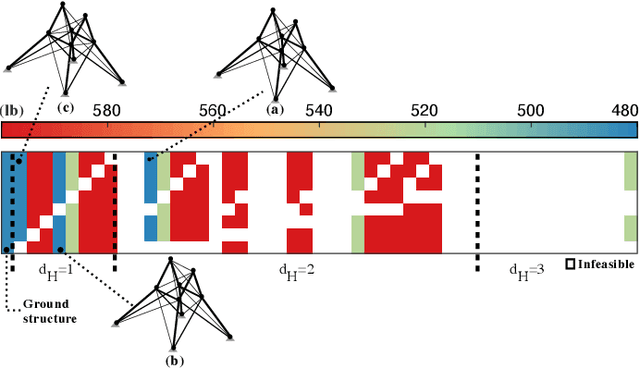
Topology optimisation of trusses can be formulated as a combinatorial and multi-modal problem in which locating distinct optimal designs allows practitioners to choose the best design based on their preferences. Bilevel optimisation has been successfully applied to truss optimisation to consider topology and sizing in upper and lower levels, respectively. We introduce exact enumeration to rigorously analyse the topology search space and remove randomness for small problems. We also propose novelty-driven binary particle swarm optimisation for bigger problems to discover new designs at the upper level by maximising novelty. For the lower level, we employ a reliable evolutionary optimiser to tackle the layout configuration aspect of the problem. We consider truss optimisation problem instances where designers need to select the size of bars from a discrete set with respect to practice code constraints. Our experimental investigations show that our approach outperforms the current state-of-the-art methods and it obtains multiple high-quality solutions.

Evolutionary Bi-objective Optimization for the Dynamic Chance-Constrained Knapsack Problem Based on Tail Bound Objectives

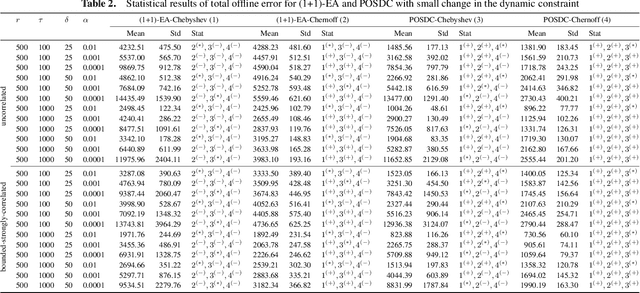
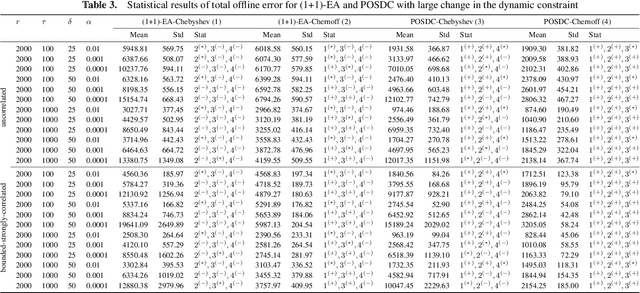
Real-world combinatorial optimization problems are often stochastic and dynamic. Therefore, it is essential to make optimal and reliable decisions with a holistic approach. In this paper, we consider the dynamic chance-constrained knapsack problem where the weight of each item is stochastic, the capacity constraint changes dynamically over time, and the objective is to maximize the total profit subject to the probability that total weight exceeds the capacity. We make use of prominent tail inequalities such as Chebyshev's inequality, and Chernoff bound to approximate the probabilistic constraint. Our key contribution is to introduce an additional objective which estimates the minimal capacity bound for a given stochastic solution that still meets the chance constraint. This objective helps to cater for dynamic changes to the stochastic problem. We apply single- and multi-objective evolutionary algorithms to the problem and show how bi-objective optimization can help to deal with dynamic chance-constrained problems.

Evolutionary Algorithms for the Chance-Constrained Knapsack Problem

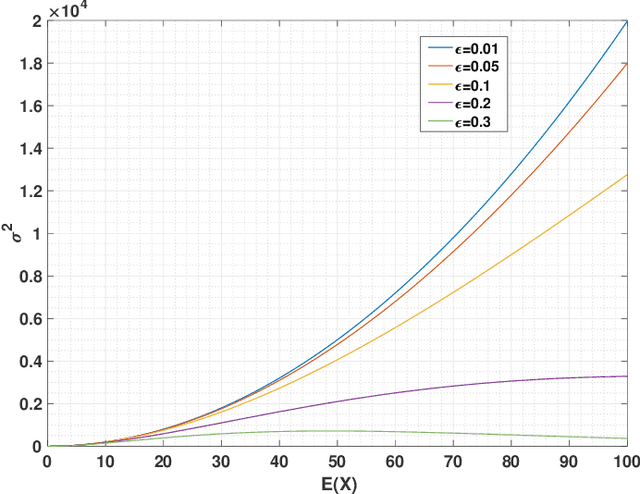
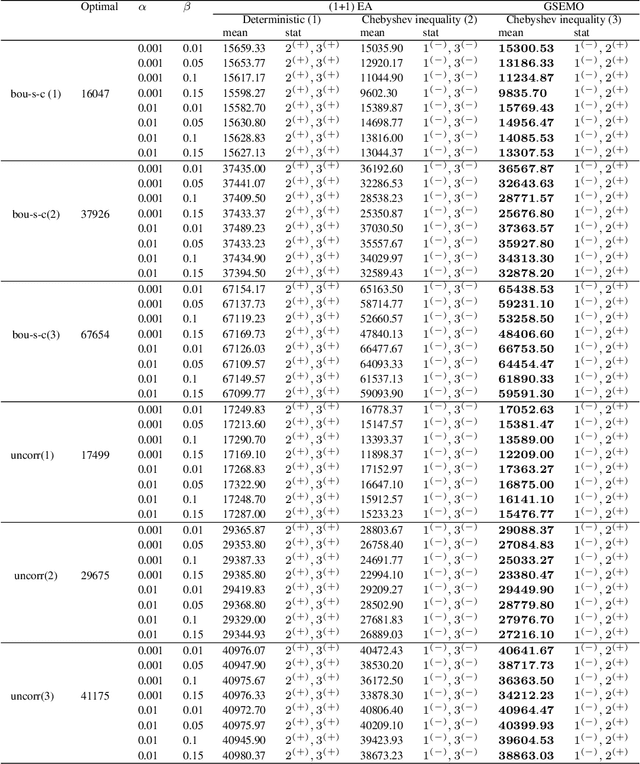
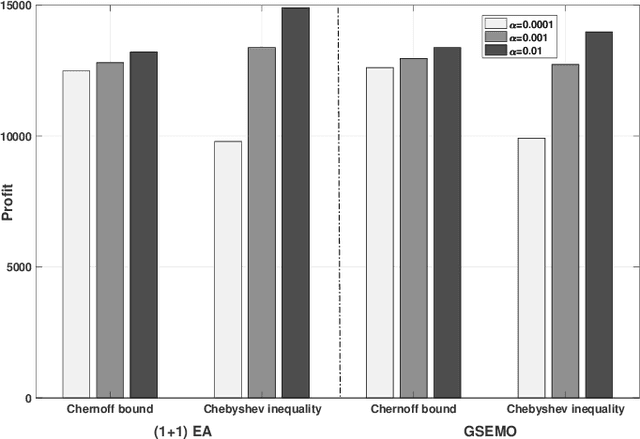
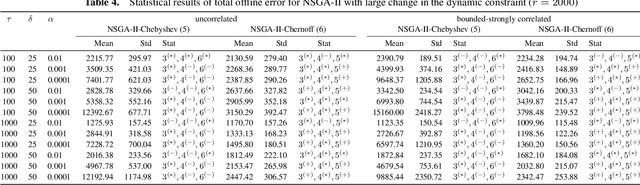
Evolutionary algorithms have been widely used for a range of stochastic optimization problems. In most studies, the goal is to optimize the expected quality of the solution. Motivated by real-world problems where constraint violations have extremely disruptive effects, we consider a variant of the knapsack problem where the profit is maximized under the constraint that the knapsack capacity bound is violated with a small probability of at most $\alpha$. This problem is known as chance-constrained knapsack problem and chance-constrained optimization problems have so far gained little attention in the evolutionary computation literature. We show how to use popular deviation inequalities such as Chebyshev's inequality and Chernoff bounds as part of the solution evaluation when tackling these problems by evolutionary algorithms and compare the effectiveness of our algorithms on a wide range of chance-constrained knapsack instances.