Two Birds with One Network: Unifying Failure Event Prediction and Time-to-failure Modeling

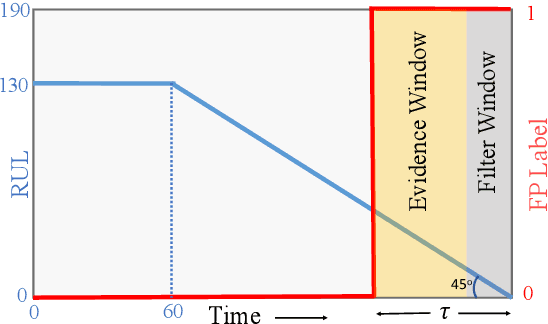
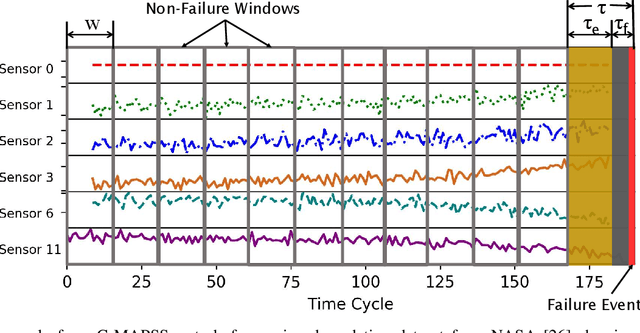
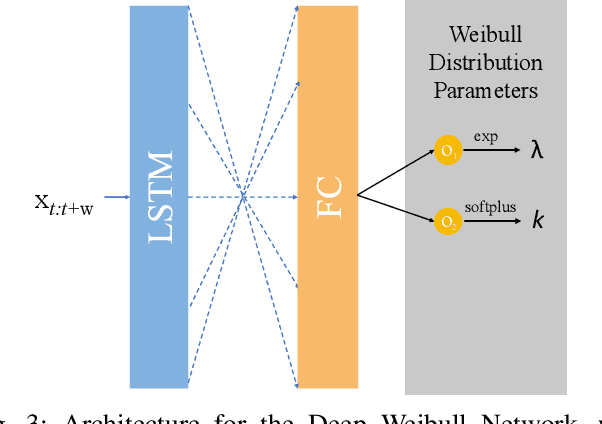
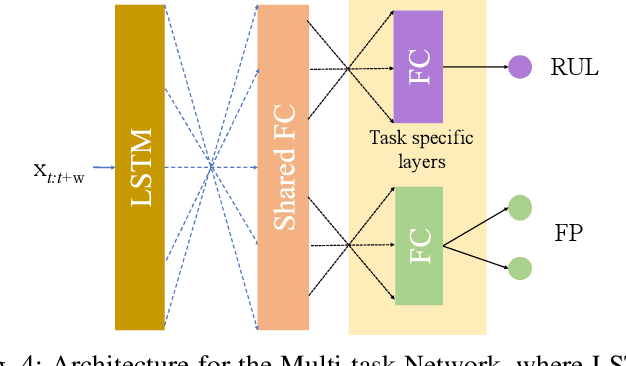
One of the key challenges in predictive maintenance is to predict the impending downtime of an equipment with a reasonable prediction horizon so that countermeasures can be put in place. Classically, this problem has been posed in two different ways which are typically solved independently: (1) Remaining useful life (RUL) estimation as a long-term prediction task to estimate how much time is left in the useful life of the equipment and (2) Failure prediction (FP) as a short-term prediction task to assess the probability of a failure within a pre-specified time window. As these two tasks are related, performing them separately is sub-optimal and might results in inconsistent predictions for the same equipment. In order to alleviate these issues, we propose two methods: Deep Weibull model (DW-RNN) and multi-task learning (MTL-RNN). DW-RNN is able to learn the underlying failure dynamics by fitting Weibull distribution parameters using a deep neural network, learned with a survival likelihood, without training directly on each task. While DW-RNN makes an explicit assumption on the data distribution, MTL-RNN exploits the implicit relationship between the long-term RUL and short-term FP tasks to learn the underlying distribution. Additionally, both our methods can leverage the non-failed equipment data for RUL estimation. We demonstrate that our methods consistently outperform baseline RUL methods that can be used for FP while producing consistent results for RUL and FP. We also show that our methods perform at par with baselines trained on the objectives optimized for either of the two tasks.

Constructing Effective Personalized Policies Using Counterfactual Inference from Biased Data Sets with Many Features

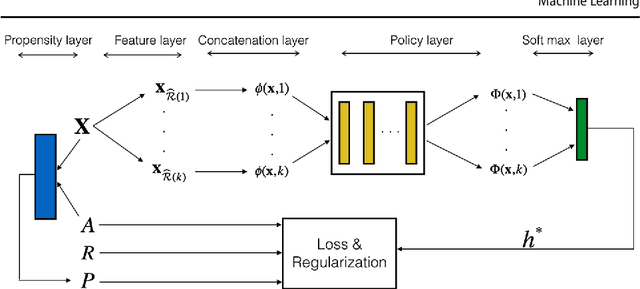
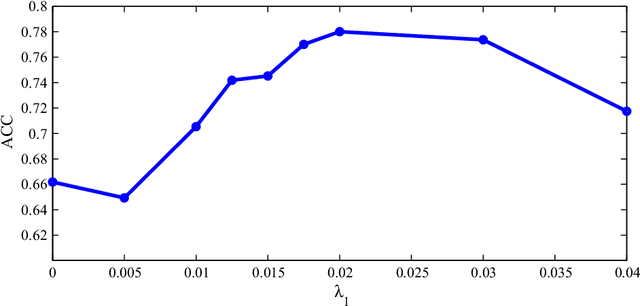
This paper proposes a novel approach for constructing effective personalized policies when the observed data lacks counter-factual information, is biased and possesses many features. The approach is applicable in a wide variety of settings from healthcare to advertising to education to finance. These settings have in common that the decision maker can observe, for each previous instance, an array of features of the instance, the action taken in that instance, and the reward realized -- but not the rewards of actions that were not taken: the counterfactual information. Learning in such settings is made even more difficult because the observed data is typically biased by the existing policy (that generated the data) and because the array of features that might affect the reward in a particular instance -- and hence should be taken into account in deciding on an action in each particular instance -- is often vast. The approach presented here estimates propensity scores for the observed data, infers counterfactuals, identifies a (relatively small) number of features that are (most) relevant for each possible action and instance, and prescribes a policy to be followed. Comparison of the proposed algorithm against the state-of-art algorithm on actual datasets demonstrates that the proposed algorithm achieves a significant improvement in performance.

Global Bandits

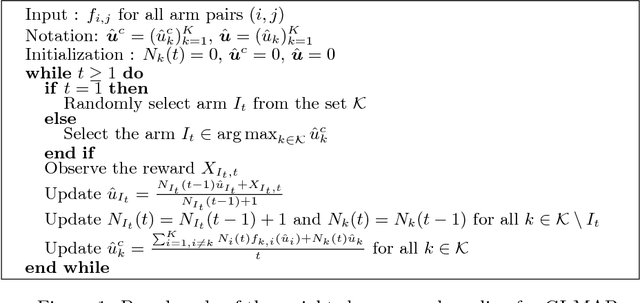
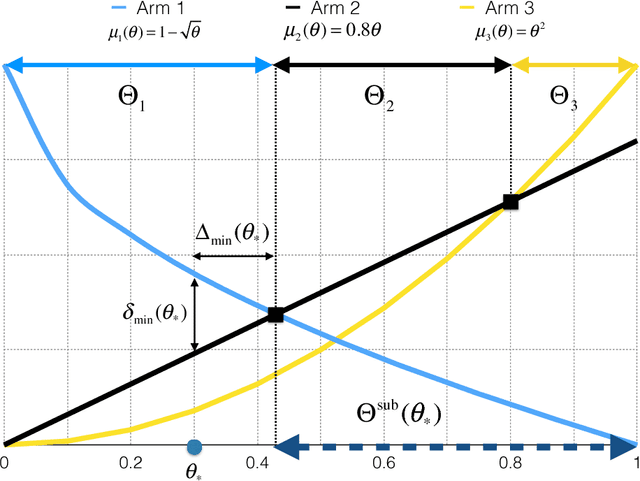
Multi-armed bandits (MAB) model sequential decision making problems, in which a learner sequentially chooses arms with unknown reward distributions in order to maximize its cumulative reward. Most of the prior work on MAB assumes that the reward distributions of each arm are independent. But in a wide variety of decision problems -- from drug dosage to dynamic pricing -- the expected rewards of different arms are correlated, so that selecting one arm provides information about the expected rewards of other arms as well. We propose and analyze a class of models of such decision problems, which we call {\em global bandits}. In the case in which rewards of all arms are deterministic functions of a single unknown parameter, we construct a greedy policy that achieves {\em bounded regret}, with a bound that depends on the single true parameter of the problem. Hence, this policy selects suboptimal arms only finitely many times with probability one. For this case we also obtain a bound on regret that is {\em independent of the true parameter}; this bound is sub-linear, with an exponent that depends on the informativeness of the arms. We also propose a variant of the greedy policy that achieves $\tilde{\mathcal{O}}(\sqrt{T})$ worst-case and $\mathcal{O}(1)$ parameter dependent regret. Finally, we perform experiments on dynamic pricing and show that the proposed algorithms achieve significant gains with respect to the well-known benchmarks.

Learning Optimal Policies from Observational Data

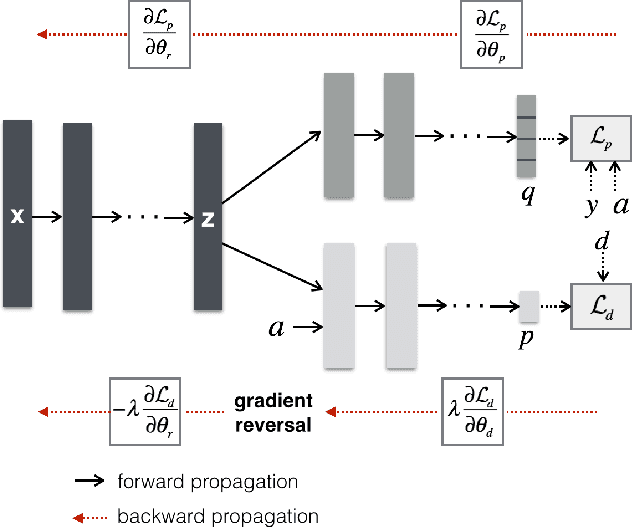
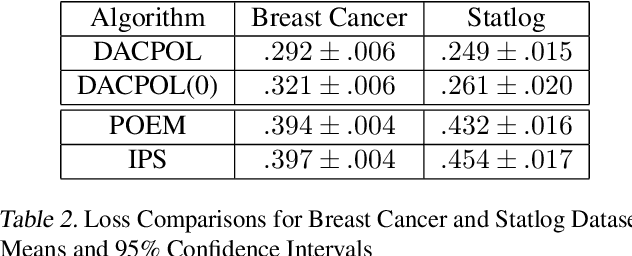
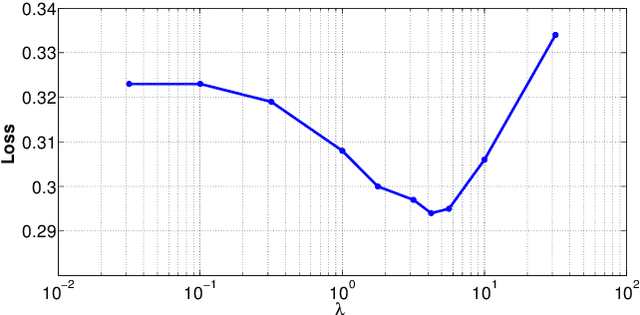
Choosing optimal (or at least better) policies is an important problem in domains from medicine to education to finance and many others. One approach to this problem is through controlled experiments/trials - but controlled experiments are expensive. Hence it is important to choose the best policies on the basis of observational data. This presents two difficult challenges: (i) missing counterfactuals, and (ii) selection bias. This paper presents theoretical bounds on estimation errors of counterfactuals from observational data by making connections to domain adaptation theory. It also presents a principled way of choosing optimal policies using domain adversarial neural networks. We illustrate the effectiveness of domain adversarial training together with various features of our algorithm on a semi-synthetic breast cancer dataset and a supervised UCI dataset (Statlog).

Data-Driven Online Decision Making with Costly Information Acquisition

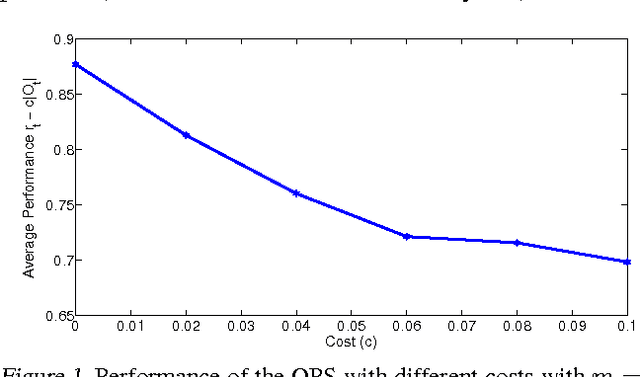
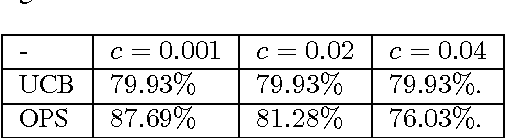
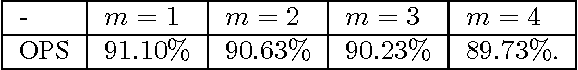
In most real-world settings such as recommender systems, finance, and healthcare, collecting useful information is costly and requires an active choice on the part of the decision maker. The decision-maker needs to learn simultaneously what observations to make and what actions to take. This paper incorporates the information acquisition decision into an online learning framework. We propose two different algorithms for this dual learning problem: Sim-OOS and Seq-OOS where observations are made simultaneously and sequentially, respectively. We prove that both algorithms achieve a regret that is sublinear in time. The developed framework and algorithms can be used in many applications including medical informatics, recommender systems and actionable intelligence in transportation, finance, cyber-security etc., in which collecting information prior to making decisions is costly. We validate our algorithms in a breast cancer example setting in which we show substantial performance gains for our proposed algorithms.

Context-Aware Proactive Content Caching with Service Differentiation in Wireless Networks

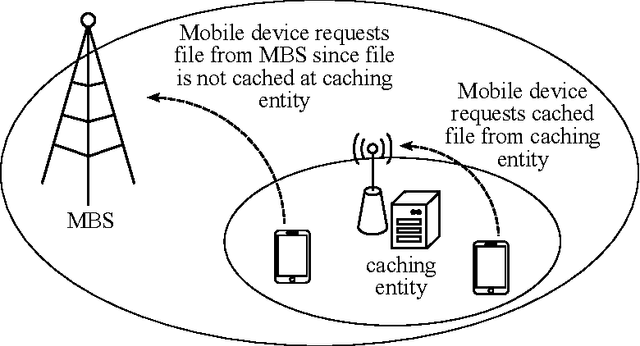
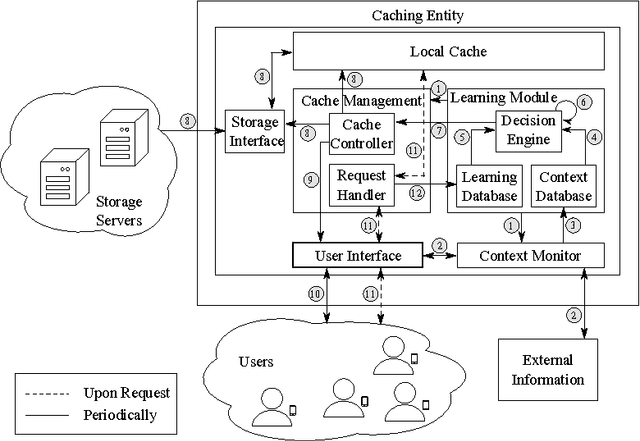
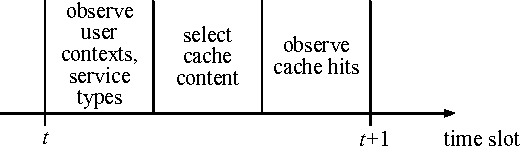
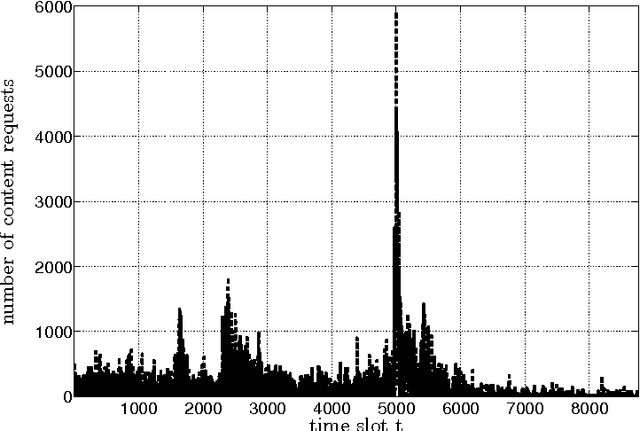
Content caching in small base stations or wireless infostations is considered to be a suitable approach to improve the efficiency in wireless content delivery. Placing the optimal content into local caches is crucial due to storage limitations, but it requires knowledge about the content popularity distribution, which is often not available in advance. Moreover, local content popularity is subject to fluctuations since mobile users with different interests connect to the caching entity over time. Which content a user prefers may depend on the user's context. In this paper, we propose a novel algorithm for context-aware proactive caching. The algorithm learns context-specific content popularity online by regularly observing context information of connected users, updating the cache content and observing cache hits subsequently. We derive a sublinear regret bound, which characterizes the learning speed and proves that our algorithm converges to the optimal cache content placement strategy in terms of maximizing the number of cache hits. Furthermore, our algorithm supports service differentiation by allowing operators of caching entities to prioritize customer groups. Our numerical results confirm that our algorithm outperforms state-of-the-art algorithms in a real world data set, with an increase in the number of cache hits of at least 14%.

Predicting Grades

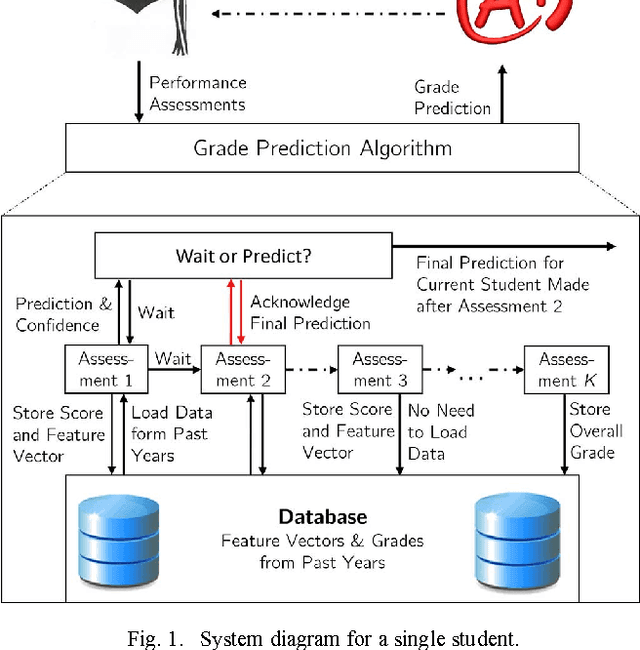
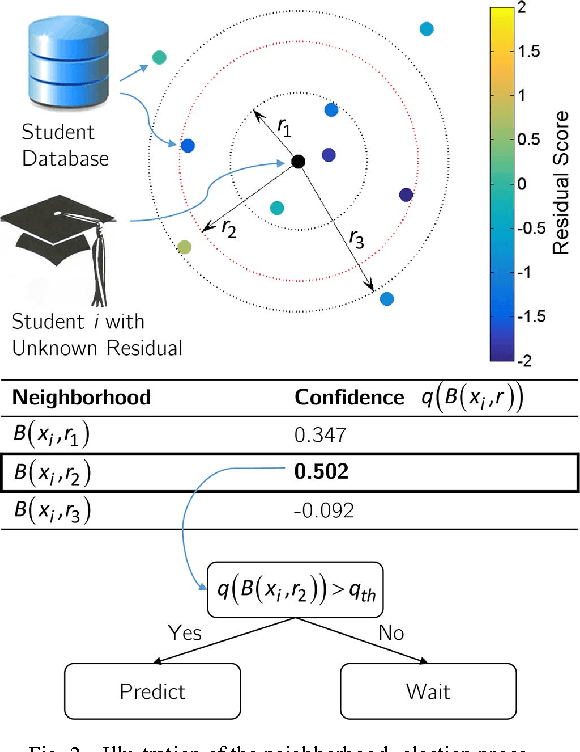
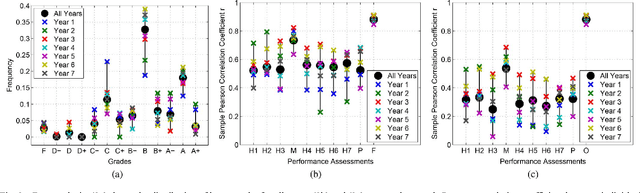
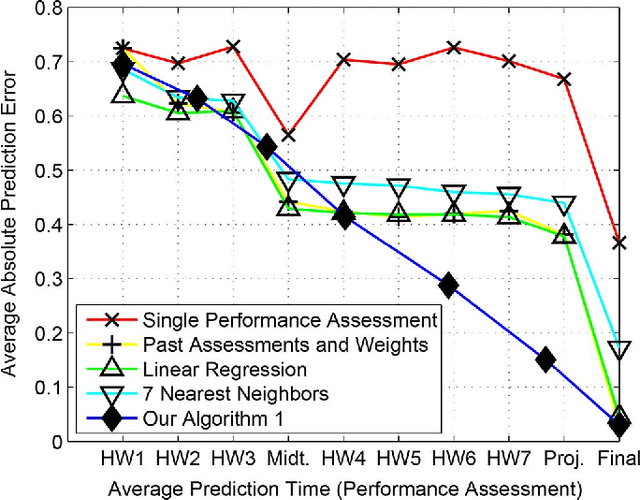
To increase efficacy in traditional classroom courses as well as in Massive Open Online Courses (MOOCs), automated systems supporting the instructor are needed. One important problem is to automatically detect students that are going to do poorly in a course early enough to be able to take remedial actions. Existing grade prediction systems focus on maximizing the accuracy of the prediction while overseeing the importance of issuing timely and personalized predictions. This paper proposes an algorithm that predicts the final grade of each student in a class. It issues a prediction for each student individually, when the expected accuracy of the prediction is sufficient. The algorithm learns online what is the optimal prediction and time to issue a prediction based on past history of students' performance in a course. We derive a confidence estimate for the prediction accuracy and demonstrate the performance of our algorithm on a dataset obtained based on the performance of approximately 700 UCLA undergraduate students who have taken an introductory digital signal processing over the past 7 years. We demonstrate that for 85% of the students we can predict with 76% accuracy whether they are going do well or poorly in the class after the 4th course week. Using data obtained from a pilot course, our methodology suggests that it is effective to perform early in-class assessments such as quizzes, which result in timely performance prediction for each student, thereby enabling timely interventions by the instructor (at the student or class level) when necessary.

Global Bandits with Holder Continuity

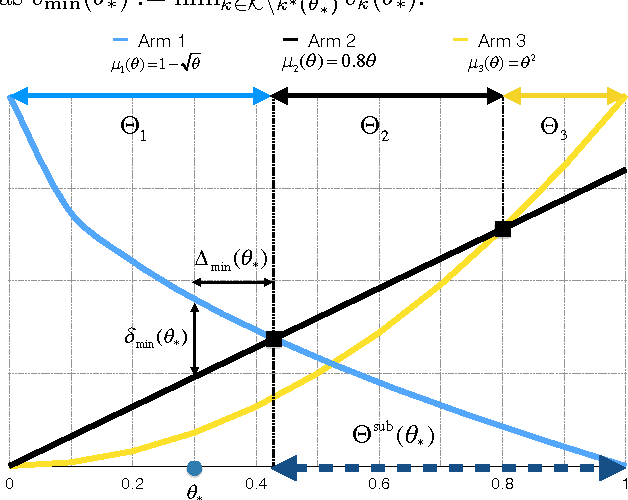
Standard Multi-Armed Bandit (MAB) problems assume that the arms are independent. However, in many application scenarios, the information obtained by playing an arm provides information about the remainder of the arms. Hence, in such applications, this informativeness can and should be exploited to enable faster convergence to the optimal solution. In this paper, we introduce and formalize the Global MAB (GMAB), in which arms are globally informative through a global parameter, i.e., choosing an arm reveals information about all the arms. We propose a greedy policy for the GMAB which always selects the arm with the highest estimated expected reward, and prove that it achieves bounded parameter-dependent regret. Hence, this policy selects suboptimal arms only finitely many times, and after a finite number of initial time steps, the optimal arm is selected in all of the remaining time steps with probability one. In addition, we also study how the informativeness of the arms about each other's rewards affects the speed of learning. Specifically, we prove that the parameter-free (worst-case) regret is sublinear in time, and decreases with the informativeness of the arms. We also prove a sublinear in time Bayesian risk bound for the GMAB which reduces to the well-known Bayesian risk bound for linearly parameterized bandits when the arms are fully informative. GMABs have applications ranging from drug and treatment discovery to dynamic pricing.