Adaptive Symmetrization of the KL Divergence

Many tasks in machine learning can be described as or reduced to learning a probability distribution given a finite set of samples. A common approach is to minimize a statistical divergence between the (empirical) data distribution and a parameterized distribution, e.g., a normalizing flow (NF) or an energy-based model (EBM). In this context, the forward KL divergence is a ubiquitous due to its tractability, though its asymmetry may prevent capturing some properties of the target distribution. Symmetric alternatives involve brittle min-max formulations and adversarial training (e.g., generative adversarial networks) or evaluating the reverse KL divergence, as is the case for the symmetric Jeffreys divergence, which is challenging to compute from samples. This work sets out to develop a new approach to minimize the Jeffreys divergence. To do so, it uses a proxy model whose goal is not only to fit the data, but also to assist in optimizing the Jeffreys divergence of the main model. This joint training task is formulated as a constrained optimization problem to obtain a practical algorithm that adapts the models priorities throughout training. We illustrate how this framework can be used to combine the advantages of NFs and EBMs in tasks such as density estimation, image generation, and simulation-based inference.

The Role of Learning Algorithms in Collective Action

Collective action in Machine Learning is the study of the control that a coordinated group can have over machine learning algorithms. While previous research has concentrated on assessing the impact of collectives against Bayes optimal classifiers, this perspective is limited, given that in reality, classifiers seldom achieve Bayes optimality and are influenced by the choice of learning algorithms along with their inherent inductive biases. In this work, we initiate the study of how the choice of the learning algorithm plays a role in the success of a collective in practical settings. Specifically, we focus on distributionally robust algorithms (DRO), popular for improving a worst group error, and on the popular stochastic gradient descent (SGD), due to its inductive bias for "simpler" functions. Our empirical results, supported by a theoretical foundation, show that the effective size and success of the collective are highly dependent on properties of the learning algorithm. This highlights the necessity of taking the learning algorithm into account when studying the impact of collective action in Machine learning.

Adversarial Likelihood Estimation with One-way Flows

Generative Adversarial Networks (GANs) can produce high-quality samples, but do not provide an estimate of the probability density around the samples. However, it has been noted that maximizing the log-likelihood within an energy-based setting can lead to an adversarial framework where the discriminator provides unnormalized density (often called energy). We further develop this perspective, incorporate importance sampling, and show that 1) Wasserstein GAN performs a biased estimate of the partition function, and we propose instead to use an unbiased estimator; 2) when optimizing for likelihood, one must maximize generator entropy. This is hypothesized to provide a better mode coverage. Different from previous works, we explicitly compute the density of the generated samples. This is the key enabler to designing an unbiased estimator of the partition function and computation of the generator entropy term. The generator density is obtained via a new type of flow network, called one-way flow network, that is less constrained in terms of architecture, as it does not require to have a tractable inverse function. Our experimental results show that we converge faster, produce comparable sample quality to GANs with similar architecture, successfully avoid over-fitting to commonly used datasets and produce smooth low-dimensional latent representations of the training data.

LED: Latent Variable-based Estimation of Density

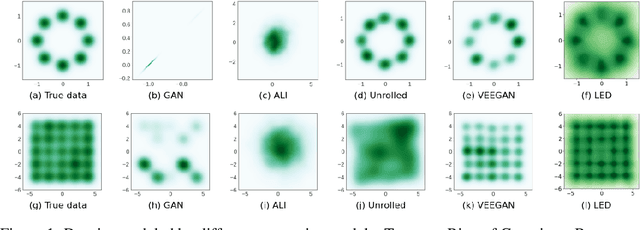
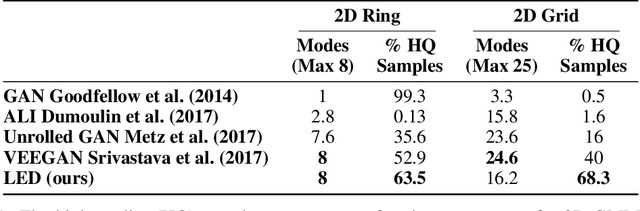
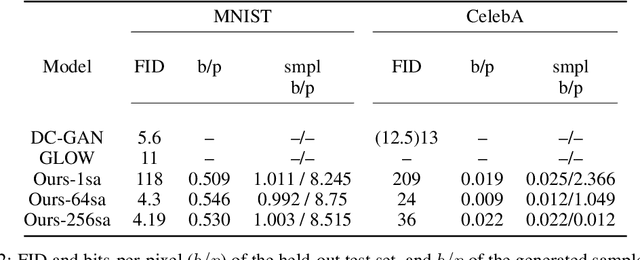
Modern generative models are roughly divided into two main categories: (1) models that can produce high-quality random samples, but cannot estimate the exact density of new data points and (2) those that provide exact density estimation, at the expense of sample quality and compactness of the latent space. In this work we propose LED, a new generative model closely related to GANs, that allows not only efficient sampling but also efficient density estimation. By maximizing log-likelihood on the output of the discriminator, we arrive at an alternative adversarial optimization objective that encourages generated data diversity. This formulation provides insights into the relationships between several popular generative models. Additionally, we construct a flow-based generator that can compute exact probabilities for generated samples, while allowing low-dimensional latent variables as input. Our experimental results, on various datasets, show that our density estimator produces accurate estimates, while retaining good quality in the generated samples.