Improved Uncertainty Quantification in Physics-Informed Neural Networks Using Error Bounds and Solution Bundles

Physics-Informed Neural Networks (PINNs) have been widely used to obtain solutions to various physical phenomena modeled as Differential Equations. As PINNs are not naturally equipped with mechanisms for Uncertainty Quantification, some work has been done to quantify the different uncertainties that arise when dealing with PINNs. In this paper, we use a two-step procedure to train Bayesian Neural Networks that provide uncertainties over the solutions to differential equation systems provided by PINNs. We use available error bounds over PINNs to formulate a heteroscedastic variance that improves the uncertainty estimation. Furthermore, we solve forward problems and utilize the obtained uncertainties when doing parameter estimation in inverse problems in cosmology.

Error-Aware B-PINNs: Improving Uncertainty Quantification in Bayesian Physics-Informed Neural Networks

Physics-Informed Neural Networks (PINNs) are gaining popularity as a method for solving differential equations. While being more feasible in some contexts than the classical numerical techniques, PINNs still lack credibility. A remedy for that can be found in Uncertainty Quantification (UQ) which is just beginning to emerge in the context of PINNs. Assessing how well the trained PINN complies with imposed differential equation is the key to tackling uncertainty, yet there is lack of comprehensive methodology for this task. We propose a framework for UQ in Bayesian PINNs (B-PINNs) that incorporates the discrepancy between the B-PINN solution and the unknown true solution. We exploit recent results on error bounds for PINNs on linear dynamical systems and demonstrate the predictive uncertainty on a class of linear ODEs.

Uncertainty Quantification in Neural Differential Equations

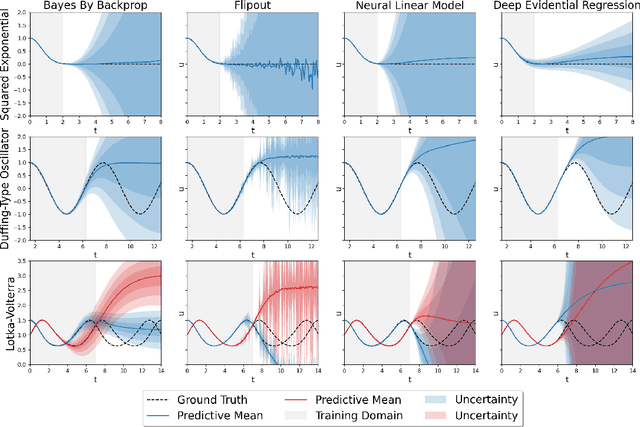
Uncertainty quantification (UQ) helps to make trustworthy predictions based on collected observations and uncertain domain knowledge. With increased usage of deep learning in various applications, the need for efficient UQ methods that can make deep models more reliable has increased as well. Among applications that can benefit from effective handling of uncertainty are the deep learning based differential equation (DE) solvers. We adapt several state-of-the-art UQ methods to get the predictive uncertainty for DE solutions and show the results on four different DE types.