Implicit Regularization Towards Rank Minimization in ReLU Networks

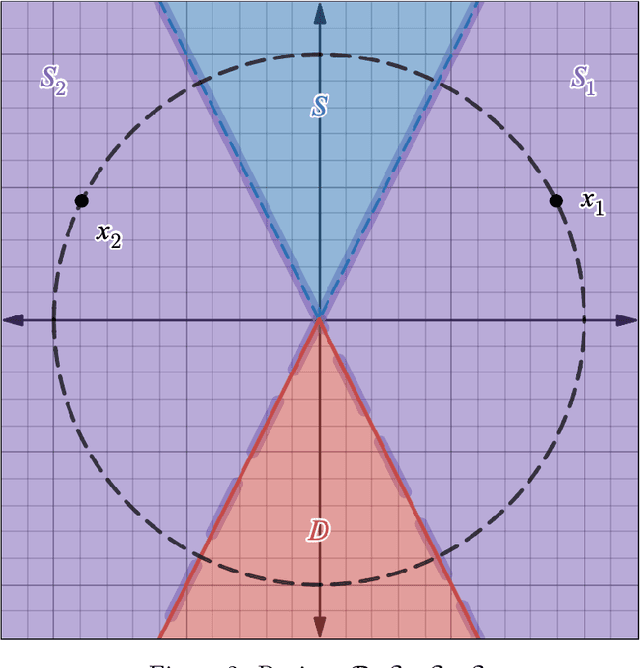
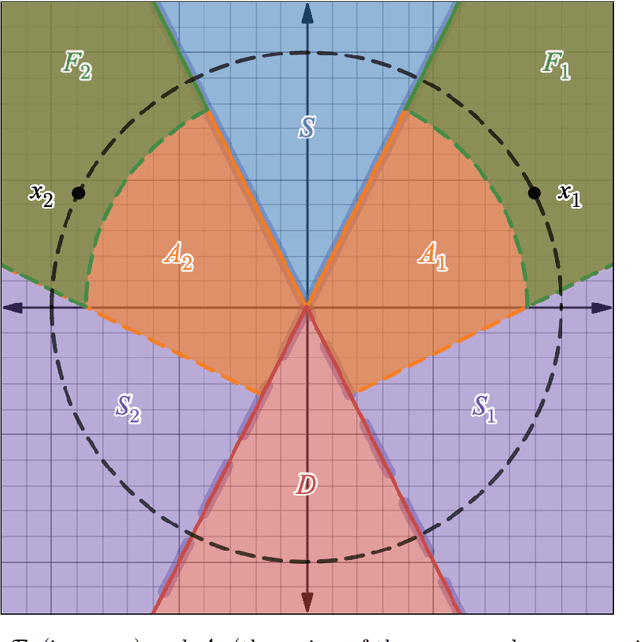
We study the conjectured relationship between the implicit regularization in neural networks, trained with gradient-based methods, and rank minimization of their weight matrices. Previously, it was proved that for linear networks (of depth 2 and vector-valued outputs), gradient flow (GF) w.r.t. the square loss acts as a rank minimization heuristic. However, understanding to what extent this generalizes to nonlinear networks is an open problem. In this paper, we focus on nonlinear ReLU networks, providing several new positive and negative results. On the negative side, we prove (and demonstrate empirically) that, unlike the linear case, GF on ReLU networks may no longer tend to minimize ranks, in a rather strong sense (even approximately, for "most" datasets of size 2). On the positive side, we reveal that ReLU networks of sufficient depth are provably biased towards low-rank solutions in several reasonable settings.

Replay For Safety

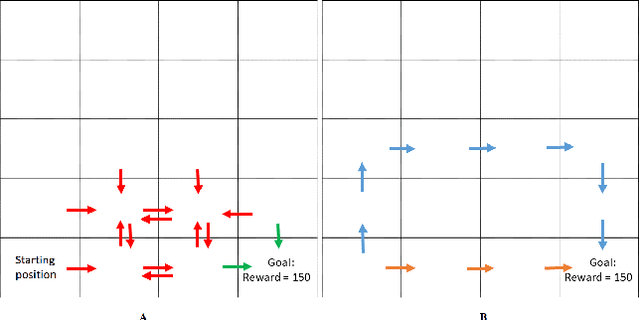
Experience replay \citep{lin1993reinforcement, mnih2015human} is a widely used technique to achieve efficient use of data and improved performance in RL algorithms. In experience replay, past transitions are stored in a memory buffer and re-used during learning. Various suggestions for sampling schemes from the replay buffer have been suggested in previous works, attempting to optimally choose those experiences which will most contribute to the convergence to an optimal policy. Here, we give some conditions on the replay sampling scheme that will ensure convergence, focusing on the well-known Q-learning algorithm in the tabular setting. After establishing sufficient conditions for convergence, we turn to suggest a slightly different usage for experience replay - replaying memories in a biased manner as a means to change the properties of the resulting policy. We initiate a rigorous study of experience replay as a tool to control and modify the properties of the resulting policy. In particular, we show that using an appropriate biased sampling scheme can allow us to achieve a \emph{safe} policy. We believe that using experience replay as a biasing mechanism that allows controlling the resulting policy in desirable ways is an idea with promising potential for many applications.

Convergence Results For Q-Learning With Experience Replay

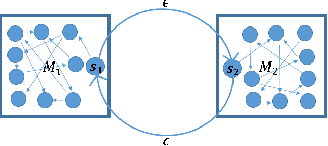
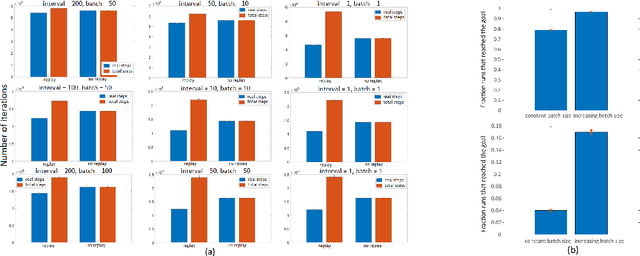
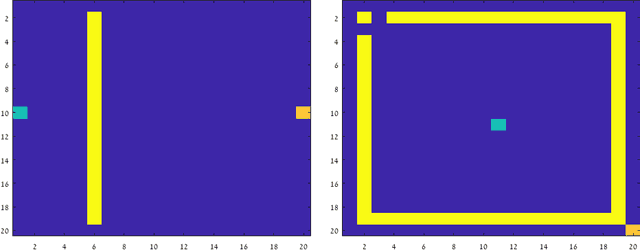
A commonly used heuristic in RL is experience replay (e.g.~\citet{lin1993reinforcement, mnih2015human}), in which a learner stores and re-uses past trajectories as if they were sampled online. In this work, we initiate a rigorous study of this heuristic in the setting of tabular Q-learning. We provide a convergence rate guarantee, and discuss how it compares to the convergence of Q-learning depending on important parameters such as the frequency and number of replay iterations. We also provide theoretical evidence showing when we might expect this heuristic to strictly improve performance, by introducing and analyzing a simple class of MDPs. Finally, we provide some experiments to support our theoretical findings.

A Stochastic Newton Algorithm for Distributed Convex Optimization

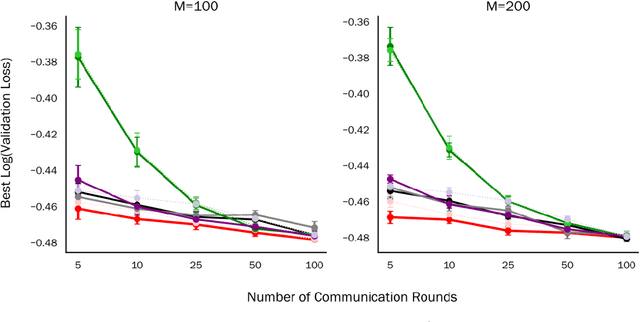
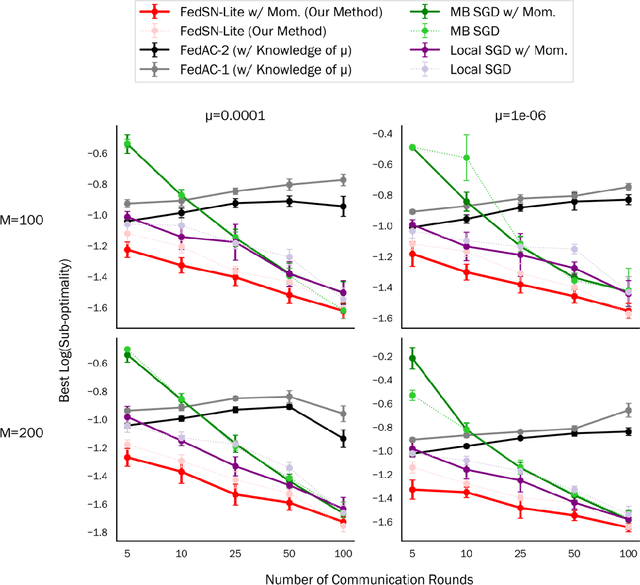
We propose and analyze a stochastic Newton algorithm for homogeneous distributed stochastic convex optimization, where each machine can calculate stochastic gradients of the same population objective, as well as stochastic Hessian-vector products (products of an independent unbiased estimator of the Hessian of the population objective with arbitrary vectors), with many such stochastic computations performed between rounds of communication. We show that our method can reduce the number, and frequency, of required communication rounds compared to existing methods without hurting performance, by proving convergence guarantees for quasi-self-concordant objectives (e.g., logistic regression), alongside empirical evidence.

On Margin Maximization in Linear and ReLU Networks

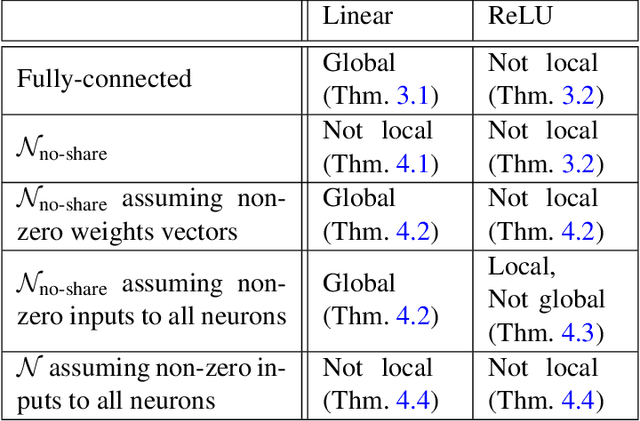
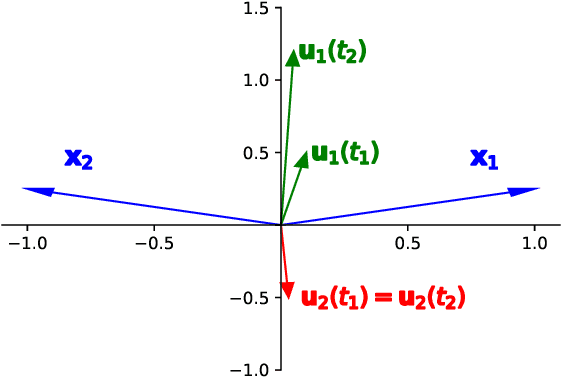
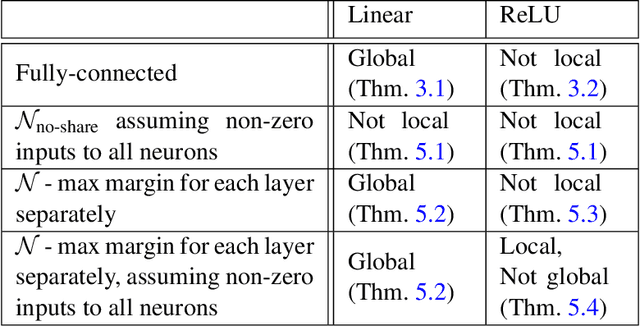
The implicit bias of neural networks has been extensively studied in recent years. Lyu and Li [2019] showed that in homogeneous networks trained with the exponential or the logistic loss, gradient flow converges to a KKT point of the max margin problem in the parameter space. However, that leaves open the question of whether this point will generally be an actual optimum of the max margin problem. In this paper, we study this question in detail, for several neural network architectures involving linear and ReLU activations. Perhaps surprisingly, we show that in many cases, the KKT point is not even a local optimum of the max margin problem. On the flip side, we identify multiple settings where a local or global optimum can be guaranteed. Finally, we answer a question posed in Lyu and Li [2019] by showing that for non-homogeneous networks, the normalized margin may strictly decrease over time.

On the Optimal Memorization Power of ReLU Neural Networks

We study the memorization power of feedforward ReLU neural networks. We show that such networks can memorize any $N$ points that satisfy a mild separability assumption using $\tilde{O}\left(\sqrt{N}\right)$ parameters. Known VC-dimension upper bounds imply that memorizing $N$ samples requires $\Omega(\sqrt{N})$ parameters, and hence our construction is optimal up to logarithmic factors. We also give a generalized construction for networks with depth bounded by $1 \leq L \leq \sqrt{N}$, for memorizing $N$ samples using $\tilde{O}(N/L)$ parameters. This bound is also optimal up to logarithmic factors. Our construction uses weights with large bit complexity. We prove that having such a large bit complexity is both necessary and sufficient for memorization with a sub-linear number of parameters.

Random Shuffling Beats SGD Only After Many Epochs on Ill-Conditioned Problems

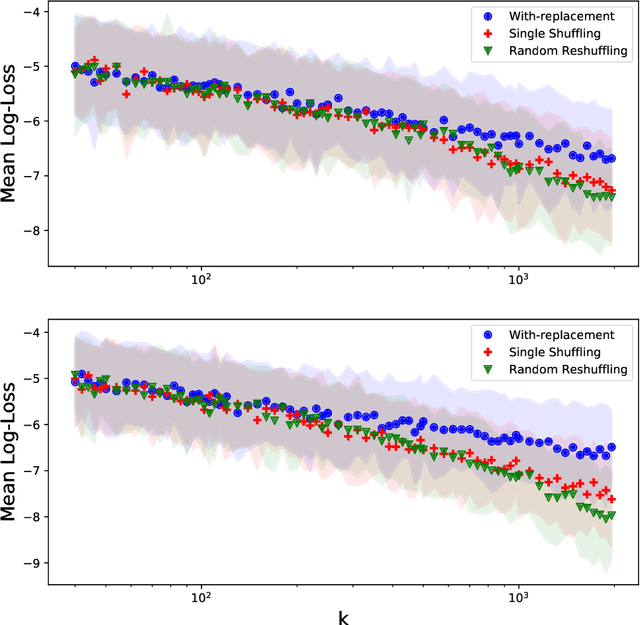
Recently, there has been much interest in studying the convergence rates of without-replacement SGD, and proving that it is faster than with-replacement SGD in the worst case. However, these works ignore or do not provide tight bounds in terms of the problem's geometry, including its condition number. Perhaps surprisingly, we prove that when the condition number is taken into account, without-replacement SGD \emph{does not} significantly improve on with-replacement SGD in terms of worst-case bounds, unless the number of epochs (passes over the data) is larger than the condition number. Since many problems in machine learning and other areas are both ill-conditioned and involve large datasets, this indicates that without-replacement does not necessarily improve over with-replacement sampling for realistic iteration budgets. We show this by providing new lower and upper bounds which are tight (up to log factors), for quadratic problems with commuting quadratic terms, precisely quantifying the dependence on the problem parameters.

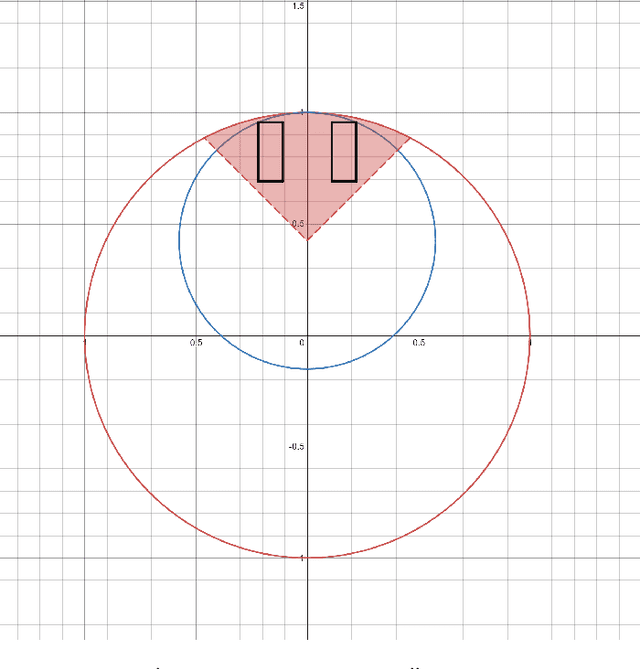
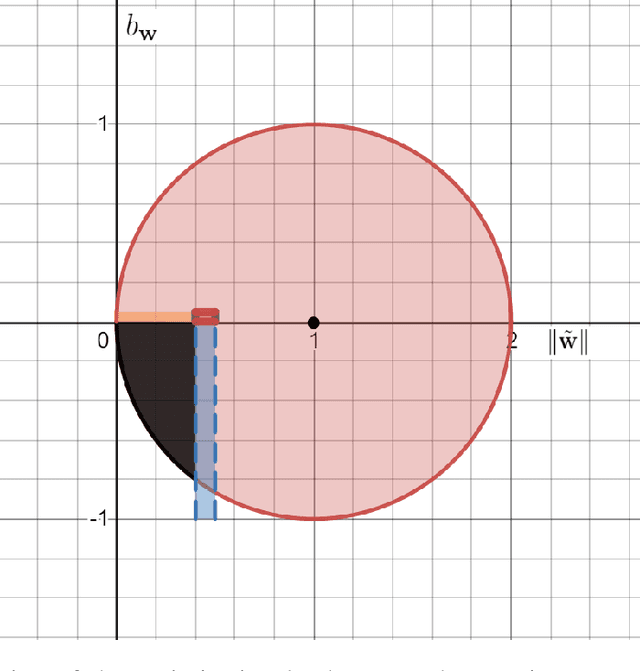
Learning a Single Neuron with Bias Using Gradient Descent

We theoretically study the fundamental problem of learning a single neuron with a bias term ($\mathbf{x} \mapsto \sigma(<\mathbf{w},\mathbf{x}> + b)$) in the realizable setting with the ReLU activation, using gradient descent. Perhaps surprisingly, we show that this is a significantly different and more challenging problem than the bias-less case (which was the focus of previous works on single neurons), both in terms of the optimization geometry as well as the ability of gradient methods to succeed in some scenarios. We provide a detailed study of this problem, characterizing the critical points of the objective, demonstrating failure cases, and providing positive convergence guarantees under different sets of assumptions. To prove our results, we develop some tools which may be of independent interest, and improve previous results on learning single neurons.

Oracle Complexity in Nonsmooth Nonconvex Optimization

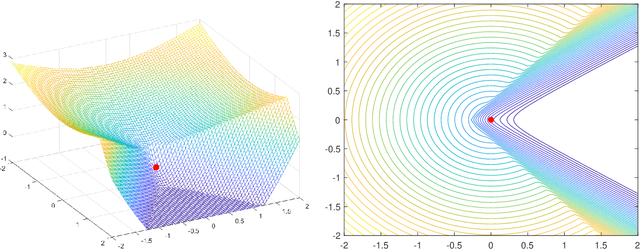
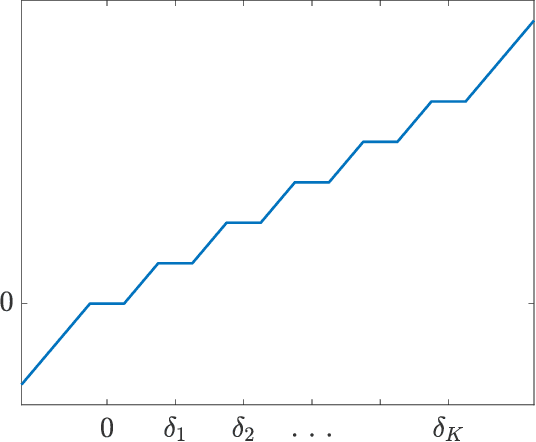
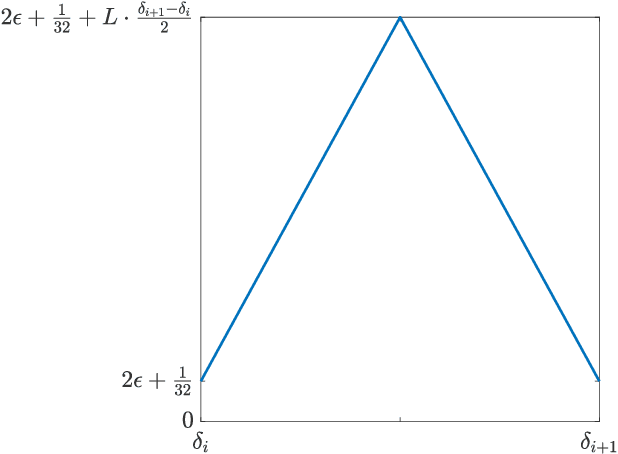
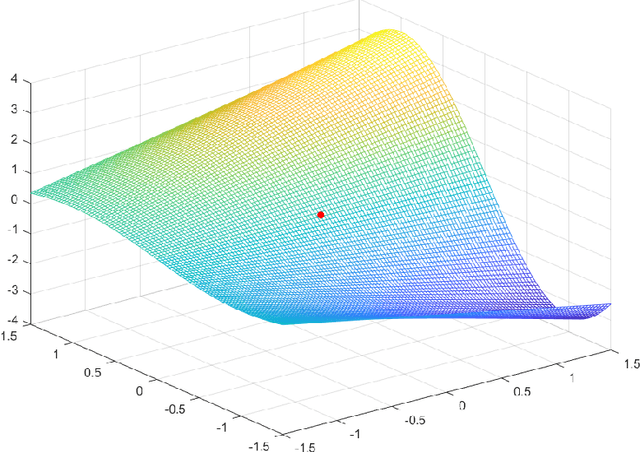
It is well-known that given a smooth, bounded-from-below, and possibly nonconvex function, standard gradient-based methods can find $\epsilon$-stationary points (with gradient norm less than $\epsilon$) in $\mathcal{O}(1/\epsilon^2)$ iterations. However, many important nonconvex optimization problems, such as those associated with training modern neural networks, are inherently not smooth, making these results inapplicable. In this paper, we study nonsmooth nonconvex optimization from an oracle complexity viewpoint, where the algorithm is assumed to be given access only to local information about the function at various points. We provide two main results (under mild assumptions): First, we consider the problem of getting near $\epsilon$-stationary points. This is perhaps the most natural relaxation of finding $\epsilon$-stationary points, which is impossible in the nonsmooth nonconvex case. We prove that this relaxed goal cannot be achieved efficiently, for any distance and $\epsilon$ smaller than some constants. Our second result deals with the possibility of tackling nonsmooth nonconvex optimization by reduction to smooth optimization: Namely, applying smooth optimization methods on a smooth approximation of the objective function. For this approach, we prove an inherent trade-off between oracle complexity and smoothness: On the one hand, smoothing a nonsmooth nonconvex function can be done very efficiently (e.g., by randomized smoothing), but with dimension-dependent factors in the smoothness parameter, which can strongly affect iteration complexity when plugging into standard smooth optimization methods. On the other hand, these dimension factors can be eliminated with suitable smoothing methods, but only by making the oracle complexity of the smoothing process exponentially large.

Size and Depth Separation in Approximating Natural Functions with Neural Networks

When studying the expressive power of neural networks, a main challenge is to understand how the size and depth of the network affect its ability to approximate real functions. However, not all functions are interesting from a practical viewpoint: functions of interest usually have a polynomially-bounded Lipschitz constant, and can be computed efficiently. We call functions that satisfy these conditions "natural", and explore the benefits of size and depth for approximation of natural functions with ReLU networks. As we show, this problem is more challenging than the corresponding problem for non-natural functions. We give barriers to showing depth-lower-bounds: Proving existence of a natural function that cannot be approximated by polynomial-size networks of depth $4$ would settle longstanding open problems in computational complexity. It implies that beyond depth $4$ there is a barrier to showing depth-separation for natural functions, even between networks of constant depth and networks of nonconstant depth. We also study size-separation, namely, whether there are natural functions that can be approximated with networks of size $O(s(d))$, but not with networks of size $O(s'(d))$. We show a complexity-theoretic barrier to proving such results beyond size $O(d\log^2(d))$, but also show an explicit natural function, that can be approximated with networks of size $O(d)$ and not with networks of size $o(d/\log d)$. For approximation in $L_\infty$ we achieve such separation already between size $O(d)$ and size $o(d)$. Moreover, we show superpolynomial size lower bounds and barriers to such lower bounds, depending on the assumptions on the function. Our size-separation results rely on an analysis of size lower bounds for Boolean functions, which is of independent interest: We show linear size lower bounds for computing explicit Boolean functions with neural networks and threshold circuits.