TowerDebias: A Novel Debiasing Method based on the Tower Property

Decision-making processes have increasingly come to rely on sophisticated machine learning tools, raising concerns about the fairness of their predictions with respect to any sensitive groups. The widespread use of commercial black-box machine learning models necessitates careful consideration of their legal and ethical implications on consumers. In situations where users have access to these "black-box" models, a key question emerges: how can we mitigate or eliminate the influence of sensitive attributes, such as race or gender? We propose towerDebias (tDB), a novel approach designed to reduce the influence of sensitive variables in predictions made by black-box models. Using the Tower Property from probability theory, tDB aims to improve prediction fairness during the post-processing stage in a manner amenable to the Fairness-Utility Tradeoff. This method is highly flexible, requiring no prior knowledge of the original model's internal structure, and can be extended to a range of different applications. We provide a formal improvement theorem for tDB and demonstrate its effectiveness in both regression and classification tasks, underscoring its impact on the fairness-utility tradeoff.

dsld: A Socially Relevant Tool for Teaching Statistics

The growing power of data science can play a crucial role in addressing social discrimination, necessitating nuanced understanding and effective mitigation strategies of potential biases. Data Science Looks At Discrimination (dsld) is an R and Python package designed to provide users with a comprehensive toolkit of statistical and graphical methods for assessing possible discrimination related to protected groups, such as race, gender, and age. Our software offers techniques for discrimination analysis by identifying and mitigating confounding variables, along with methods for reducing bias in predictive models. In educational settings, dsld offers instructors powerful tools to teach important statistical principles through motivating real world examples of discrimination analysis. The inclusion of an 80-page Quarto book further supports users, from statistics educators to legal professionals, in effectively applying these analytical tools to real world scenarios.

Walk a Mile in Their Shoes: a New Fairness Criterion for Machine Learning

The old empathetic adage, ``Walk a mile in their shoes,'' asks that one imagine the difficulties others may face. This suggests a new ML counterfactual fairness criterion, based on a \textit{group} level: How would members of a nonprotected group fare if their group were subject to conditions in some protected group? Instead of asking what sentence would a particular Caucasian convict receive if he were Black, take that notion to entire groups; e.g. how would the average sentence for all White convicts change if they were Black, but with their same White characteristics, e.g. same number of prior convictions? We frame the problem and study it empirically, for different datasets. Our approach also is a solution to the problem of covariate correlation with sensitive attributes.

A Novel Regularization Approach to Fair ML

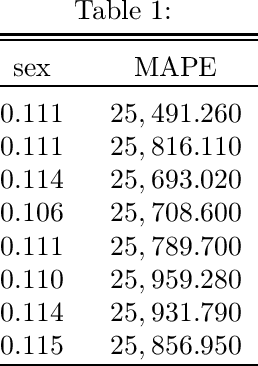
A number of methods have been introduced for the fair ML issue, most of them complex and many of them very specific to the underlying ML moethodology. Here we introduce a new approach that is simple, easily explained, and potentially applicable to a number of standard ML algorithms. Explicitly Deweighted Features (EDF) reduces the impact of each feature among the proxies of sensitive variables, allowing a different amount of deweighting applied to each such feature. The user specifies the deweighting hyperparameters, to achieve a given point in the Utility/Fairness tradeoff spectrum. We also introduce a new, simple criterion for evaluating the degree of protection afforded by any fair ML method.

Polynomial Regression As an Alternative to Neural Nets

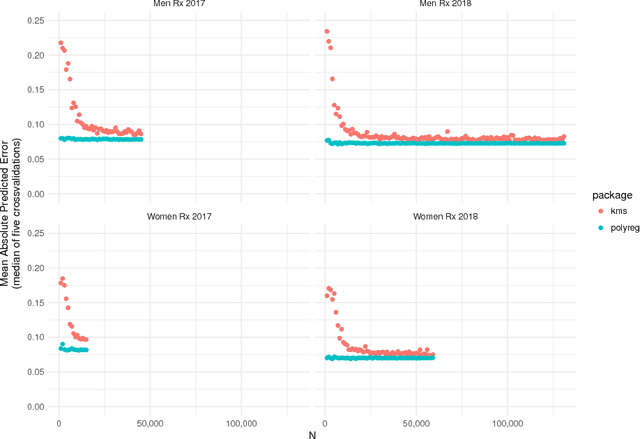
Despite the success of neural networks (NNs), there is still a concern among many over their "black box" nature. Why do they work? Here we present a simple analytic argument that NNs are in fact essentially polynomial regression models. This view will have various implications for NNs, e.g. providing an explanation for why convergence problems arise in NNs, and it gives rough guidance on avoiding overfitting. In addition, we use this phenomenon to predict and confirm a multicollinearity property of NNs not previously reported in the literature. Most importantly, given this loose correspondence, one may choose to routinely use polynomial models instead of NNs, thus avoiding some major problems of the latter, such as having to set many tuning parameters and dealing with convergence issues. We present a number of empirical results; in each case, the accuracy of the polynomial approach matches or exceeds that of NN approaches. A many-featured, open-source software package, polyreg, is available.

Improved Estimation of Class Prior Probabilities through Unlabeled Data

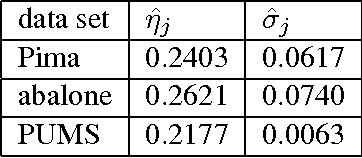
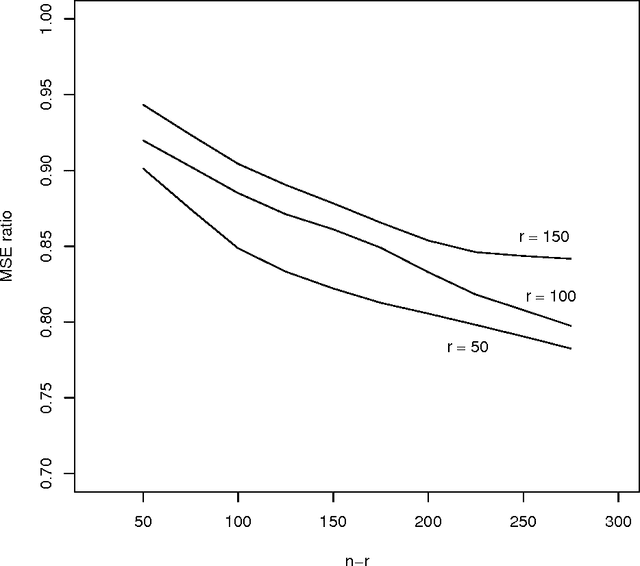
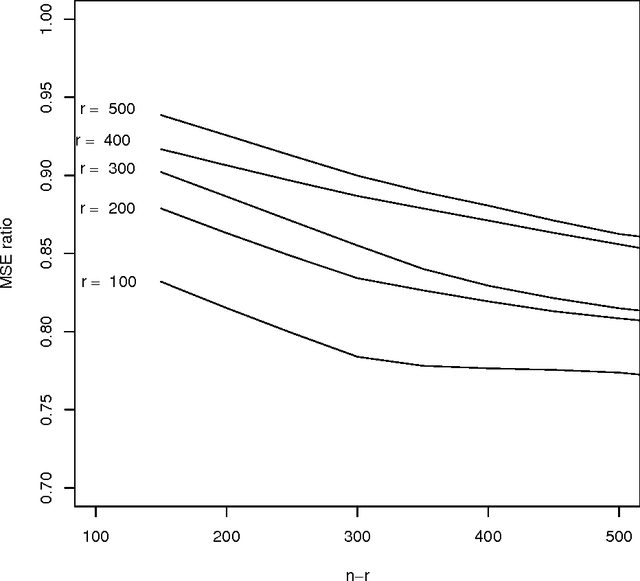
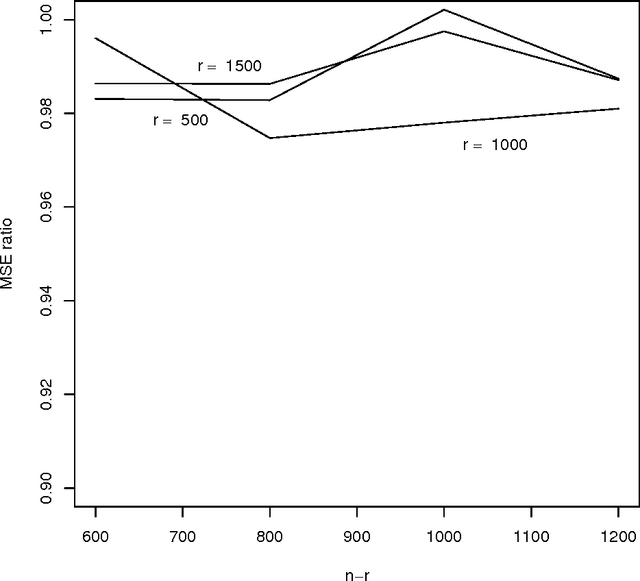
Work in the classification literature has shown that in computing a classification function, one need not know the class membership of all observations in the training set; the unlabeled observations still provide information on the marginal distribution of the feature set, and can thus contribute to increased classification accuracy for future observations. The present paper will show that this scheme can also be used for the estimation of class prior probabilities, which would be very useful in applications in which it is difficult or expensive to determine class membership. Both parametric and nonparametric estimators are developed. Asymptotic distributions of the estimators are derived, and it is proven that the use of the unlabeled observations does reduce asymptotic variance. This methodology is also extended to the estimation of subclass probabilities.