A scalable and real-time neural decoder for topological quantum codes

Fault-tolerant quantum computing will require error rates far below those achievable with physical qubits. Quantum error correction (QEC) bridges this gap, but depends on decoders being simultaneously fast, accurate, and scalable. This combination of requirements has not yet been met by a machine-learning decoder, nor by any decoder for promising resource-efficient codes such as the colour code. Here we introduce AlphaQubit 2, a neural-network decoder that achieves near-optimal logical error rates for both surface and colour codes at large scales under realistic noise. For the colour code, it is orders of magnitude faster than other high-accuracy decoders. For the surface code, we demonstrate real-time decoding faster than 1 microsecond per cycle up to distance 11 on current commercial accelerators with better accuracy than leading real-time decoders. These results support the practical application of a wider class of promising QEC codes, and establish a credible path towards high-accuracy, real-time neural decoding at the scales required for fault-tolerant quantum computation.

Learning Irreducible Representations of Noncommutative Lie Groups

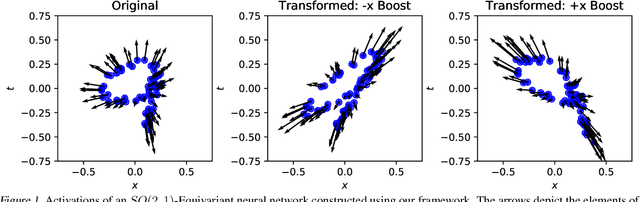
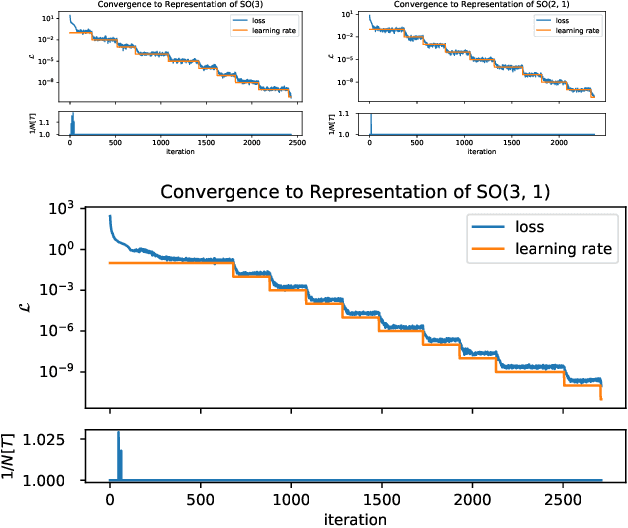
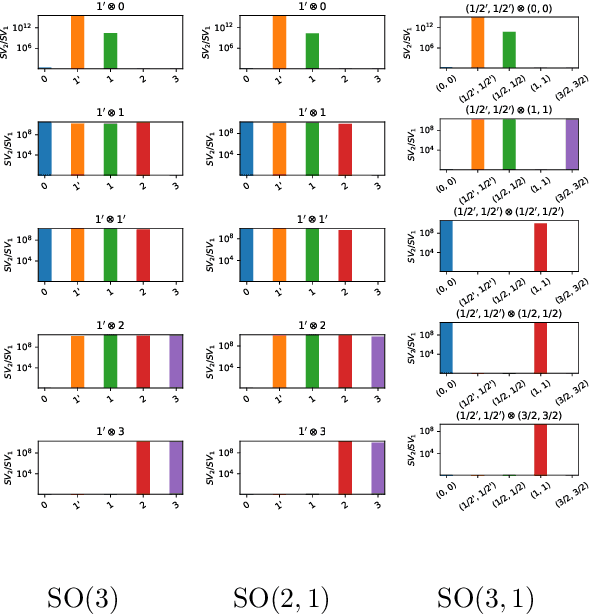
Recent work has made exciting theoretical and practical progress towards neural networks that are equivariant to symmetries such as rotations. However, current techniques require explicit group representations, which generally limits us to those groups with analytically derived matrix formulas. In this work, we present a numerical technique for finding irreducible representations of noncommutative Lie groups. We demonstrate that the structure of the Lie algebras associated with these groups can be used to learn explicit representation matrices to high precision. This provides an automated program to build neural networks that are equivariant to a much wider class of transformations, including previously intractable cases such as the Poincar\'e group (rotations, translations, and boosts).