Evaluating Robustness to Dataset Shift via Parametric Robustness Sets

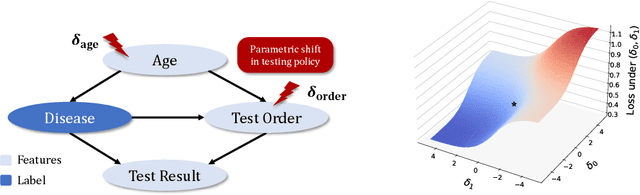
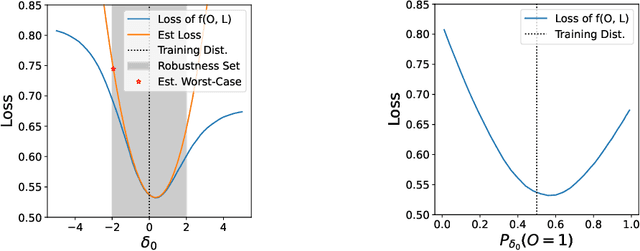
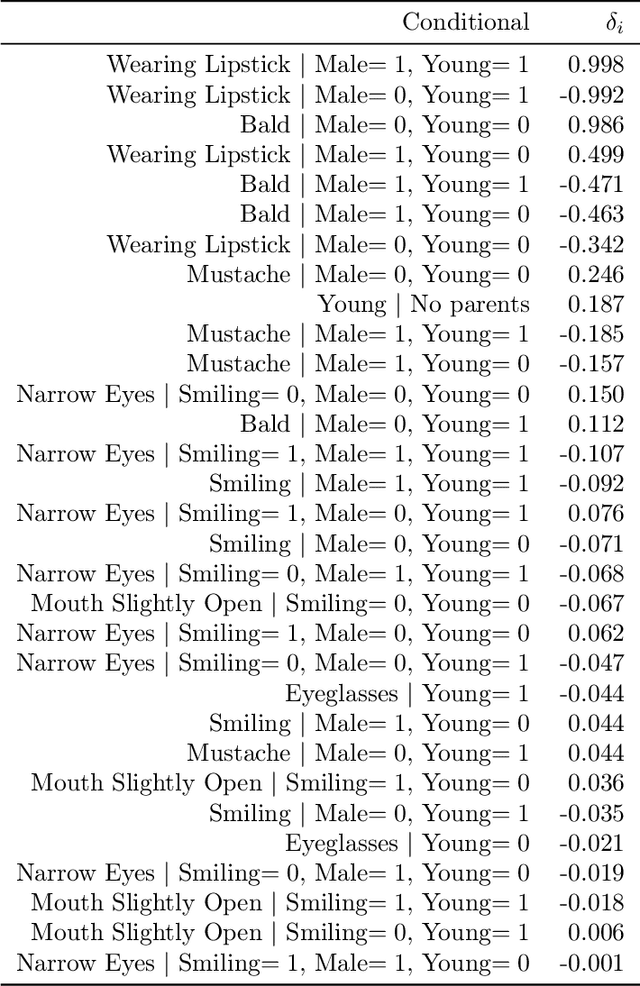
We give a method for proactively identifying small, plausible shifts in distribution which lead to large differences in model performance. To ensure that these shifts are plausible, we parameterize them in terms of interpretable changes in causal mechanisms of observed variables. This defines a parametric robustness set of plausible distributions and a corresponding worst-case loss. While the loss under an individual parametric shift can be estimated via reweighting techniques such as importance sampling, the resulting worst-case optimization problem is non-convex, and the estimate may suffer from large variance. For small shifts, however, we can construct a local second-order approximation to the loss under shift and cast the problem of finding a worst-case shift as a particular non-convex quadratic optimization problem, for which efficient algorithms are available. We demonstrate that this second-order approximation can be estimated directly for shifts in conditional exponential family models, and we bound the approximation error. We apply our approach to a computer vision task (classifying gender from images), revealing sensitivity to shifts in non-causal attributes.

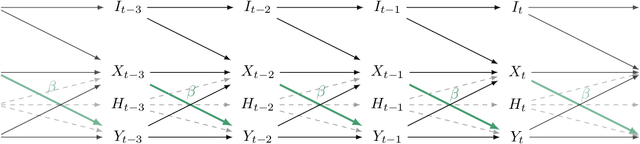
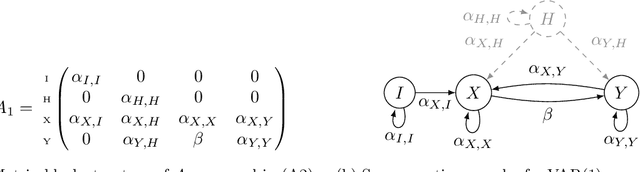
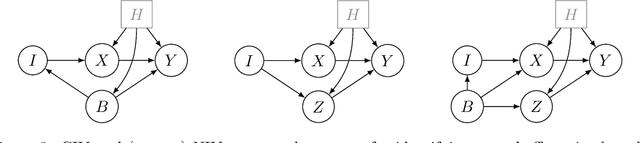
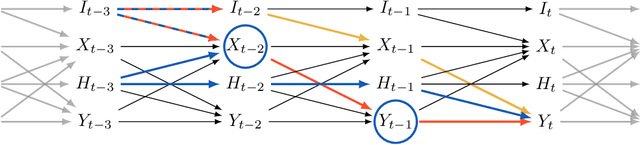
Identifying Causal Effects using Instrumental Time Series: Nuisance IV and Correcting for the Past

Instrumental variable (IV) regression relies on instruments to infer causal effects from observational data with unobserved confounding. We consider IV regression in time series models, such as vector auto-regressive (VAR) processes. Direct applications of i.i.d. techniques are generally inconsistent as they do not correctly adjust for dependencies in the past. In this paper, we propose methodology for constructing identifying equations that can be used for consistently estimating causal effects. To do so, we develop nuisance IV, which can be of interest even in the i.i.d. case, as it generalizes existing IV methods. We further propose a graph marginalization framework that allows us to apply nuisance and other IV methods in a principled way to time series. Our framework builds on the global Markov property, which we prove holds for VAR processes. For VAR(1) processes, we prove identifiability conditions that relate to Jordan forms and are different from the well-known rank conditions in the i.i.d. case (they do not require as many instruments as covariates, for example). We provide methods, prove their consistency, and show how the inferred causal effect can be used for distribution generalization. Simulation experiments corroborate our theoretical results. We provide ready-to-use Python code.

Invariant Ancestry Search

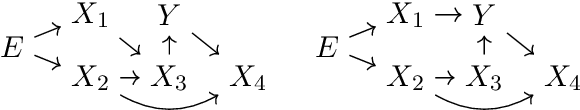
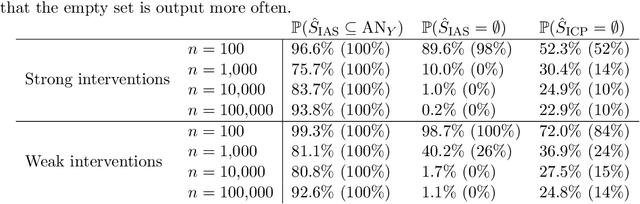
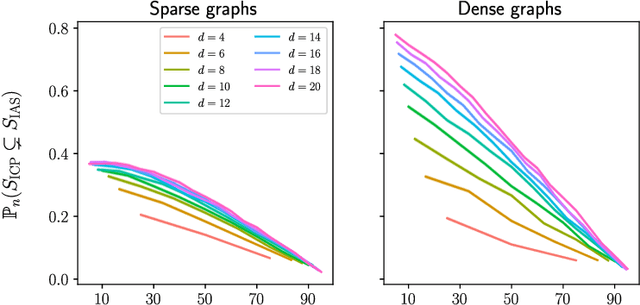
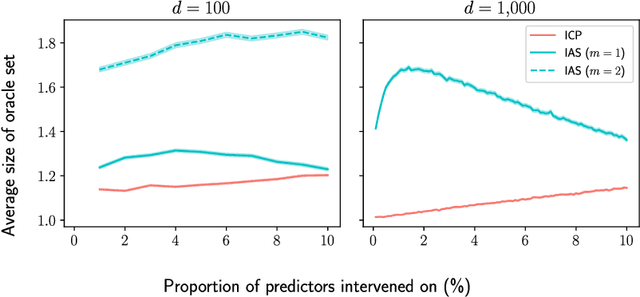
Recently, methods have been proposed that exploit the invariance of prediction models with respect to changing environments to infer subsets of the causal parents of a response variable. If the environments influence only few of the underlying mechanisms, the subset identified by invariant causal prediction, for example, may be small, or even empty. We introduce the concept of minimal invariance and propose invariant ancestry search (IAS). In its population version, IAS outputs a set which contains only ancestors of the response and is a superset of the output of ICP. When applied to data, corresponding guarantees hold asymptotically if the underlying test for invariance has asymptotic level and power. We develop scalable algorithms and perform experiments on simulated and real data.

Local Independence Testing for Point Processes

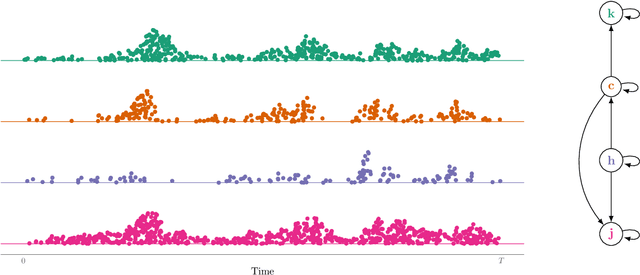
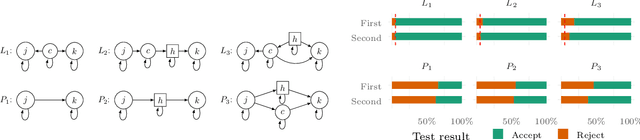
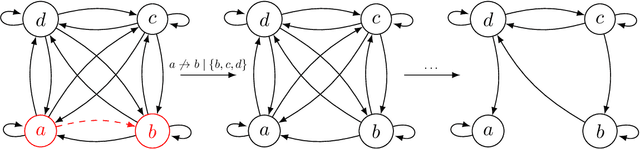
Constraint based causal structure learning for point processes require empirical tests of local independence. Existing tests require strong model assumptions, e.g. that the true data generating model is a Hawkes process with no latent confounders. Even when restricting attention to Hawkes processes, latent confounders are a major technical difficulty because a marginalized process will generally not be a Hawkes process itself. We introduce an expansion similar to Volterra expansions as a tool to represent marginalized intensities. Our main theoretical result is that such expansions can approximate the true marginalized intensity arbitrarily well. Based on this we propose a test of local independence and investigate its properties in real and simulated data.

Invariant Policy Learning: A Causal Perspective

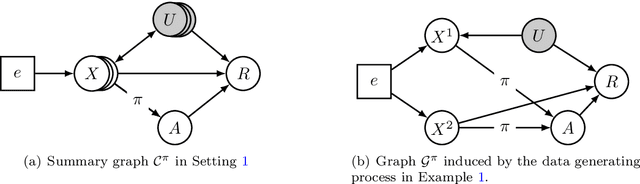
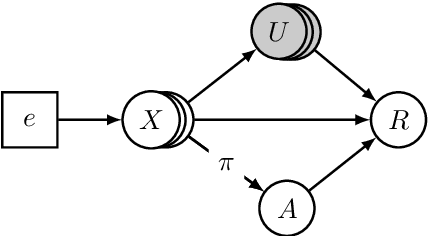
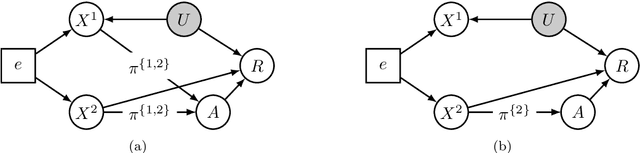
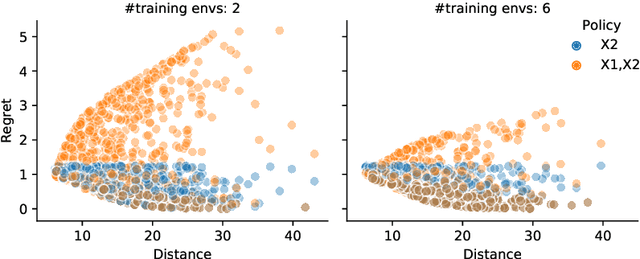
In the past decade, contextual bandit and reinforcement learning algorithms have been successfully used in various interactive learning systems such as online advertising, recommender systems, and dynamic pricing. However, they have yet to be widely adopted in high-stakes application domains, such as healthcare. One reason may be that existing approaches assume that the underlying mechanisms are static in the sense that they do not change over time or over different environments. In many real world systems, however, the mechanisms are subject to shifts across environments which may invalidate the static environment assumption. In this paper, we tackle the problem of environmental shifts under the framework of offline contextual bandits. We view the environmental shift problem through the lens of causality and propose multi-environment contextual bandits that allow for changes in the underlying mechanisms. We adopt the concept of invariance from the causality literature and introduce the notion of policy invariance. We argue that policy invariance is only relevant if unobserved confounders are present and show that, in that case, an optimal invariant policy is guaranteed, under certain assumptions, to generalize across environments. Our results do not only provide a solution to the environmental shift problem but also establish concrete connections among causality, invariance and contextual bandits.

Regularizing towards Causal Invariance: Linear Models with Proxies

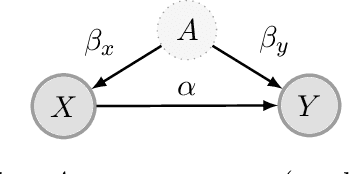
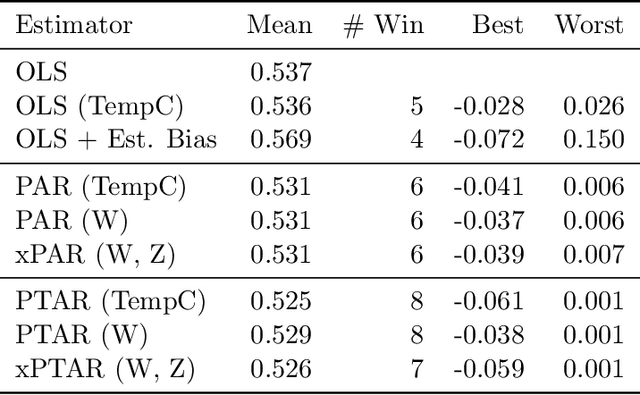
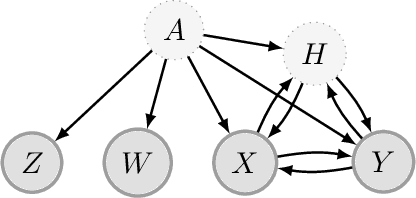
We propose a method for learning linear models whose predictive performance is robust to causal interventions on unobserved variables, when noisy proxies of those variables are available. Our approach takes the form of a regularization term that trades off between in-distribution performance and robustness to interventions. Under the assumption of a linear structural causal model, we show that a single proxy can be used to create estimators that are prediction optimal under interventions of bounded strength. This strength depends on the magnitude of the measurement noise in the proxy, which is, in general, not identifiable. In the case of two proxy variables, we propose a modified estimator that is prediction optimal under interventions up to a known strength. We further show how to extend these estimators to scenarios where additional information about the "test time" intervention is available during training. We evaluate our theoretical findings in synthetic experiments and using real data of hourly pollution levels across several cities in China.

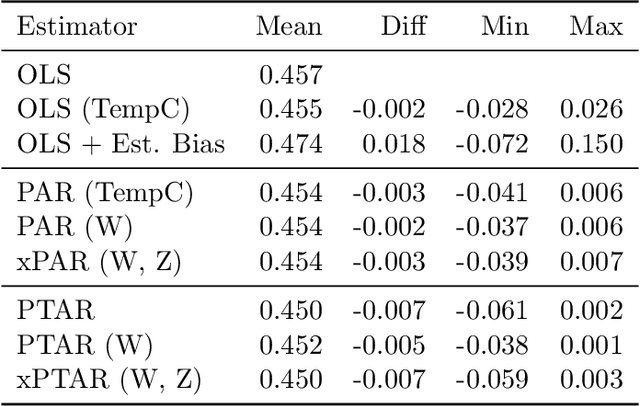
Causal structure learning from time series: Large regression coefficients may predict causal links better in practice than small p-values

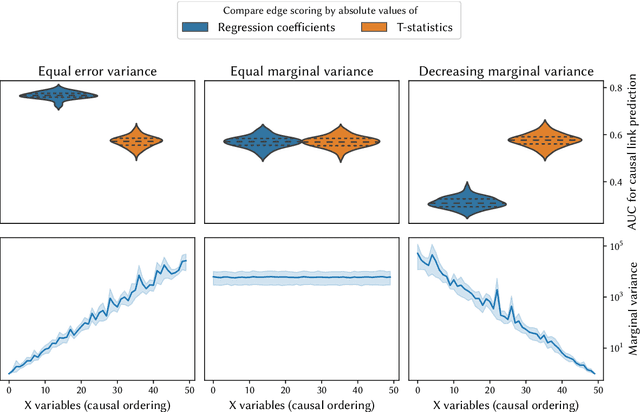
In this article, we describe the algorithms for causal structure learning from time series data that won the Causality 4 Climate competition at the Conference on Neural Information Processing Systems 2019 (NeurIPS). We examine how our combination of established ideas achieves competitive performance on semi-realistic and realistic time series data exhibiting common challenges in real-world Earth sciences data. In particular, we discuss a) a rationale for leveraging linear methods to identify causal links in non-linear systems, b) a simulation-backed explanation as to why large regression coefficients may predict causal links better in practice than small p-values and thus why normalising the data may sometimes hinder causal structure learning. For benchmark usage, we provide implementations at https://github.com/sweichwald/tidybench and detail the algorithms here. We propose the presented competition-proven methods for baseline benchmark comparisons to guide the development of novel algorithms for structure learning from time series.