Factor analysis of dynamic PET images: beyond Gaussian noise

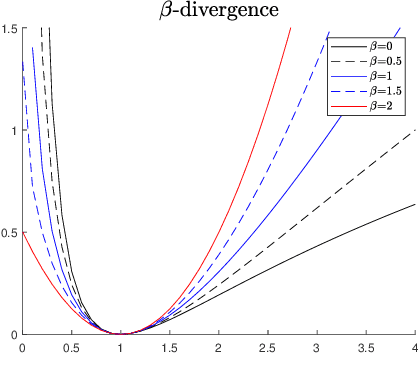
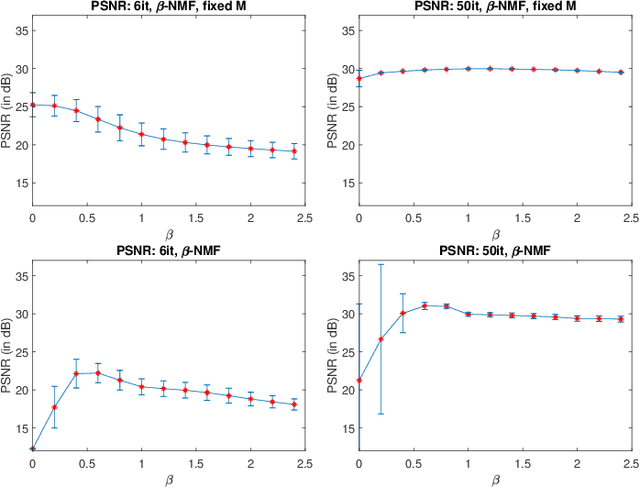
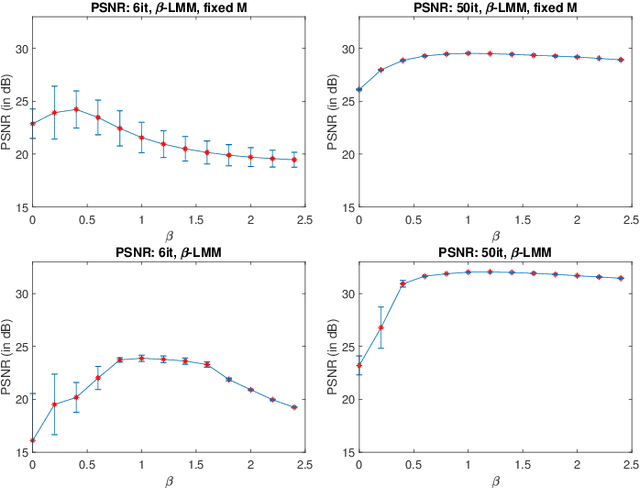
Factor analysis has proven to be a relevant tool for extracting tissue time-activity curves (TACs) in dynamic PET images, since it allows for an unsupervised analysis of the data. To provide reliable and interpretable outputs, it requires to be conducted with respect to a suitable noise statistics. However, the noise in reconstructed dynamic PET images is very difficult to characterize, despite the Poissonian nature of the count-rates. Rather than explicitly modeling the noise distribution, this work proposes to study the relevance of several divergence measures to be used within a factor analysis framework. To this end, the $\beta$-divergence, widely used in other applicative domains, is considered to design the data-fitting term involved in three different factor models. The performances of the resulting algorithms are evaluated for different values of $\beta$, in a range covering Gaussian, Poissonian and Gamma-distributed noises. The results obtained on two different types of synthetic images and one real image show the interest of applying non-standard values of $\beta$ to improve factor analysis.

Coupled dictionary learning for unsupervised change detection between multi-sensor remote sensing images

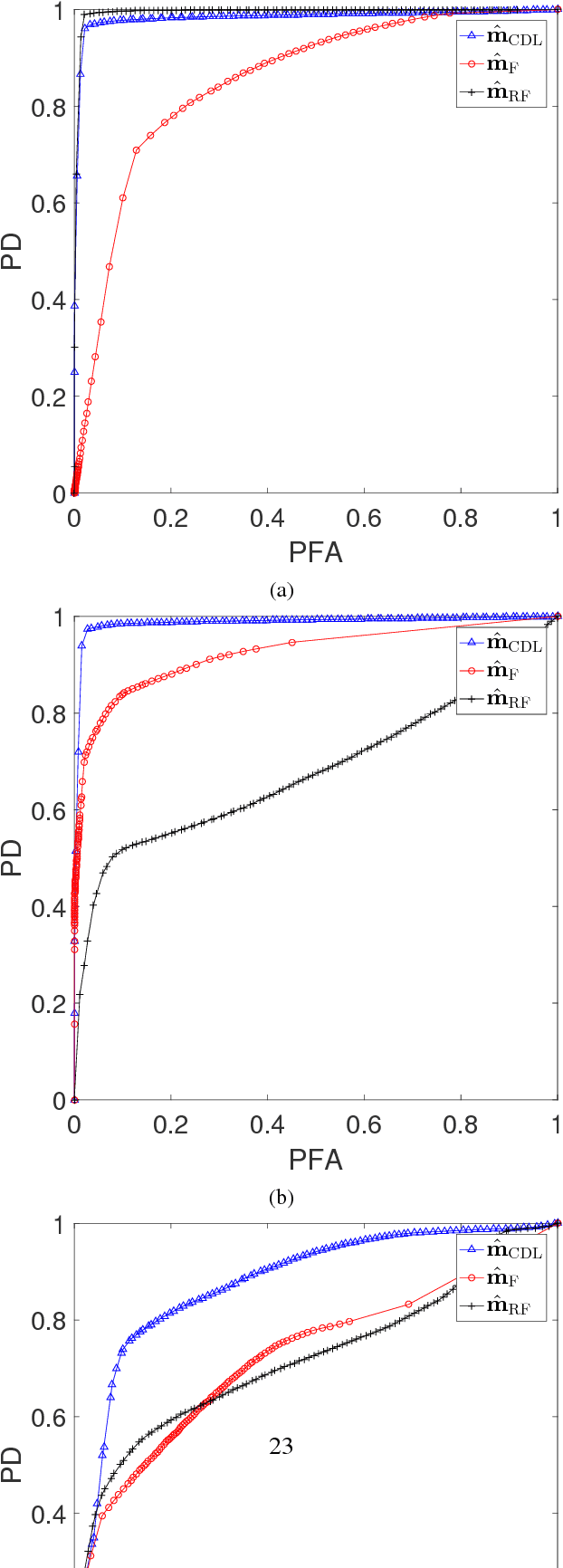
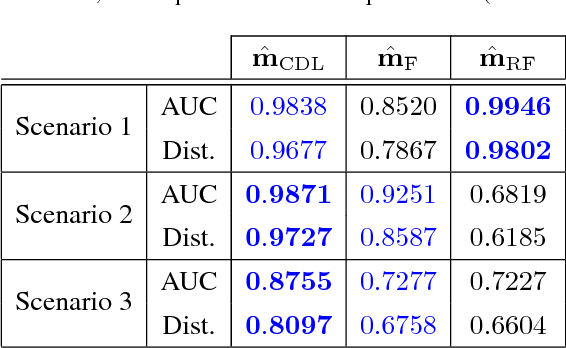
Archetypal scenarios for change detection generally consider two images acquired through sensors of the same modality. However, in some specific cases such as emergency situations, the only images available may be those acquired through sensors with different characteristics. This paper addresses the problem of unsupervisedly detecting changes between two observed images acquired by different sensors. These sensor dissimilarities introduce additional issues in the context of operational change detection that are not addressed by most of classical methods. This paper introduces a novel framework to effectively exploit the available information by modeling the two observed images as a sparse linear combination of atoms belonging to an overcomplete pair of coupled dictionaries learnt from each observed image. As they cover the same geographical location, codes are expected to be globally similar except for possible changes in sparse spatial locations. Thus, the change detection task is envisioned through a dual code estimation which enforces spatial sparsity in the difference between the estimated codes associated with each image. This problem is formulated as an inverse problem which is iteratively solved using an efficient proximal alternating minimization algorithm accounting for nonsmooth and nonconvex functions. The proposed method is applied to real multisensor images with simulated yet realistic and real images. A comparison with state-of-the-art change detection methods evidences the accuracy of the proposed strategy.

Hyperspectral unmixing with spectral variability using adaptive bundles and double sparsity

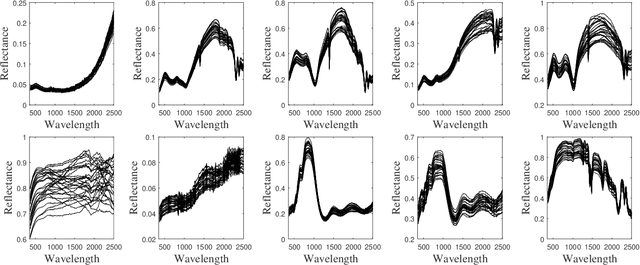
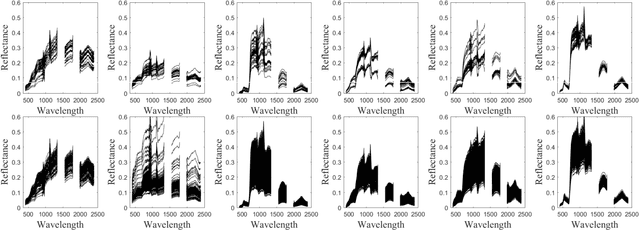
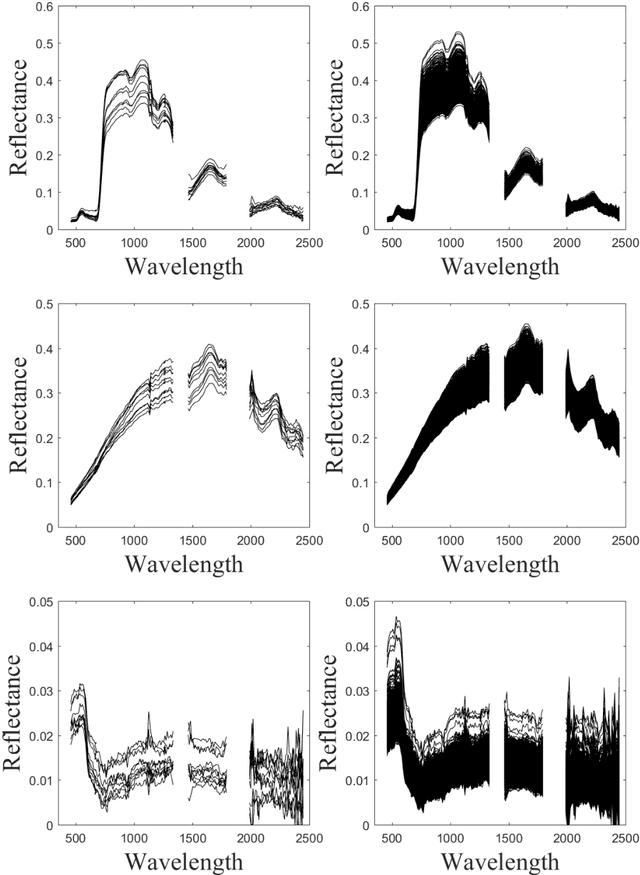
Spectral variability is one of the major issue when conducting hyperspectral unmixing. Within a given image composed of some elementary materials (herein referred to as endmember classes), the spectral signature characterizing these classes may spatially vary due to intrinsic component fluctuations or external factors (illumination). These redundant multiple endmember spectra within each class adversely affect the performance of unmixing methods. This paper proposes a mixing model that explicitly incorporates a hierarchical structure of redundant multiple spectra representing each class. The proposed method is designed to promote sparsity on the selection of both spectra and classes within each pixel. The resulting unmixing algorithm is able to adaptively recover several bundles of endmember spectra associated with each class and robustly estimate abundances. In addition, its flexibility allows a variable number of classes to be present within each pixel of the hyperspectral image to be unmixed. The proposed method is compared with other state-of-the-art unmixing methods that incorporate sparsity using both simulated and real hyperspectral data. The results show that the proposed method can successfully determine the variable number of classes present within each class and estimate the corresponding class abundances.

Robust fusion algorithms for unsupervised change detection between multi-band optical images - A comprehensive case study

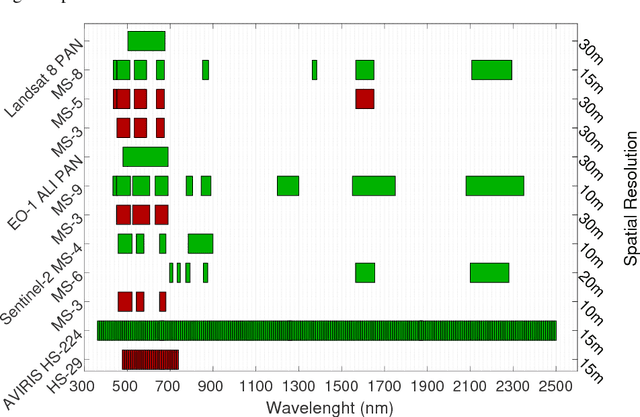
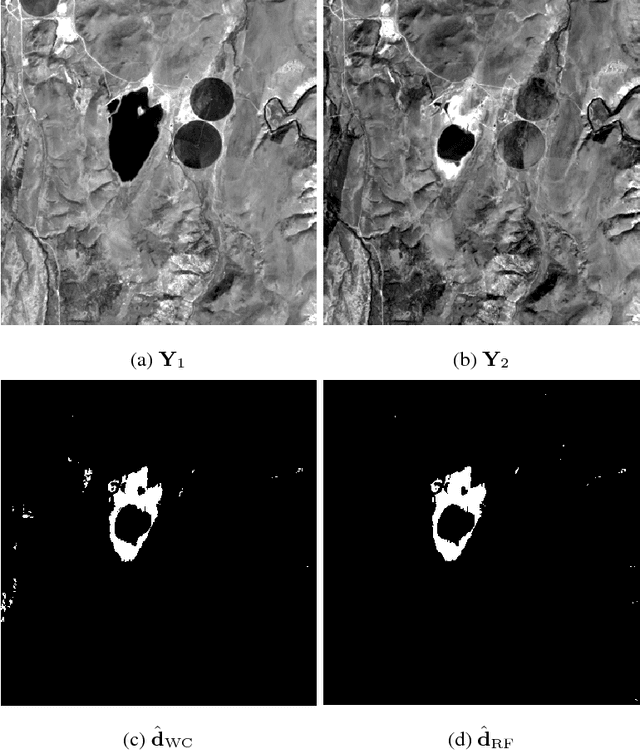
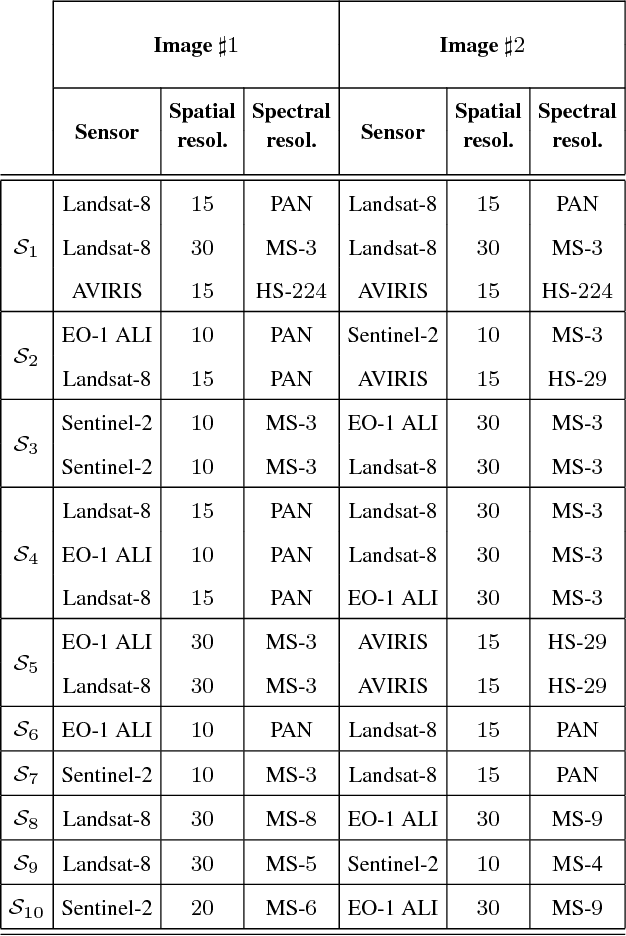
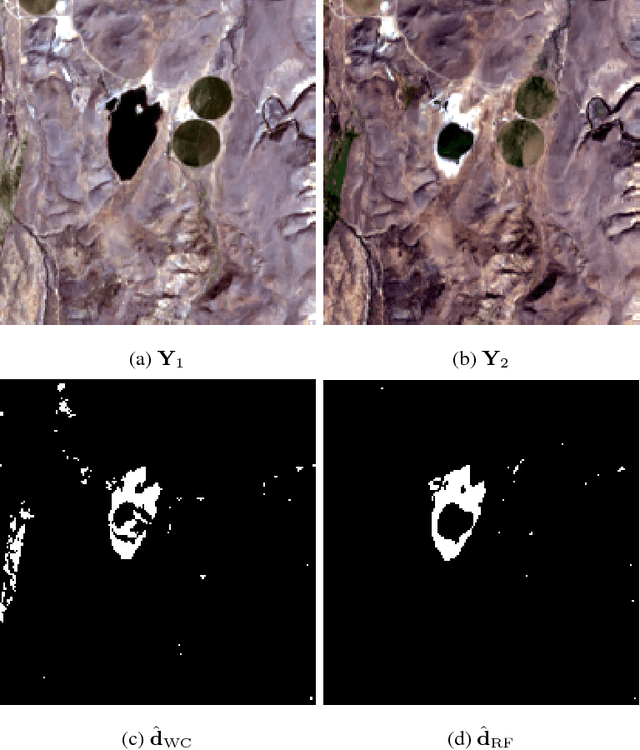
Unsupervised change detection techniques are generally constrained to two multi-band optical images acquired at different times through sensors sharing the same spatial and spectral resolution. This scenario is suitable for a straight comparison of homologous pixels such as pixel-wise differencing. However, in some specific cases such as emergency situations, the only available images may be those acquired through different kinds of sensors with different resolutions. Recently some change detection techniques dealing with images with different spatial and spectral resolutions, have been proposed. Nevertheless, they are focused on a specific scenario where one image has a high spatial and low spectral resolution while the other has a low spatial and high spectral resolution. This paper addresses the problem of detecting changes between any two multi-band optical images disregarding their spatial and spectral resolution disparities. We propose a method that effectively uses the available information by modeling the two observed images as spatially and spectrally degraded versions of two (unobserved) latent images characterized by the same high spatial and high spectral resolutions. Covering the same scene, the latent images are expected to be globally similar except for possible changes in spatially sparse locations. Thus, the change detection task is envisioned through a robust fusion task which enforces the differences between the estimated latent images to be spatially sparse. We show that this robust fusion can be formulated as an inverse problem which is iteratively solved using an alternate minimization strategy. The proposed framework is implemented for an exhaustive list of applicative scenarios and applied to real multi-band optical images. A comparison with state-of-the-art change detection methods evidences the accuracy of the proposed robust fusion-based strategy.

Reconstruction of partially sampled multi-band images - Application to STEM-EELS imaging

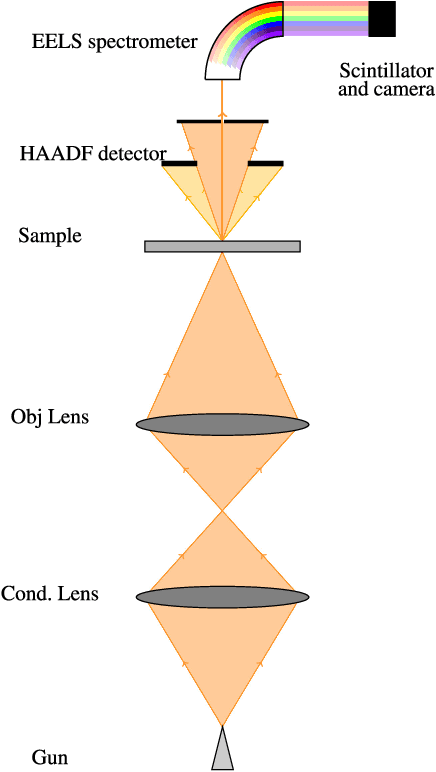
Electron microscopy has shown to be a very powerful tool to map the chemical nature of samples at various scales down to atomic resolution. However, many samples can not be analyzed with an acceptable signal-to-noise ratio because of the radiation damage induced by the electron beam. This is particularly crucial for electron energy loss spectroscopy (EELS) which acquires spectral-spatial data and requires high beam intensity. Since scanning transmission electron microscopes (STEM) are able to acquire data cubes by scanning the electron probe over the sample and recording a spectrum for each spatial position, it is possible to design the scan pattern and to sample only specific pixels. As a consequence, partial acquisition schemes are now conceivable, provided a reconstruction of the full data cube is conducted as a post-processing step. This paper proposes two reconstruction algorithms for multi-band images acquired by STEM-EELS which exploits the spectral structure and the spatial smoothness of the image. The performance of the proposed schemes is illustrated thanks to experiments conducted on a realistic phantom dataset as well as real EELS spectrum-images.

Unmixing dynamic PET images with variable specific binding kinetics

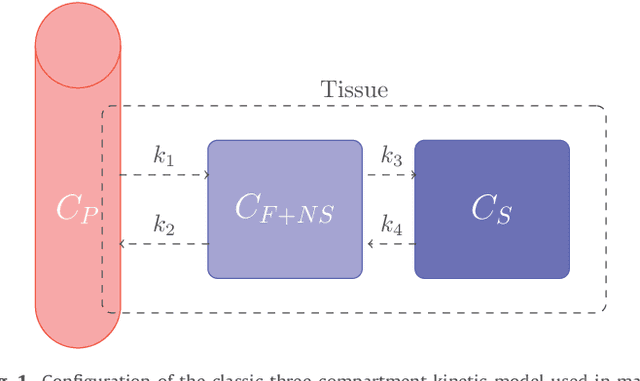
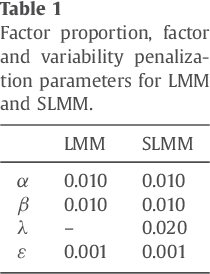
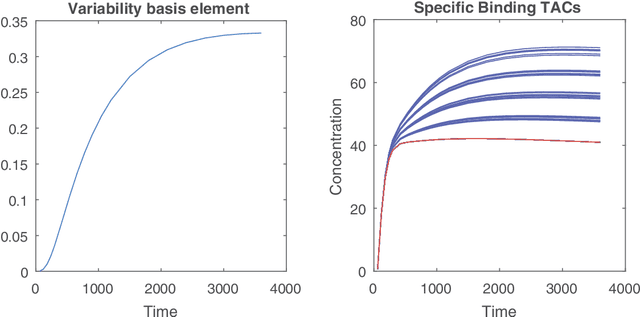
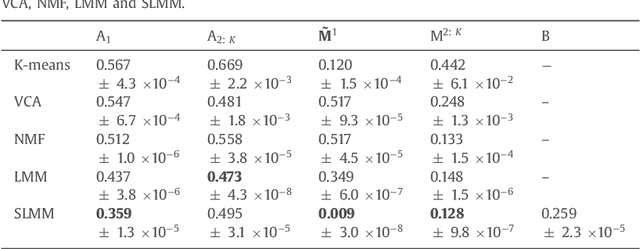
To analyze dynamic positron emission tomography (PET) images, various generic multivariate data analysis techniques have been considered in the literature, such as principal component analysis (PCA), independent component analysis (ICA), factor analysis and nonnegative matrix factorization (NMF). Nevertheless, these conventional approaches neglect any possible nonlinear variations in the time activity curves describing the kinetic behavior of tissues with specific binding, which limits their ability to recover a reliable, understandable and interpretable description of the data. This paper proposes an alternative analysis paradigm that accounts for spatial fluctuations in the exchange rate of the tracer between a free compartment and a specifically bound ligand compartment. The method relies on the concept of linear unmixing, usually applied on the hyperspectral domain, which combines NMF with a sum-to-one constraint that ensures an exhaustive description of the mixtures. The spatial variability of the signature corresponding to the specific binding tissue is explicitly modeled through a perturbed component. The performance of the method is assessed on both synthetic and real data and is shown to compete favorably when compared to other conventional analysis methods. The proposed method improved both factor estimation and proportions extraction for specific binding. Modeling the variability of the specific binding factor has a strong potential impact for dynamic PET image analysis.

Hierarchical Bayesian image analysis: from low-level modeling to robust supervised learning

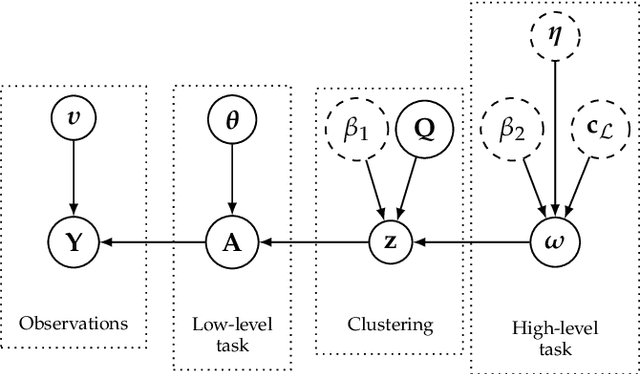
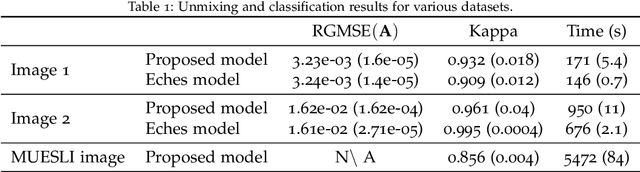
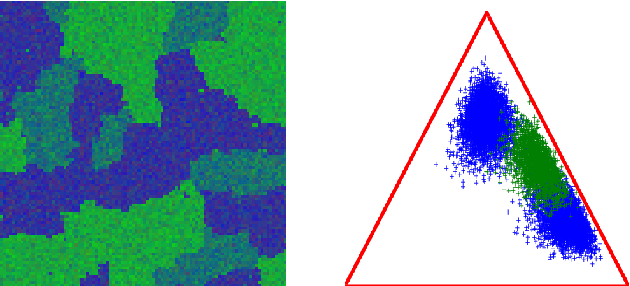
Within a supervised classification framework, labeled data are used to learn classifier parameters. Prior to that, it is generally required to perform dimensionality reduction via feature extraction. These preprocessing steps have motivated numerous research works aiming at recovering latent variables in an unsupervised context. This paper proposes a unified framework to perform classification and low-level modeling jointly. The main objective is to use the estimated latent variables as features for classification and to incorporate simultaneously supervised information to help latent variable extraction. The proposed hierarchical Bayesian model is divided into three stages: a first low-level modeling stage to estimate latent variables, a second stage clustering these features into statistically homogeneous groups and a last classification stage exploiting the (possibly badly) labeled data. Performance of the model is assessed in the specific context of hyperspectral image interpretation, unifying two standard analysis techniques, namely unmixing and classification.

Bayesian nonparametric Principal Component Analysis

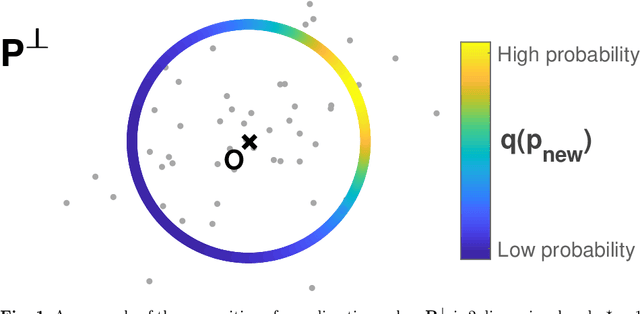
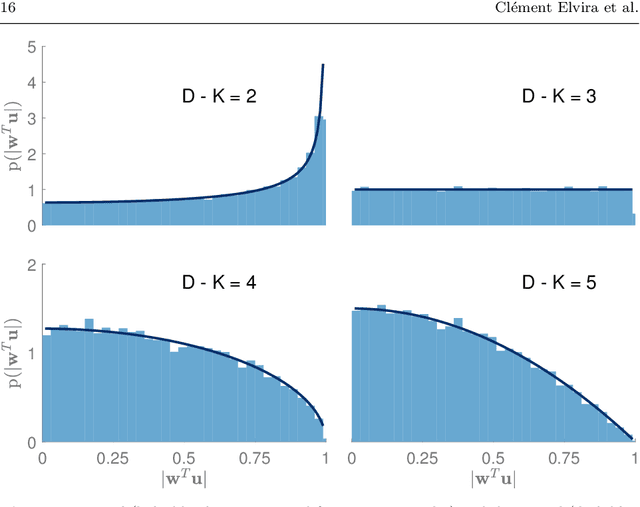
Principal component analysis (PCA) is very popular to perform dimension reduction. The selection of the number of significant components is essential but often based on some practical heuristics depending on the application. Only few works have proposed a probabilistic approach able to infer the number of significant components. To this purpose, this paper introduces a Bayesian nonparametric principal component analysis (BNP-PCA). The proposed model projects observations onto a random orthogonal basis which is assigned a prior distribution defined on the Stiefel manifold. The prior on factor scores involves an Indian buffet process to model the uncertainty related to the number of components. The parameters of interest as well as the nuisance parameters are finally inferred within a fully Bayesian framework via Monte Carlo sampling. A study of the (in-)consistence of the marginal maximum a posteriori estimator of the latent dimension is carried out. A new estimator of the subspace dimension is proposed. Moreover, for sake of statistical significance, a Kolmogorov-Smirnov test based on the posterior distribution of the principal components is used to refine this estimate. The behaviour of the algorithm is first studied on various synthetic examples. Finally, the proposed BNP dimension reduction approach is shown to be easily yet efficiently coupled with clustering or latent factor models within a unique framework.

Bayesian selection for the l2-Potts model regularization parameter: 1D piecewise constant signal denoising

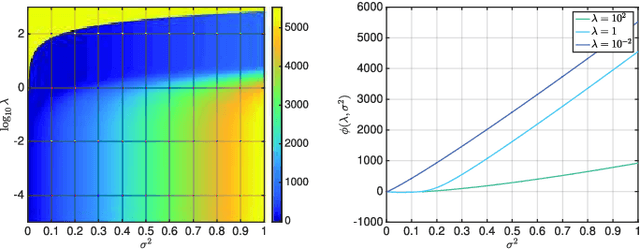
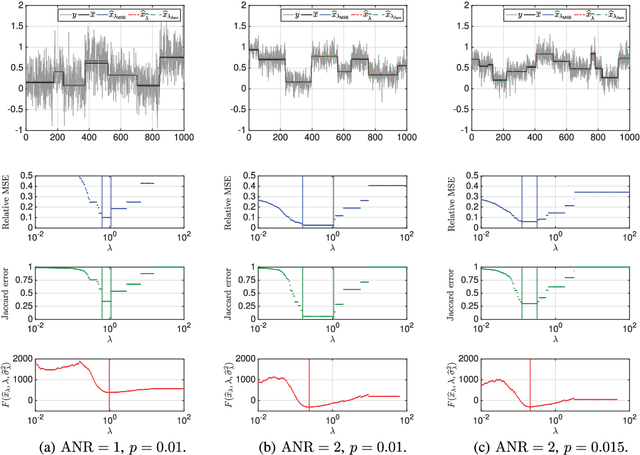
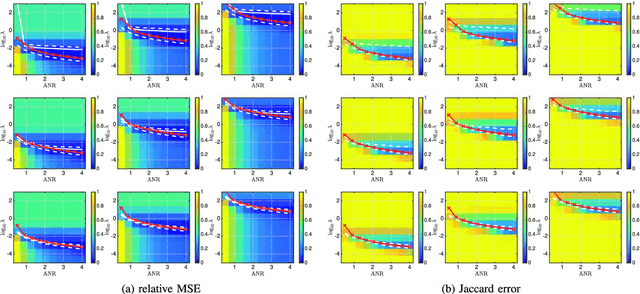
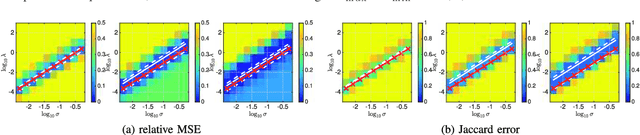
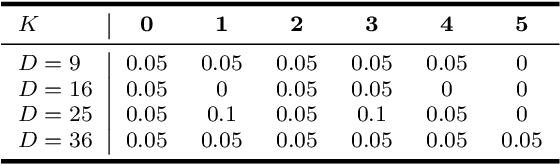
Piecewise constant denoising can be solved either by deterministic optimization approaches, based on the Potts model, or by stochastic Bayesian procedures. The former lead to low computational time but require the selection of a regularization parameter, whose value significantly impacts the achieved solution, and whose automated selection remains an involved and challenging problem. Conversely, fully Bayesian formalisms encapsulate the regularization parameter selection into hierarchical models, at the price of high computational costs. This contribution proposes an operational strategy that combines hierarchical Bayesian and Potts model formulations, with the double aim of automatically tuning the regularization parameter and of maintaining computational effciency. The proposed procedure relies on formally connecting a Bayesian framework to a l2-Potts functional. Behaviors and performance for the proposed piecewise constant denoising and regularization parameter tuning techniques are studied qualitatively and assessed quantitatively, and shown to compare favorably against those of a fully Bayesian hierarchical procedure, both in accuracy and in computational load.

Robust Fusion of Multi-Band Images with Different Spatial and Spectral Resolutions for Change Detection

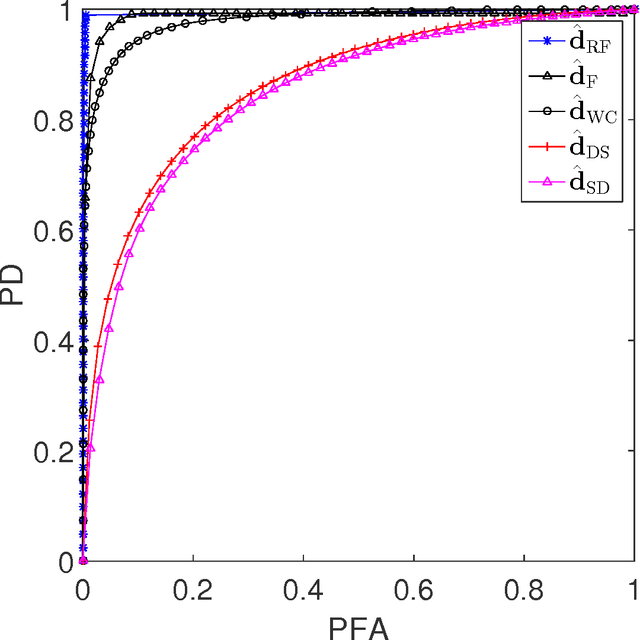
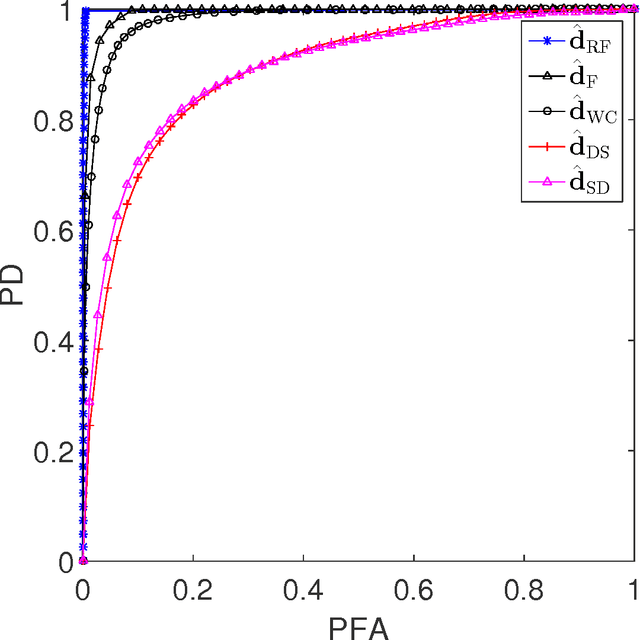
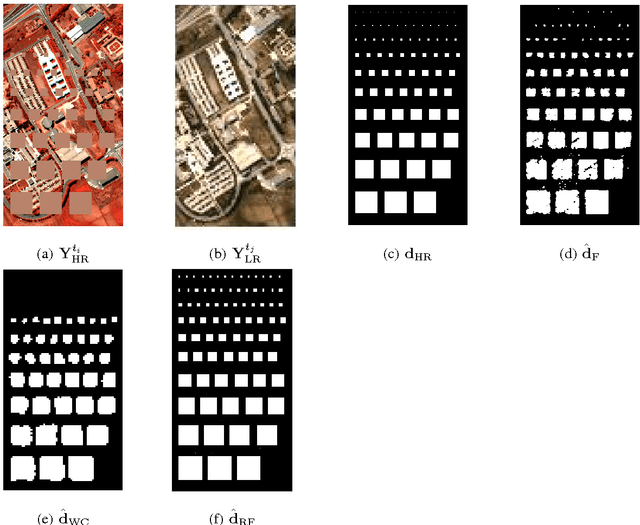
Archetypal scenarios for change detection generally consider two images acquired through sensors of the same modality. However, in some specific cases such as emergency situations, the only images available may be those acquired through different kinds of sensors. More precisely, this paper addresses the problem of detecting changes between two multi-band optical images characterized by different spatial and spectral resolutions. This sensor dissimilarity introduces additional issues in the context of operational change detection. To alleviate these issues, classical change detection methods are applied after independent preprocessing steps (e.g., resampling) used to get the same spatial and spectral resolutions for the pair of observed images. Nevertheless, these preprocessing steps tend to throw away relevant information. Conversely, in this paper, we propose a method that more effectively uses the available information by modeling the two observed images as spatial and spectral versions of two (unobserved) latent images characterized by the same high spatial and high spectral resolutions. As they cover the same scene, these latent images are expected to be globally similar except for possible changes in sparse spatial locations. Thus, the change detection task is envisioned through a robust multi-band image fusion method which enforces the differences between the estimated latent images to be spatially sparse. This robust fusion problem is formulated as an inverse problem which is iteratively solved using an efficient block-coordinate descent algorithm. The proposed method is applied to real panchormatic/multispectral and hyperspectral images with simulated realistic changes. A comparison with state-of-the-art change detection methods evidences the accuracy of the proposed strategy.