Hybrid Quantum-Classical Multi-Agent Pathfinding

Multi-Agent Path Finding (MAPF) focuses on determining conflict-free paths for multiple agents navigating through a shared space to reach specified goal locations. This problem becomes computationally challenging, particularly when handling large numbers of agents, as frequently encountered in practical applications like coordinating autonomous vehicles. Quantum computing (QC) is a promising candidate in overcoming such limits. However, current quantum hardware is still in its infancy and thus limited in terms of computing power and error robustness. In this work, we present the first optimal hybrid quantum-classical MAPF algorithm which is based on branch-and-cut-and-prize. QC is integrated by iteratively solving QUBO problems, based on conflict graphs. Experiments on actual quantum hardware and results on benchmark data suggest that our approach dominates previous QUBO formulations and baseline MAPF solvers.

Dynamic Range Reduction via Branch-and-Bound

The demand for high-performance computing in machine learning and artificial intelligence has led to the development of specialized hardware accelerators like Tensor Processing Units (TPUs), Graphics Processing Units (GPUs), and Field-Programmable Gate Arrays (FPGAs). A key strategy to enhance these accelerators is the reduction of precision in arithmetic operations, which increases processing speed and lowers latency - crucial for real-time AI applications. Precision reduction minimizes memory bandwidth requirements and energy consumption, essential for large-scale and mobile deployments, and increases throughput by enabling more parallel operations per cycle, maximizing hardware resource utilization. This strategy is equally vital for solving NP-hard quadratic unconstrained binary optimization (QUBO) problems common in machine learning, which often require high precision for accurate representation. Special hardware solvers, such as quantum annealers, benefit significantly from precision reduction. This paper introduces a fully principled Branch-and-Bound algorithm for reducing precision needs in QUBO problems by utilizing dynamic range as a measure of complexity. Experiments validate our algorithm's effectiveness on an actual quantum annealer.

Computing Marginal and Conditional Divergences between Decomposable Models with Applications

The ability to compute the exact divergence between two high-dimensional distributions is useful in many applications but doing so naively is intractable. Computing the alpha-beta divergence -- a family of divergences that includes the Kullback-Leibler divergence and Hellinger distance -- between the joint distribution of two decomposable models, i.e chordal Markov networks, can be done in time exponential in the treewidth of these models. However, reducing the dissimilarity between two high-dimensional objects to a single scalar value can be uninformative. Furthermore, in applications such as supervised learning, the divergence over a conditional distribution might be of more interest. Therefore, we propose an approach to compute the exact alpha-beta divergence between any marginal or conditional distribution of two decomposable models. Doing so tractably is non-trivial as we need to decompose the divergence between these distributions and therefore, require a decomposition over the marginal and conditional distributions of these models. Consequently, we provide such a decomposition and also extend existing work to compute the marginal and conditional alpha-beta divergence between these decompositions. We then show how our method can be used to analyze distributional changes by first applying it to a benchmark image dataset. Finally, based on our framework, we propose a novel way to quantify the error in contemporary superconducting quantum computers. Code for all experiments is available at: https://lklee.dev/pub/2023-icdm/code

Explainable Quantum Machine Learning

Methods of artificial intelligence (AI) and especially machine learning (ML) have been growing ever more complex, and at the same time have more and more impact on people's lives. This leads to explainable AI (XAI) manifesting itself as an important research field that helps humans to better comprehend ML systems. In parallel, quantum machine learning (QML) is emerging with the ongoing improvement of quantum computing hardware combined with its increasing availability via cloud services. QML enables quantum-enhanced ML in which quantum mechanics is exploited to facilitate ML tasks, typically in form of quantum-classical hybrid algorithms that combine quantum and classical resources. Quantum gates constitute the building blocks of gate-based quantum hardware and form circuits that can be used for quantum computations. For QML applications, quantum circuits are typically parameterized and their parameters are optimized classically such that a suitably defined objective function is minimized. Inspired by XAI, we raise the question of explainability of such circuits by quantifying the importance of (groups of) gates for specific goals. To this end, we transfer and adapt the well-established concept of Shapley values to the quantum realm. The resulting attributions can be interpreted as explanations for why a specific circuit works well for a given task, improving the understanding of how to construct parameterized (or variational) quantum circuits, and fostering their human interpretability in general. An experimental evaluation on simulators and two superconducting quantum hardware devices demonstrates the benefits of the proposed framework for classification, generative modeling, transpilation, and optimization. Furthermore, our results shed some light on the role of specific gates in popular QML approaches.

Shapley Values with Uncertain Value Functions

We propose a novel definition of Shapley values with uncertain value functions based on first principles using probability theory. Such uncertain value functions can arise in the context of explainable machine learning as a result of non-deterministic algorithms. We show that random effects can in fact be absorbed into a Shapley value with a noiseless but shifted value function. Hence, Shapley values with uncertain value functions can be used in analogy to regular Shapley values. However, their reliable evaluation typically requires more computational effort.

Full Kullback-Leibler-Divergence Loss for Hyperparameter-free Label Distribution Learning

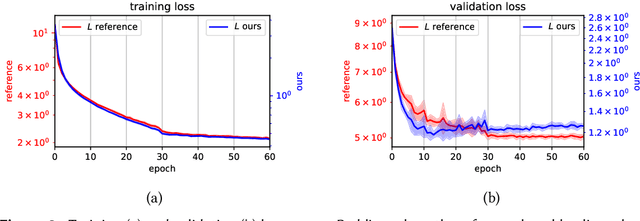
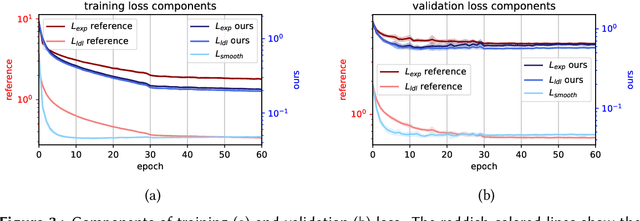
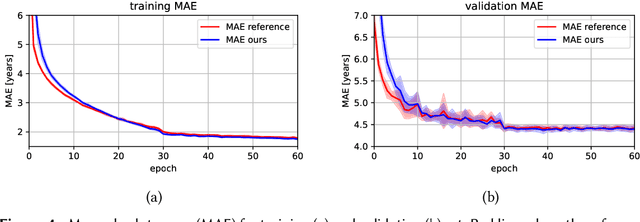
The concept of Label Distribution Learning (LDL) is a technique to stabilize classification and regression problems with ambiguous and/or imbalanced labels. A prototypical use-case of LDL is human age estimation based on profile images. Regarding this regression problem, a so called Deep Label Distribution Learning (DLDL) method has been developed. The main idea is the joint regression of the label distribution and its expectation value. However, the original DLDL method uses loss components with different mathematical motivation and, thus, different scales, which is why the use of a hyperparameter becomes necessary. In this work, we introduce a loss function for DLDL whose components are completely defined by Kullback-Leibler (KL) divergences and, thus, are directly comparable to each other without the need of additional hyperparameters. It generalizes the concept of DLDL with regard to further use-cases, in particular for multi-dimensional or multi-scale distribution learning tasks.

On Quantum Circuits for Discrete Graphical Models

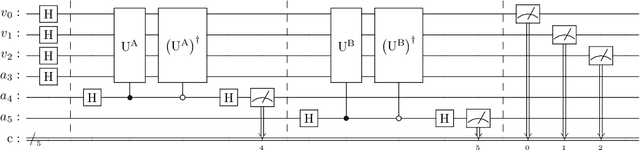
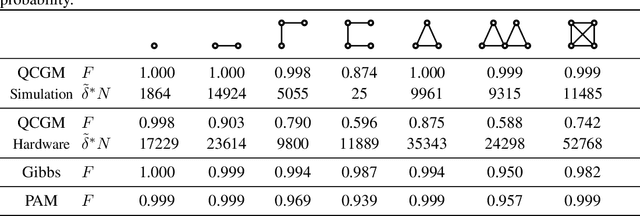
Graphical models are useful tools for describing structured high-dimensional probability distributions. Development of efficient algorithms for generating unbiased and independent samples from graphical models remains an active research topic. Sampling from graphical models that describe the statistics of discrete variables is a particularly challenging problem, which is intractable in the presence of high dimensions. In this work, we provide the first method that allows one to provably generate unbiased and independent samples from general discrete factor models with a quantum circuit. Our method is compatible with multi-body interactions and its success probability does not depend on the number of variables. To this end, we identify a novel embedding of the graphical model into unitary operators and provide rigorous guarantees on the resulting quantum state. Moreover, we prove a unitary Hammersley-Clifford theorem -- showing that our quantum embedding factorizes over the cliques of the underlying conditional independence structure. Importantly, the quantum embedding allows for maximum likelihood learning as well as maximum a posteriori state approximation via state-of-the-art hybrid quantum-classical methods. Finally, the proposed quantum method can be implemented on current quantum processors. Experiments with quantum simulation as well as actual quantum hardware show that our method can carry out sampling and parameter learning on quantum computers.

Informed Pre-Training on Prior Knowledge

When training data is scarce, the incorporation of additional prior knowledge can assist the learning process. While it is common to initialize neural networks with weights that have been pre-trained on other large data sets, pre-training on more concise forms of knowledge has rather been overlooked. In this paper, we propose a novel informed machine learning approach and suggest to pre-train on prior knowledge. Formal knowledge representations, e.g. graphs or equations, are first transformed into a small and condensed data set of knowledge prototypes. We show that informed pre-training on such knowledge prototypes (i) speeds up the learning processes, (ii) improves generalization capabilities in the regime where not enough training data is available, and (iii) increases model robustness. Analyzing which parts of the model are affected most by the prototypes reveals that improvements come from deeper layers that typically represent high-level features. This confirms that informed pre-training can indeed transfer semantic knowledge. This is a novel effect, which shows that knowledge-based pre-training has additional and complementary strengths to existing approaches.

Towards Bundle Adjustment for Satellite Imaging via Quantum Machine Learning

Given is a set of images, where all images show views of the same area at different points in time and from different viewpoints. The task is the alignment of all images such that relevant information, e.g., poses, changes, and terrain, can be extracted from the fused image. In this work, we focus on quantum methods for keypoint extraction and feature matching, due to the demanding computational complexity of these sub-tasks. To this end, k-medoids clustering, kernel density clustering, nearest neighbor search, and kernel methods are investigated and it is explained how these methods can be re-formulated for quantum annealers and gate-based quantum computers. Experimental results obtained on digital quantum emulation hardware, quantum annealers, and quantum gate computers show that classical systems still deliver superior results. However, the proposed methods are ready for the current and upcoming generations of quantum computing devices which have the potential to outperform classical systems in the near future.

Quantum Feature Selection

In machine learning, fewer features reduce model complexity. Carefully assessing the influence of each input feature on the model quality is therefore a crucial preprocessing step. We propose a novel feature selection algorithm based on a quadratic unconstrained binary optimization (QUBO) problem, which allows to select a specified number of features based on their importance and redundancy. In contrast to iterative or greedy methods, our direct approach yields higherquality solutions. QUBO problems are particularly interesting because they can be solved on quantum hardware. To evaluate our proposed algorithm, we conduct a series of numerical experiments using a classical computer, a quantum gate computer and a quantum annealer. Our evaluation compares our method to a range of standard methods on various benchmark datasets. We observe competitive performance.