The Origins of Representation Manifolds in Large Language Models

There is a large ongoing scientific effort in mechanistic interpretability to map embeddings and internal representations of AI systems into human-understandable concepts. A key element of this effort is the linear representation hypothesis, which posits that neural representations are sparse linear combinations of `almost-orthogonal' direction vectors, reflecting the presence or absence of different features. This model underpins the use of sparse autoencoders to recover features from representations. Moving towards a fuller model of features, in which neural representations could encode not just the presence but also a potentially continuous and multidimensional value for a feature, has been a subject of intense recent discourse. We describe why and how a feature might be represented as a manifold, demonstrating in particular that cosine similarity in representation space may encode the intrinsic geometry of a feature through shortest, on-manifold paths, potentially answering the question of how distance in representation space and relatedness in concept space could be connected. The critical assumptions and predictions of the theory are validated on text embeddings and token activations of large language models.

How high is `high'? Rethinking the roles of dimensionality in topological data analysis and manifold learning

We present a generalised Hanson-Wright inequality and use it to establish new statistical insights into the geometry of data point-clouds. In the setting of a general random function model of data, we clarify the roles played by three notions of dimensionality: ambient intrinsic dimension $p_{\mathrm{int}}$, which measures total variability across orthogonal feature directions; correlation rank, which measures functional complexity across samples; and latent intrinsic dimension, which is the dimension of manifold structure hidden in data. Our analysis shows that in order for persistence diagrams to reveal latent homology and for manifold structure to emerge it is sufficient that $p_{\mathrm{int}}\gg \log n$, where $n$ is the sample size. Informed by these theoretical perspectives, we revisit the ground-breaking neuroscience discovery of toroidal structure in grid-cell activity made by Gardner et al. (Nature, 2022): our findings reveal, for the first time, evidence that this structure is in fact isometric to physical space, meaning that grid cell activity conveys a geometrically faithful representation of the real world.

Conditional Distribution Compression via the Kernel Conditional Mean Embedding

Existing distribution compression methods, like Kernel Herding (KH), were originally developed for unlabelled data. However, no existing approach directly compresses the conditional distribution of labelled data. To address this gap, we first introduce the Average Maximum Conditional Mean Discrepancy (AMCMD), a natural metric for comparing conditional distributions. We then derive a consistent estimator for the AMCMD and establish its rate of convergence. Next, we make a key observation: in the context of distribution compression, the cost of constructing a compressed set targeting the AMCMD can be reduced from $\mathcal{O}(n^3)$ to $\mathcal{O}(n)$. Building on this, we extend the idea of KH to develop Average Conditional Kernel Herding (ACKH), a linear-time greedy algorithm that constructs a compressed set targeting the AMCMD. To better understand the advantages of directly compressing the conditional distribution rather than doing so via the joint distribution, we introduce Joint Kernel Herding (JKH), a straightforward adaptation of KH designed to compress the joint distribution of labelled data. While herding methods provide a simple and interpretable selection process, they rely on a greedy heuristic. To explore alternative optimisation strategies, we propose Joint Kernel Inducing Points (JKIP) and Average Conditional Kernel Inducing Points (ACKIP), which jointly optimise the compressed set while maintaining linear complexity. Experiments show that directly preserving conditional distributions with ACKIP outperforms both joint distribution compression (via JKH and JKIP) and the greedy selection used in ACKH. Moreover, we see that JKIP consistently outperforms JKH.

Intensity Profile Projection: A Framework for Continuous-Time Representation Learning for Dynamic Networks

We present a new algorithmic framework, Intensity Profile Projection, for learning continuous-time representations of the nodes of a dynamic network, characterised by a node set and a collection of instantaneous interaction events which occur in continuous time. Our framework consists of three stages: estimating the intensity functions underlying the interactions between pairs of nodes, e.g. via kernel smoothing; learning a projection which minimises a notion of intensity reconstruction error; and inductively constructing evolving node representations via the learned projection. We show that our representations preserve the underlying structure of the network, and are temporally coherent, meaning that node representations can be meaningfully compared at different points in time. We develop estimation theory which elucidates the role of smoothing as a bias-variance trade-off, and shows how we can reduce smoothing as the signal-to-noise ratio increases on account of the algorithm `borrowing strength' across the network.

Hierarchical clustering with dot products recovers hidden tree structure

In this paper we offer a new perspective on the well established agglomerative clustering algorithm, focusing on recovery of hierarchical structure. We recommend a simple variant of the standard algorithm, in which clusters are merged by maximum average dot product and not, for example, by minimum distance or within-cluster variance. We demonstrate that the tree output by this algorithm provides a bona fide estimate of generative hierarchical structure in data, under a generic probabilistic graphical model. The key technical innovations are to understand how hierarchical information in this model translates into tree geometry which can be recovered from data, and to characterise the benefits of simultaneously growing sample size and data dimension. We demonstrate superior tree recovery performance with real data over existing approaches such as UPGMA, Ward's method, and HDBSCAN.

Implications of sparsity and high triangle density for graph representation learning

Recent work has shown that sparse graphs containing many triangles cannot be reproduced using a finite-dimensional representation of the nodes, in which link probabilities are inner products. Here, we show that such graphs can be reproduced using an infinite-dimensional inner product model, where the node representations lie on a low-dimensional manifold. Recovering a global representation of the manifold is impossible in a sparse regime. However, we can zoom in on local neighbourhoods, where a lower-dimensional representation is possible. As our constructions allow the points to be uniformly distributed on the manifold, we find evidence against the common perception that triangles imply community structure.

Consistent and fast inference in compartmental models of epidemics using Poisson Approximate Likelihoods

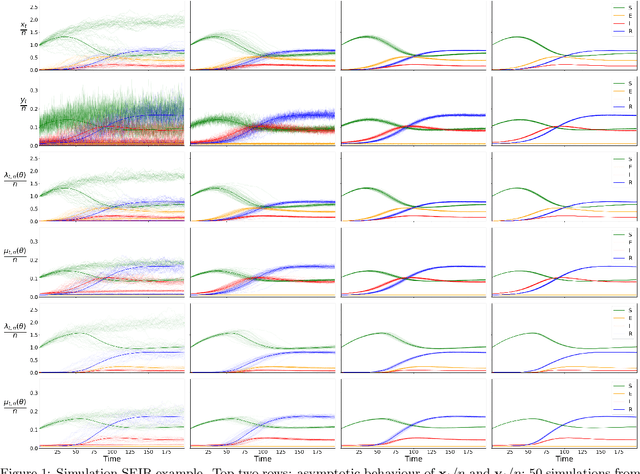
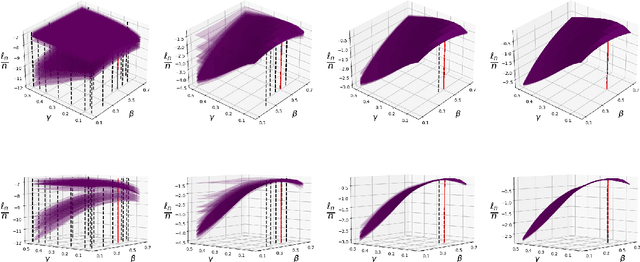
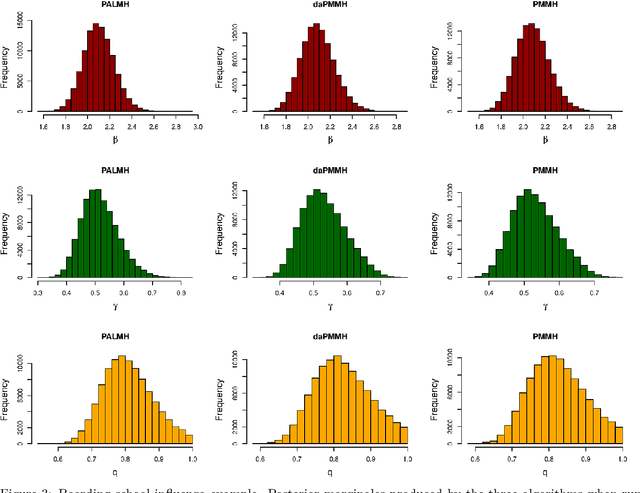
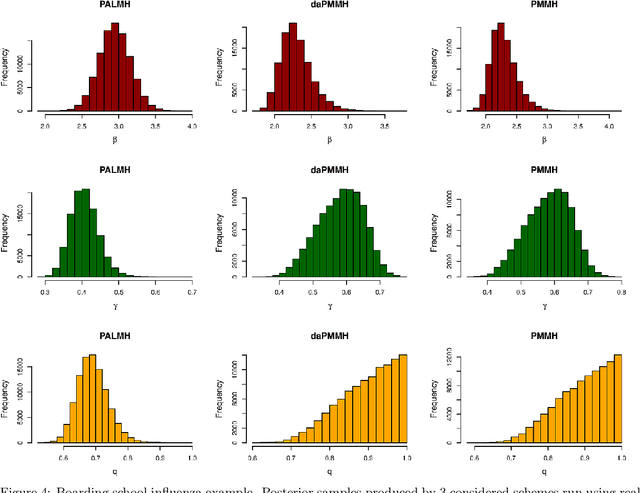
Addressing the challenge of scaling-up epidemiological inference to complex and heterogeneous models, we introduce Poisson Approximate Likelihood (PAL) methods. In contrast to the popular ODE approach to compartmental modelling, in which a large population limit is used to motivate a deterministic model, PALs are derived from approximate filtering equations for finite-population, stochastic compartmental models, and the large population limit drives the consistency of maximum PAL estimators. Our theoretical results appear to be the first likelihood-based parameter estimation consistency results applicable across a broad class of partially observed stochastic compartmental models. Compared to simulation-based methods such as Approximate Bayesian Computation and Sequential Monte Carlo, PALs are simple to implement, involving only elementary arithmetic operations and no tuning parameters; and fast to evaluate, requiring no simulation from the model and having computational cost independent of population size. Through examples, we demonstrate how PALs can be: embedded within Delayed Acceptance Particle Markov Chain Monte Carlo to facilitate Bayesian inference; used to fit an age-structured model of influenza, taking advantage of automatic differentiation in Stan; and applied to calibrate a spatial meta-population model of measles.

Matrix factorisation and the interpretation of geodesic distance

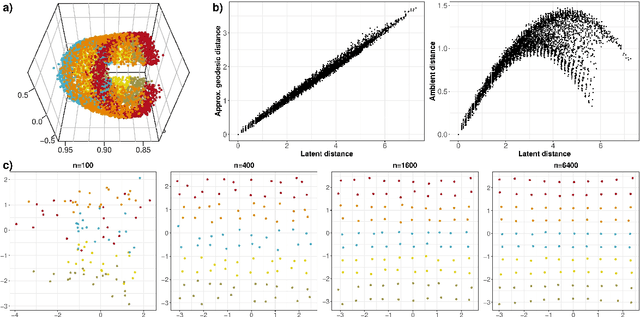
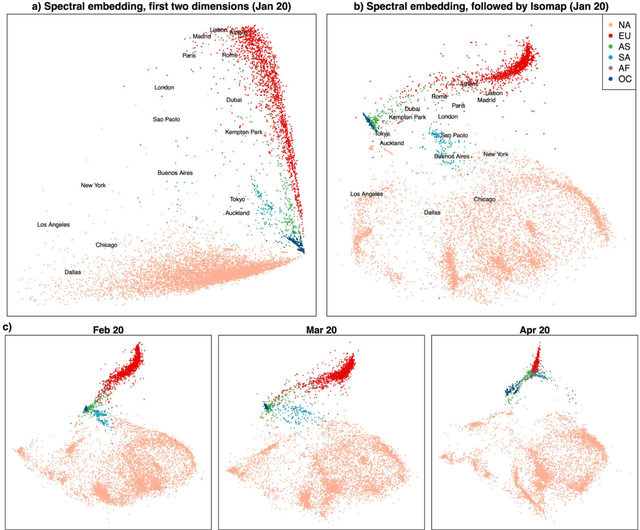
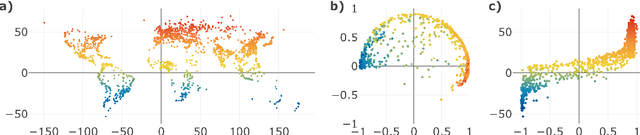
Given a graph or similarity matrix, we consider the problem of recovering a notion of true distance between the nodes, and so their true positions. Through new insights into the manifold geometry underlying a generic latent position model, we show that this can be accomplished in two steps: matrix factorisation, followed by nonlinear dimension reduction. This combination is effective because the point cloud obtained in the first step lives close to a manifold in which latent distance is encoded as geodesic distance. Hence, a nonlinear dimension reduction tool, approximating geodesic distance, can recover the latent positions, up to a simple transformation. We give a detailed account of the case where spectral embedding is used, followed by Isomap, and provide encouraging experimental evidence for other combinations of techniques.

Inference in Stochastic Epidemic Models via Multinomial Approximations

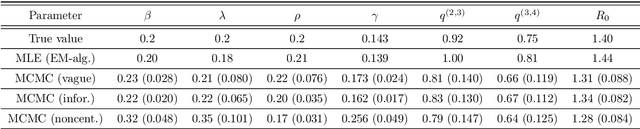
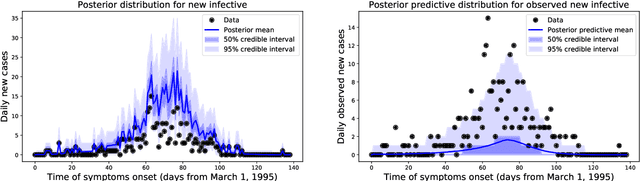
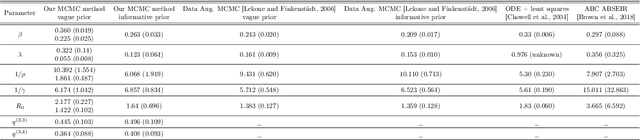
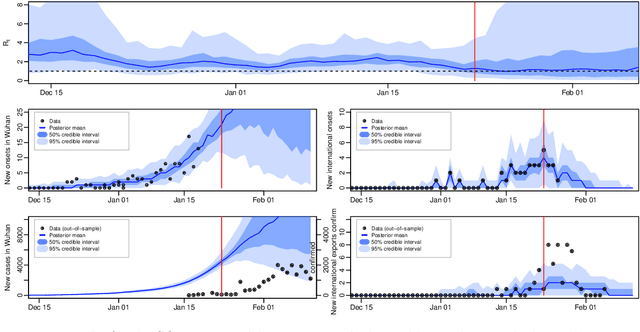
We introduce a new method for inference in stochastic epidemic models which uses recursive multinomial approximations to integrate over unobserved variables and thus circumvent likelihood intractability. The method is applicable to a class of discrete-time, finite-population compartmental models with partial, randomly under-reported or missing count observations. In contrast to state-of-the-art alternatives such as Approximate Bayesian Computation techniques, no forward simulation of the model is required and there are no tuning parameters. Evaluating the approximate marginal likelihood of model parameters is achieved through a computationally simple filtering recursion. The accuracy of the approximation is demonstrated through analysis of real and simulated data using a model of the 1995 Ebola outbreak in the Democratic Republic of Congo. We show how the method can be embedded within a Sequential Monte Carlo approach to estimating the time-varying reproduction number of COVID-19 in Wuhan, China, recently published by Kucharski et al. 2020.

Dynamic Bayesian Neural Networks

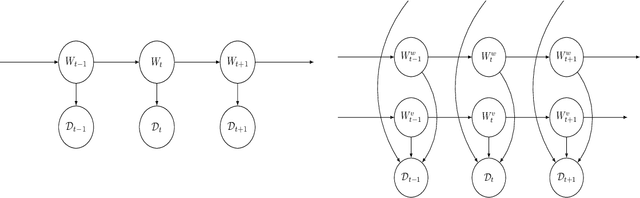
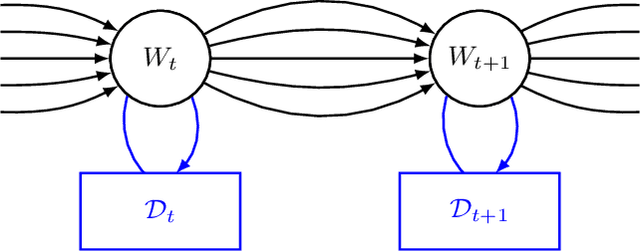
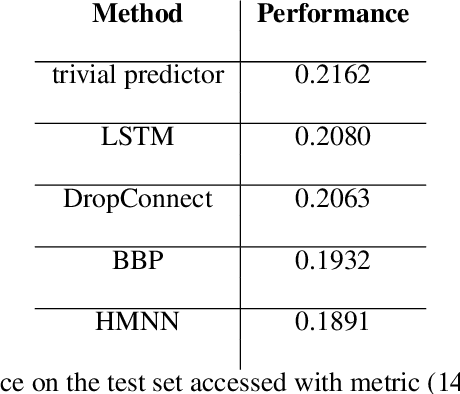
We define an evolving in time Bayesian neural network called a Hidden Markov neural network. The weights of the feed-forward neural network are modelled with the hidden states of a Hidden Markov model, the whose observed process is given by the available data. A filtering algorithm is used to learn a variational approximation to the evolving in time posterior over the weights. Training is pursued through a sequential version of Bayes by Backprop, which is enriched with a stronger regularization technique called variational DropConnect. The experiments are focused on streaming data and time series. On the one hand, we train on MNIST when only a portion of the dataset is available at a time. On the other hand, we perform frames prediction on a waving flag video.