Statistical Reachability Analysis of Stochastic Cyber-Physical Systems under Distribution Shift

Reachability analysis is a popular method to give safety guarantees for stochastic cyber-physical systems (SCPSs) that takes in a symbolic description of the system dynamics and uses set-propagation methods to compute an overapproximation of the set of reachable states over a bounded time horizon. In this paper, we investigate the problem of performing reachability analysis for an SCPS that does not have a symbolic description of the dynamics, but instead is described using a digital twin model that can be simulated to generate system trajectories. An important challenge is that the simulator implicitly models a probability distribution over the set of trajectories of the SCPS; however, it is typical to have a sim2real gap, i.e., the actual distribution of the trajectories in a deployment setting may be shifted from the distribution assumed by the simulator. We thus propose a statistical reachability analysis technique that, given a user-provided threshold $1-\epsilon$, provides a set that guarantees that any reachable state during deployment lies in this set with probability not smaller than this threshold. Our method is based on three main steps: (1) learning a deterministic surrogate model from sampled trajectories, (2) conducting reachability analysis over the surrogate model, and (3) employing {\em robust conformal inference} using an additional set of sampled trajectories to quantify the surrogate model's distribution shift with respect to the deployed SCPS. To counter conservatism in reachable sets, we propose a novel method to train surrogate models that minimizes a quantile loss term (instead of the usual mean squared loss), and a new method that provides tighter guarantees using conformal inference using a normalized surrogate error. We demonstrate the effectiveness of our technique on various case studies.

Scaling Learning based Policy Optimization for Temporal Tasks via Dropout

This paper introduces a model-based approach for training feedback controllers for an autonomous agent operating in a highly nonlinear environment. We desire the trained policy to ensure that the agent satisfies specific task objectives, expressed in discrete-time Signal Temporal Logic (DT-STL). One advantage for reformulation of a task via formal frameworks, like DT-STL, is that it permits quantitative satisfaction semantics. In other words, given a trajectory and a DT-STL formula, we can compute the robustness, which can be interpreted as an approximate signed distance between the trajectory and the set of trajectories satisfying the formula. We utilize feedback controllers, and we assume a feed forward neural network for learning these feedback controllers. We show how this learning problem is similar to training recurrent neural networks (RNNs), where the number of recurrent units is proportional to the temporal horizon of the agent's task objectives. This poses a challenge: RNNs are susceptible to vanishing and exploding gradients, and na\"{i}ve gradient descent-based strategies to solve long-horizon task objectives thus suffer from the same problems. To tackle this challenge, we introduce a novel gradient approximation algorithm based on the idea of dropout or gradient sampling. We show that, the existing smooth semantics for robustness are inefficient regarding gradient computation when the specification becomes complex. To address this challenge, we propose a new smooth semantics for DT-STL that under-approximates the robustness value and scales well for backpropagation over a complex specification. We show that our control synthesis methodology, can be quite helpful for stochastic gradient descent to converge with less numerical issues, enabling scalable backpropagation over long time horizons and trajectories over high dimensional state spaces.

Data-Driven Reachability Analysis of Stochastic Dynamical Systems with Conformal Inference

We consider data-driven reachability analysis of discrete-time stochastic dynamical systems using conformal inference. We assume that we are not provided with a symbolic representation of the stochastic system, but instead have access to a dataset of $K$-step trajectories. The reachability problem is to construct a probabilistic flowpipe such that the probability that a $K$-step trajectory can violate the bounds of the flowpipe does not exceed a user-specified failure probability threshold. The key ideas in this paper are: (1) to learn a surrogate predictor model from data, (2) to perform reachability analysis using the surrogate model, and (3) to quantify the surrogate model's incurred error using conformal inference in order to give probabilistic reachability guarantees. We focus on learning-enabled control systems with complex closed-loop dynamics that are difficult to model symbolically, but where state transition pairs can be queried, e.g., using a simulator. We demonstrate the applicability of our method on examples from the domain of learning-enabled cyber-physical systems.

Convex Optimization-based Policy Adaptation to Compensate for Distributional Shifts

Many real-world systems often involve physical components or operating environments with highly nonlinear and uncertain dynamics. A number of different control algorithms can be used to design optimal controllers for such systems, assuming a reasonably high-fidelity model of the actual system. However, the assumptions made on the stochastic dynamics of the model when designing the optimal controller may no longer be valid when the system is deployed in the real-world. The problem addressed by this paper is the following: Suppose we obtain an optimal trajectory by solving a control problem in the training environment, how do we ensure that the real-world system trajectory tracks this optimal trajectory with minimal amount of error in a deployment environment. In other words, we want to learn how we can adapt an optimal trained policy to distribution shifts in the environment. Distribution shifts are problematic in safety-critical systems, where a trained policy may lead to unsafe outcomes during deployment. We show that this problem can be cast as a nonlinear optimization problem that could be solved using heuristic method such as particle swarm optimization (PSO). However, if we instead consider a convex relaxation of this problem, we can learn policies that track the optimal trajectory with much better error performance, and faster computation times. We demonstrate the efficacy of our approach on tracking an optimal path using a Dubin's car model, and collision avoidance using both a linear and nonlinear model for adaptive cruise control.

A Neurosymbolic Approach to the Verification of Temporal Logic Properties of Learning enabled Control Systems

Signal Temporal Logic (STL) has become a popular tool for expressing formal requirements of Cyber-Physical Systems (CPS). The problem of verifying STL properties of neural network-controlled CPS remains a largely unexplored problem. In this paper, we present a model for the verification of Neural Network (NN) controllers for general STL specifications using a custom neural architecture where we map an STL formula into a feed-forward neural network with ReLU activation. In the case where both our plant model and the controller are ReLU-activated neural networks, we reduce the STL verification problem to reachability in ReLU neural networks. We also propose a new approach for neural network controllers with general activation functions; this approach is a sound and complete verification approach based on computing the Lipschitz constant of the closed-loop control system. We demonstrate the practical efficacy of our techniques on a number of examples of learning-enabled control systems.

Risk-Awareness in Learning Neural Controllers for Temporal Logic Objectives

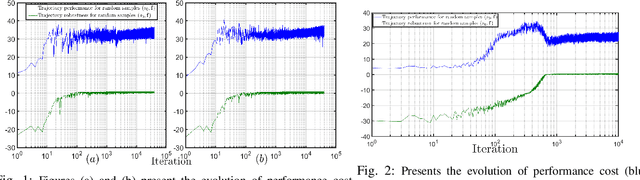
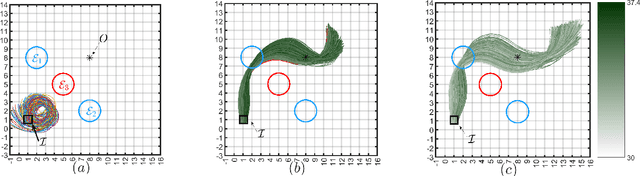
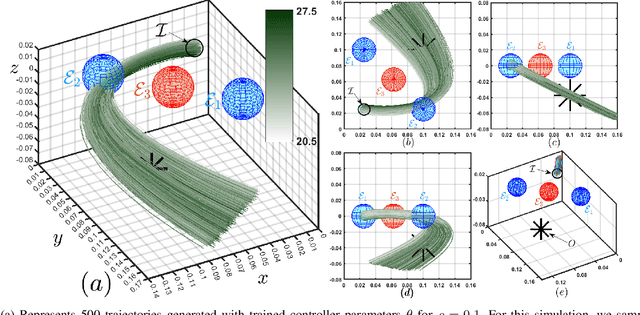
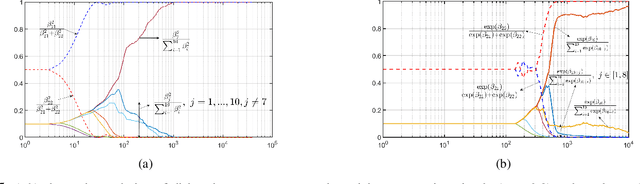
In this paper, we consider the problem of synthesizing a controller in the presence of uncertainty such that the resulting closed-loop system satisfies certain hard constraints while optimizing certain (soft) performance objectives. We assume that the hard constraints encoding safety or mission-critical task objectives are expressed using Signal Temporal Logic (STL), while performance is quantified using standard cost functions on system trajectories. In order to prioritize the satisfaction of the hard STL constraints, we utilize the framework of control barrier functions (CBFs) and algorithmically obtain CBFs for STL objectives. We assume that the controllers are modeled using neural networks (NNs) and provide an optimization algorithm to learn the optimal parameters for the NN controller that optimize the performance at a user-specified robustness margin for the safety specifications. We use the formalism of risk measures to evaluate the risk incurred by the trade-off between robustness margin of the system and its performance. We demonstrate the efficacy of our approach on well-known difficult examples for nonlinear control such as a quad-rotor and a unicycle, where the mission objectives for each system include hard timing constraints and safety objectives.

Performance Bounds for Neural Network Estimators: Applications in Fault Detection

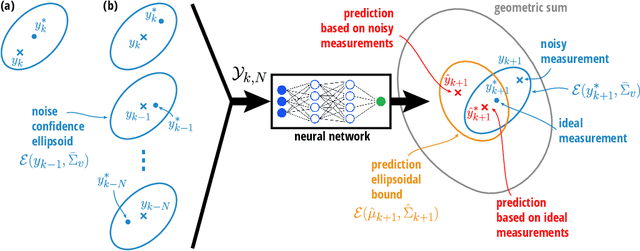
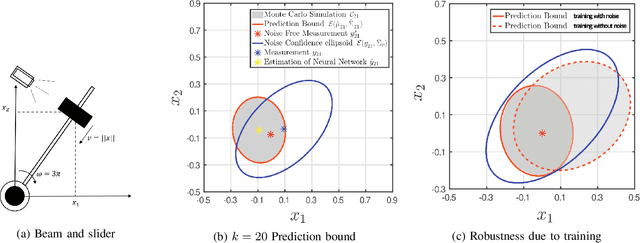
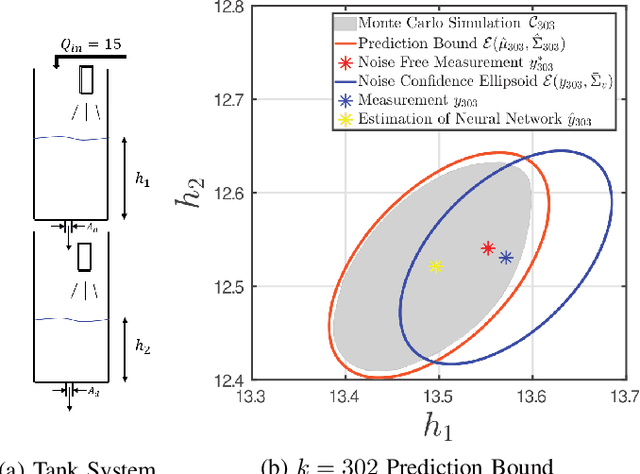
We exploit recent results in quantifying the robustness of neural networks to input variations to construct and tune a model-based anomaly detector, where the data-driven estimator model is provided by an autoregressive neural network. In tuning, we specifically provide upper bounds on the rate of false alarms expected under normal operation. To accomplish this, we provide a theory extension to allow for the propagation of multiple confidence ellipsoids through a neural network. The ellipsoid that bounds the output of the neural network under the input variation informs the sensitivity - and thus the threshold tuning - of the detector. We demonstrate this approach on a linear and nonlinear dynamical system.

Certifying Incremental Quadratic Constraints for Neural Networks via Convex Optimization

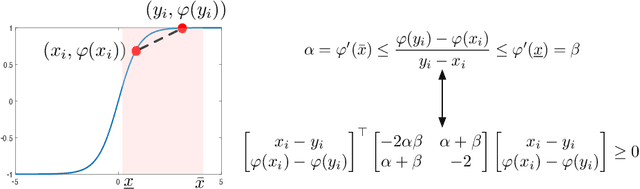
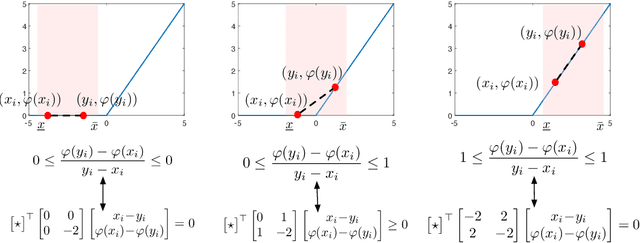
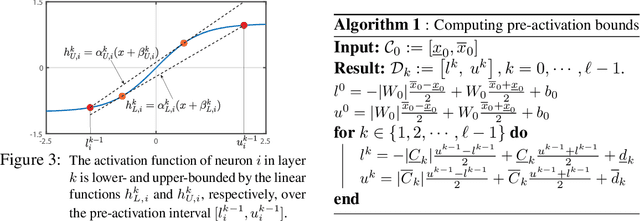
Abstracting neural networks with constraints they impose on their inputs and outputs can be very useful in the analysis of neural network classifiers and to derive optimization-based algorithms for certification of stability and robustness of feedback systems involving neural networks. In this paper, we propose a convex program, in the form of a Linear Matrix Inequality (LMI), to certify incremental quadratic constraints on the map of neural networks over a region of interest. These certificates can capture several useful properties such as (local) Lipschitz continuity, one-sided Lipschitz continuity, invertibility, and contraction. We illustrate the utility of our approach in two different settings. First, we develop a semidefinite program to compute guaranteed and sharp upper bounds on the local Lipschitz constant of neural networks and illustrate the results on random networks as well as networks trained on MNIST. Second, we consider a linear time-invariant system in feedback with an approximate model predictive controller parameterized by a neural network. We then turn the stability analysis into a semidefinite feasibility program and estimate an ellipsoidal invariant set for the closed-loop system.