Probabilistic Label Relation Graphs with Ising Models

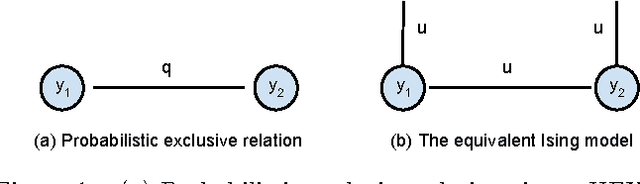
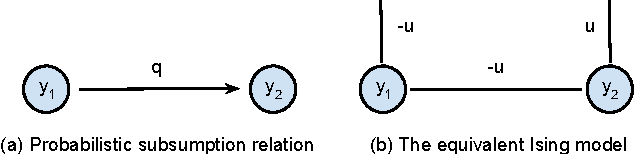
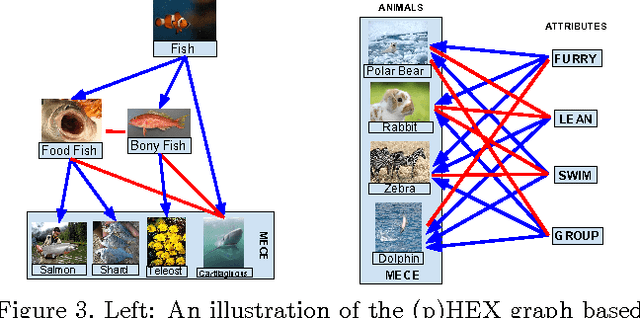
We consider classification problems in which the label space has structure. A common example is hierarchical label spaces, corresponding to the case where one label subsumes another (e.g., animal subsumes dog). But labels can also be mutually exclusive (e.g., dog vs cat) or unrelated (e.g., furry, carnivore). To jointly model hierarchy and exclusion relations, the notion of a HEX (hierarchy and exclusion) graph was introduced in [7]. This combined a conditional random field (CRF) with a deep neural network (DNN), resulting in state of the art results when applied to visual object classification problems where the training labels were drawn from different levels of the ImageNet hierarchy (e.g., an image might be labeled with the basic level category "dog", rather than the more specific label "husky"). In this paper, we extend the HEX model to allow for soft or probabilistic relations between labels, which is useful when there is uncertainty about the relationship between two labels (e.g., an antelope is "sort of" furry, but not to the same degree as a grizzly bear). We call our new model pHEX, for probabilistic HEX. We show that the pHEX graph can be converted to an Ising model, which allows us to use existing off-the-shelf inference methods (in contrast to the HEX method, which needed specialized inference algorithms). Experimental results show significant improvements in a number of large-scale visual object classification tasks, outperforming the previous HEX model.

Totally Corrective Boosting with Cardinality Penalization

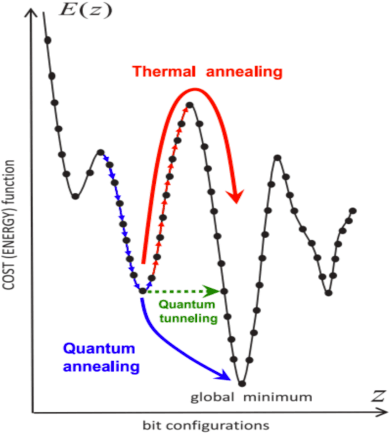
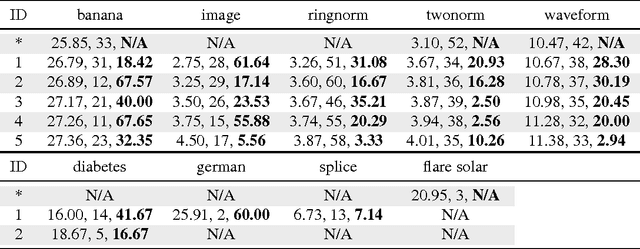
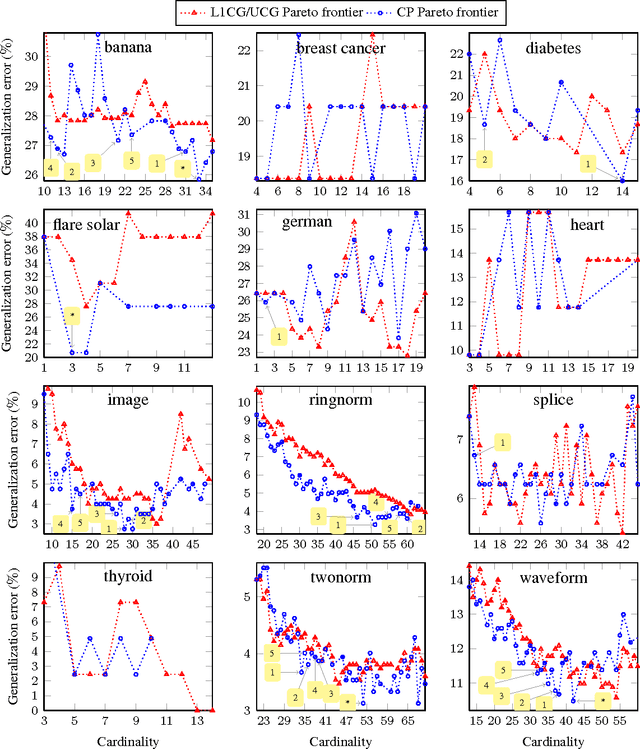
We propose a totally corrective boosting algorithm with explicit cardinality regularization. The resulting combinatorial optimization problems are not known to be efficiently solvable with existing classical methods, but emerging quantum optimization technology gives hope for achieving sparser models in practice. In order to demonstrate the utility of our algorithm, we use a distributed classical heuristic optimizer as a stand-in for quantum hardware. Even though this evaluation methodology incurs large time and resource costs on classical computing machinery, it allows us to gauge the potential gains in generalization performance and sparsity of the resulting boosted ensembles. Our experimental results on public data sets commonly used for benchmarking of boosting algorithms decidedly demonstrate the existence of such advantages. If actual quantum optimization were to be used with this algorithm in the future, we would expect equivalent or superior results at much smaller time and energy costs during training. Moreover, studying cardinality-penalized boosting also sheds light on why unregularized boosting algorithms with early stopping often yield better results than their counterparts with explicit convex regularization: Early stopping performs suboptimal cardinality regularization. The results that we present here indicate it is beneficial to explicitly solve the combinatorial problem still left open at early termination.

Construction of non-convex polynomial loss functions for training a binary classifier with quantum annealing

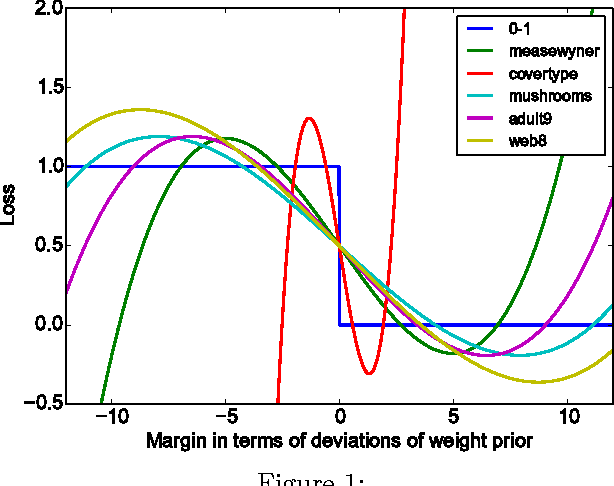
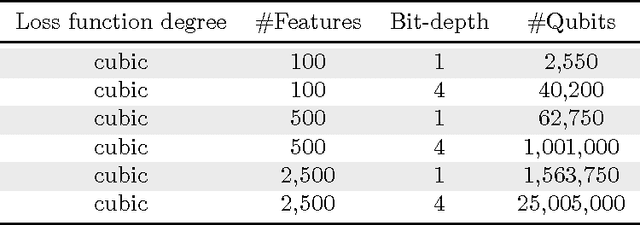
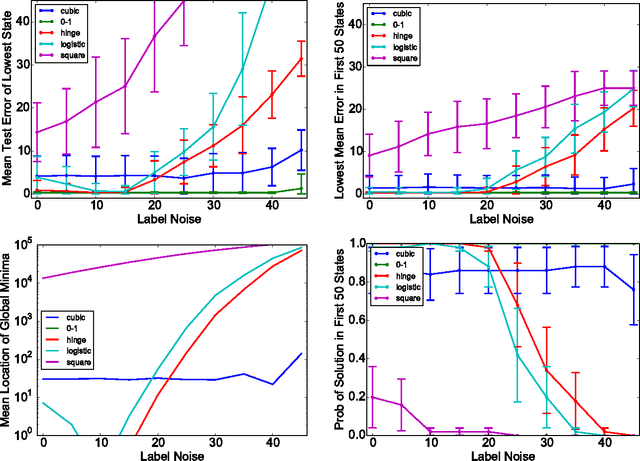
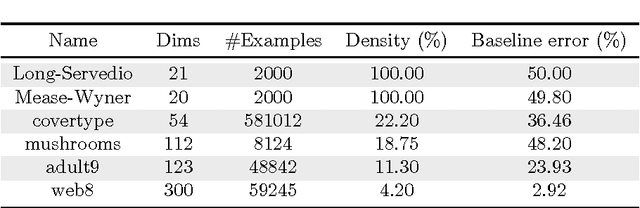
Quantum annealing is a heuristic quantum algorithm which exploits quantum resources to minimize an objective function embedded as the energy levels of a programmable physical system. To take advantage of a potential quantum advantage, one needs to be able to map the problem of interest to the native hardware with reasonably low overhead. Because experimental considerations constrain our objective function to take the form of a low degree PUBO (polynomial unconstrained binary optimization), we employ non-convex loss functions which are polynomial functions of the margin. We show that these loss functions are robust to label noise and provide a clear advantage over convex methods. These loss functions may also be useful for classical approaches as they compile to regularized risk expressions which can be evaluated in constant time with respect to the number of training examples.

Dependent Hierarchical Normalized Random Measures for Dynamic Topic Modeling

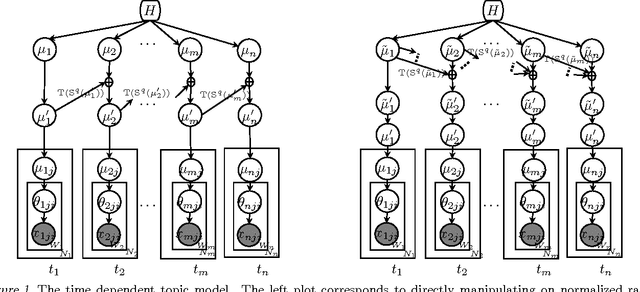
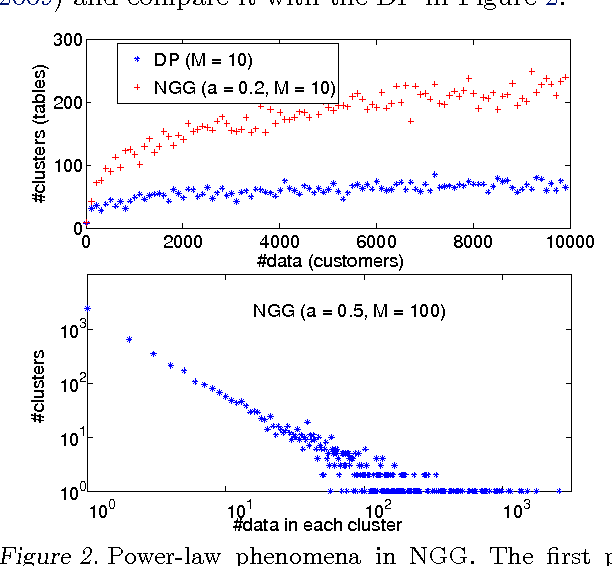
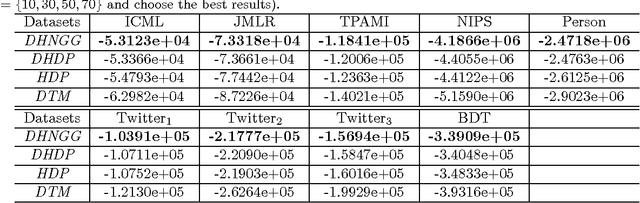
We develop dependent hierarchical normalized random measures and apply them to dynamic topic modeling. The dependency arises via superposition, subsampling and point transition on the underlying Poisson processes of these measures. The measures used include normalised generalised Gamma processes that demonstrate power law properties, unlike Dirichlet processes used previously in dynamic topic modeling. Inference for the model includes adapting a recently developed slice sampler to directly manipulate the underlying Poisson process. Experiments performed on news, blogs, academic and Twitter collections demonstrate the technique gives superior perplexity over a number of previous models.

Theory of Dependent Hierarchical Normalized Random Measures

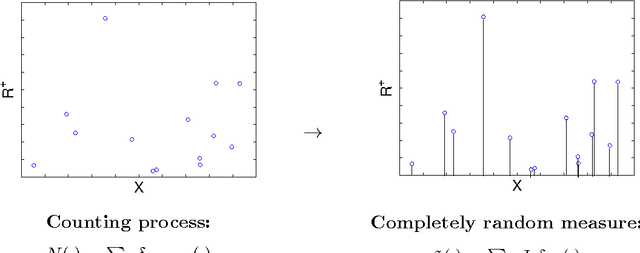
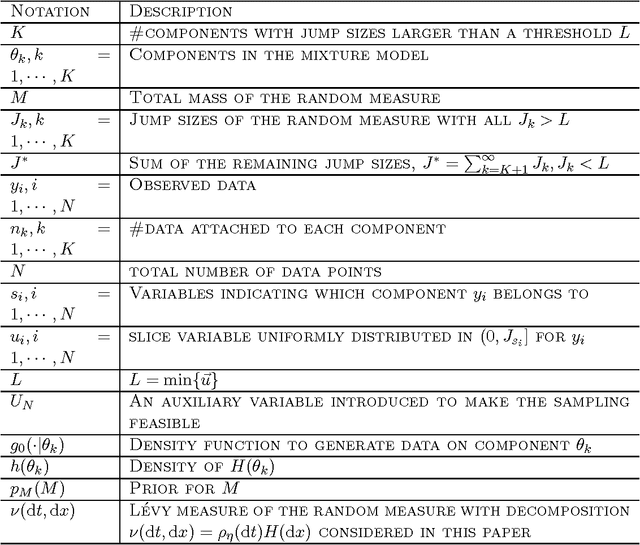
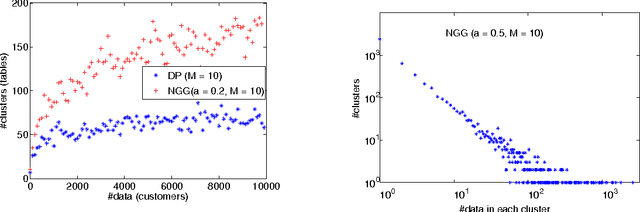
This paper presents theory for Normalized Random Measures (NRMs), Normalized Generalized Gammas (NGGs), a particular kind of NRM, and Dependent Hierarchical NRMs which allow networks of dependent NRMs to be analysed. These have been used, for instance, for time-dependent topic modelling. In this paper, we first introduce some mathematical background of completely random measures (CRMs) and their construction from Poisson processes, and then introduce NRMs and NGGs. Slice sampling is also introduced for posterior inference. The dependency operators in Poisson processes and for the corresponding CRMs and NRMs is then introduced and Posterior inference for the NGG presented. Finally, we give dependency and composition results when applying these operators to NRMs so they can be used in a network with hierarchical and dependent relations.