A model selection approach for clustering a multinomial sequence with non-negative factorization

We consider a problem of clustering a sequence of multinomial observations by way of a model selection criterion. We propose a form of a penalty term for the model selection procedure. Our approach subsumes both the conventional AIC and BIC criteria but also extends the conventional criteria in a way that it can be applicable also to a sequence of sparse multinomial observations, where even within a same cluster, the number of multinomial trials may be different for different observations. In addition, as a preliminary estimation step to maximum likelihood estimation, and more generally, to maximum $L_{q}$ estimation, we propose to use reduced rank projection in combination with non-negative factorization. We motivate our approach by showing that our model selection criterion and preliminary estimation step yield consistent estimates under simplifying assumptions. We also illustrate our approach through numerical experiments using real and simulated data.

Techniques for clustering interaction data as a collection of graphs

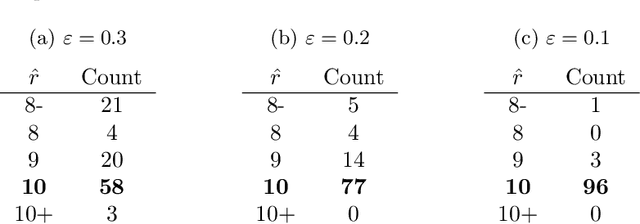
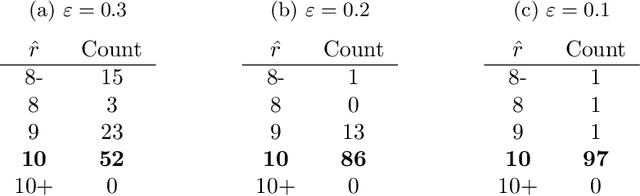
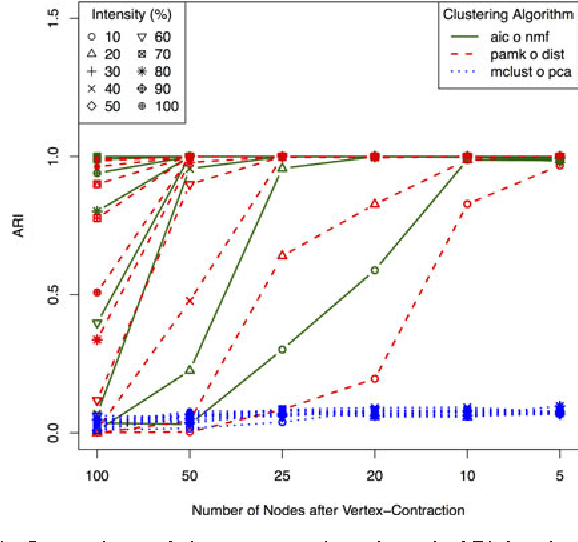
A natural approach to analyze interaction data of form "what-connects-to-what-when" is to create a time-series (or rather a sequence) of graphs through temporal discretization (bandwidth selection) and spatial discretization (vertex contraction). Such discretization together with non-negative factorization techniques can be useful for obtaining clustering of graphs. Motivating application of performing clustering of graphs (as opposed to vertex clustering) can be found in neuroscience and in social network analysis, and it can also be used to enhance community detection (i.e., vertex clustering) by way of conditioning on the cluster labels. In this paper, we formulate a problem of clustering of graphs as a model selection problem. Our approach involves information criteria, non-negative matrix factorization and singular value thresholding, and we illustrate our techniques using real and simulated data.

Automatic Dimension Selection for a Non-negative Factorization Approach to Clustering Multiple Random Graphs

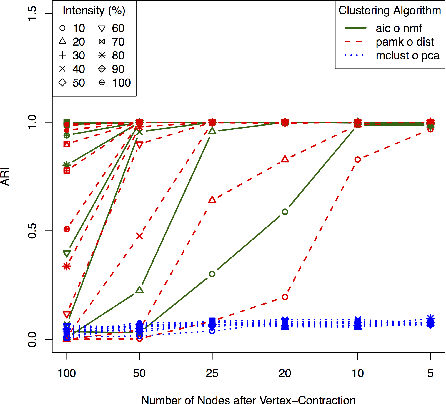
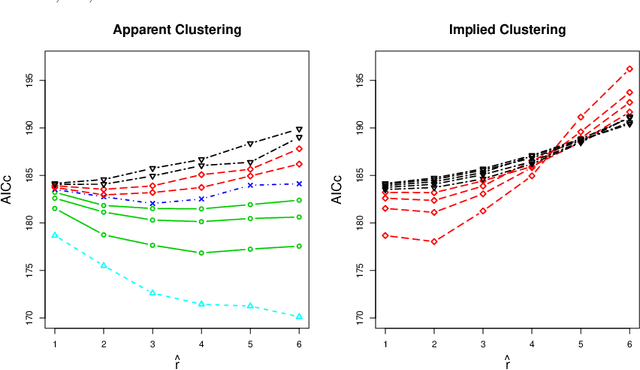
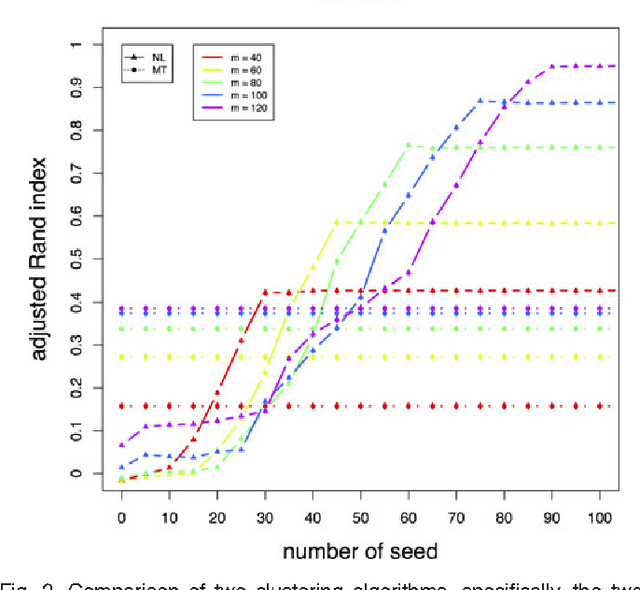
We consider a problem of grouping multiple graphs into several clusters using singular value thesholding and non-negative factorization. We derive a model selection information criterion to estimate the number of clusters. We demonstrate our approach using "Swimmer data set" as well as simulated data set, and compare its performance with two standard clustering algorithms.

On latent position inference from doubly stochastic messaging activities

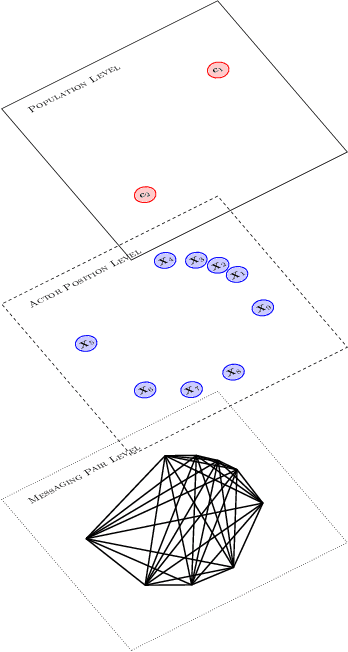
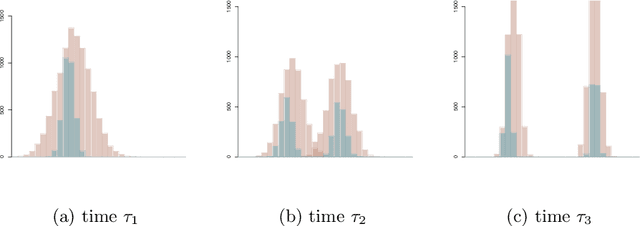
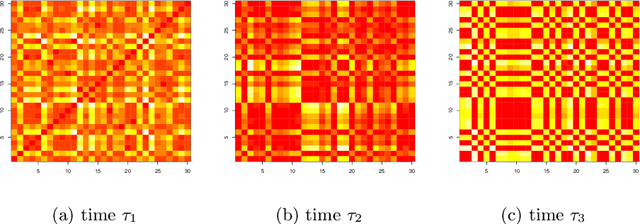
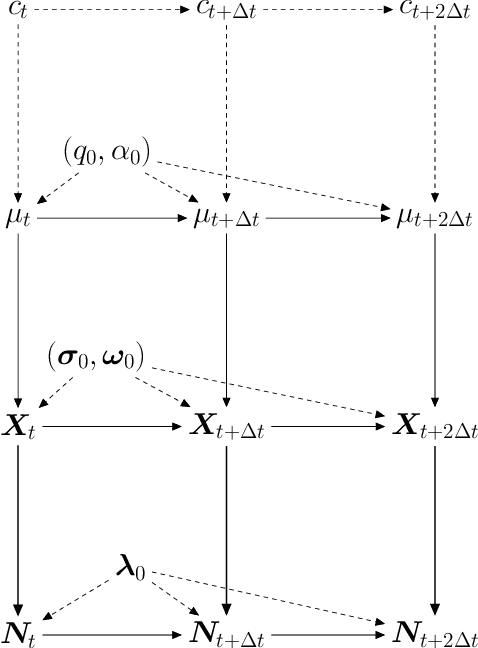
We model messaging activities as a hierarchical doubly stochastic point process with three main levels, and develop an iterative algorithm for inferring actors' relative latent positions from a stream of messaging activity data. Each of the message-exchanging actors is modeled as a process in a latent space. The actors' latent positions are assumed to be influenced by the distribution of a much larger population over the latent space. Each actor's movement in the latent space is modeled as being governed by two parameters that we call confidence and visibility, in addition to dependence on the population distribution. The messaging frequency between a pair of actors is assumed to be inversely proportional to the distance between their latent positions. Our inference algorithm is based on a projection approach to an online filtering problem. The algorithm associates each actor with a probability density-valued process, and each probability density is assumed to be a mixture of basis functions. For efficient numerical experiments, we further develop our algorithm for the case where the basis functions are obtained by translating and scaling a standard Gaussian density.