A Catalyst Framework for the Quantum Linear System Problem via the Proximal Point Algorithm

Solving systems of linear equations is a fundamental problem, but it can be computationally intensive for classical algorithms in high dimensions. Existing quantum algorithms can achieve exponential speedups for the quantum linear system problem (QLSP) in terms of the problem dimension, but even such a theoretical advantage is bottlenecked by the condition number of the coefficient matrix. In this work, we propose a new quantum algorithm for QLSP inspired by the classical proximal point algorithm (PPA). Our proposed method can be viewed as a meta-algorithm that allows inverting a modified matrix via an existing \texttt{QLSP\_solver}, thereby directly approximating the solution vector instead of approximating the inverse of the coefficient matrix. By carefully choosing the step size $\eta$, the proposed algorithm can effectively precondition the linear system to mitigate the dependence on condition numbers that hindered the applicability of previous approaches.

Sampling-based sublinear low-rank matrix arithmetic framework for dequantizing quantum machine learning

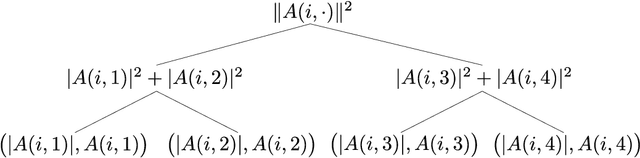
We present an algorithmic framework generalizing quantum-inspired polylogarithmic-time algorithms on low-rank matrices. Our work follows the line of research started by Tang's breakthrough classical algorithm for recommendation systems [STOC'19]. The main result of this work is an algorithm for singular value transformation on low-rank inputs in the quantum-inspired regime, where singular value transformation is a framework proposed by Gily\'en et al. [STOC'19] to study various quantum speedups. Since singular value transformation encompasses a vast range of matrix arithmetic, this result, combined with simple sampling lemmas from previous work, suffices to generalize all results dequantizing quantum machine learning algorithms to the authors' knowledge. Via simple black-box applications of our singular value transformation framework, we recover the dequantization results on recommendation systems, principal component analysis, supervised clustering, low-rank matrix inversion, low-rank semidefinite programming, and support vector machines. We also give additional dequantizations results on low-rank Hamiltonian simulation and discriminant analysis.

Quantum-inspired classical sublinear-time algorithm for solving low-rank semidefinite programming via sampling approaches

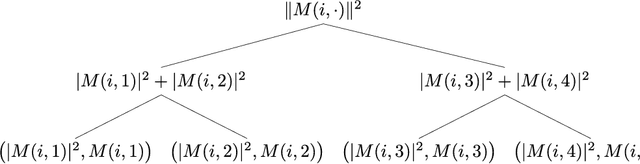
Semidefinite programming (SDP) is a central topic in mathematical optimization with extensive studies on its efficient solvers. Recently, quantum algorithms with superpolynomial speedups for solving SDPs have been proposed assuming access to its constraint matrices in quantum superposition. Mutually inspired by both classical and quantum SDP solvers, in this paper we present a sublinear classical algorithm for solving low-rank SDPs which is asymptotically as good as existing quantum algorithms. Specifically, given an SDP with $m$ constraint matrices, each of dimension $n$ and rank $\mathrm{poly}(\log n)$, our algorithm gives a succinct description and any entry of the solution matrix in time $O(m\cdot\mathrm{poly}(\log n,1/\varepsilon))$ given access to a sample-based low-overhead data structure of the constraint matrices, where $\varepsilon$ is the precision of the solution. In addition, we apply our algorithm to a quantum state learning task as an application. Technically, our approach aligns with both the SDP solvers based on the matrix multiplicative weight (MMW) framework and the recent studies of quantum-inspired machine learning algorithms. The cost of solving SDPs by MMW mainly comes from the exponentiation of Hermitian matrices, and we propose two new technical ingredients (compared to previous sample-based algorithms) for this task that may be of independent interest: $\bullet$ Weighted sampling: assuming sampling access to each individual constraint matrix $A_{1},\ldots,A_{\tau}$, we propose a procedure that gives a good approximation of $A=A_{1}+\cdots+A_{\tau}$. $\bullet$ Symmetric approximation: we propose a sampling procedure that gives low-rank spectral decomposition of a Hermitian matrix $A$. This improves upon previous sampling procedures that only give low-rank singular value decompositions, losing the signs of eigenvalues.

Quantum-inspired sublinear classical algorithms for solving low-rank linear systems

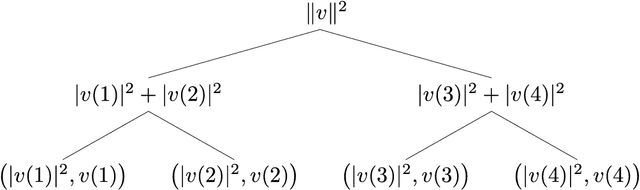
We present classical sublinear-time algorithms for solving low-rank linear systems of equations. Our algorithms are inspired by the HHL quantum algorithm for solving linear systems and the recent breakthrough by Tang of dequantizing the quantum algorithm for recommendation systems. Let $A \in \mathbb{C}^{m \times n}$ be a rank-$k$ matrix, and $b \in \mathbb{C}^m$ be a vector. We present two algorithms: a "sampling" algorithm that provides a sample from $A^{-1}b$ and a "query" algorithm that outputs an estimate of an entry of $A^{-1}b$, where $A^{-1}$ denotes the Moore-Penrose pseudo-inverse. Both of our algorithms have query and time complexity $O(\mathrm{poly}(k, \kappa, \|A\|_F, 1/\epsilon)\,\mathrm{polylog}(m, n))$, where $\kappa$ is the condition number of $A$ and $\epsilon$ is the precision parameter. Note that the algorithms we consider are sublinear time, so they cannot write and read the whole matrix or vectors. In this paper, we assume that $A$ and $b$ come with well-known low-overhead data structures such that entries of $A$ and $b$ can be sampled according to some natural probability distributions. Alternatively, when $A$ is positive semidefinite, our algorithms can be adapted so that the sampling assumption on $b$ is not required.