Combined Compromise for Ideal Solution (CoCoFISo): a multi-criteria decision-making based on the CoCoSo method algorithm

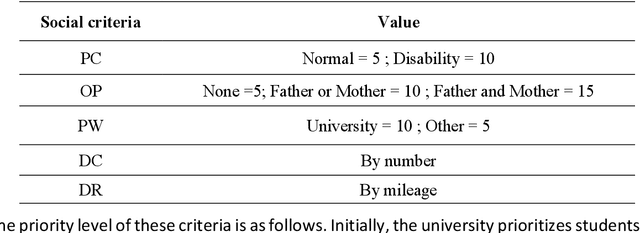
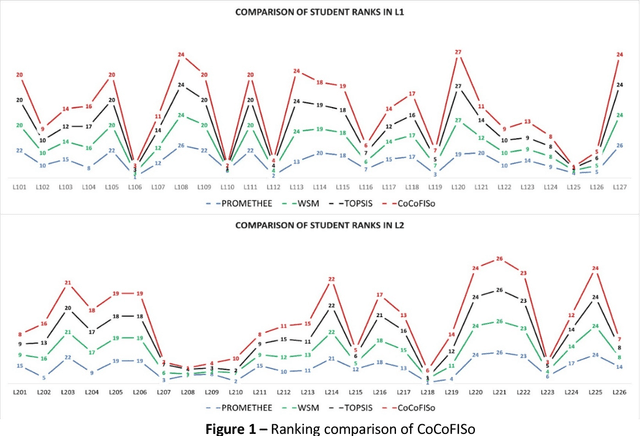
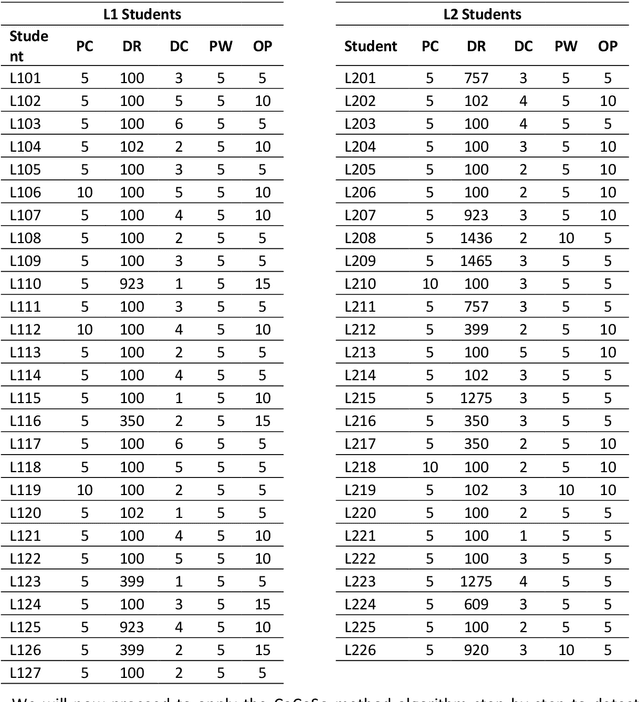
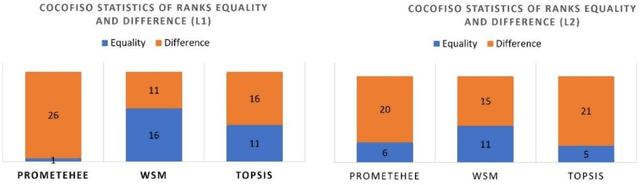
Each decision-making tool should be tested and validated in real case studies to be practical and fit to global problems. The application of multi-criteria decision-making methods (MCDM) is currently a trend to rank alternatives. In the literature, there are several multi-criteria decision-making methods according to their classification. During our experimentation on the Combined Compromise Solution (CoCoSo) method, we encountered its limits for real cases. The authors examined the applicability of the CoCoFISo method (improved version of combined compromise solution), by a real case study in a university campus and compared the obtained results to other MCDMs such as Preference Ranking Organisation Method for Enrichment Evaluations (PROMETHEE), Weighted Sum Method (WSM) and Technique for Order Preference by Similarity to the Ideal Solution (TOPSIS). Our research finding indicates that CoCoSo is an applied method that has been developed to solve complex multi variable assessment problems, while CoCoFISo can improve the shortages observed in CoCoSo and deliver stable outcomes compared to other developed tools. The findings imply that application of CoCoFISo is suggested to decision makers, experts and researchers while they are facing practical challenges and sensitive questions regarding the utilization of a reliable decision-making method. Unlike many prior studies, the current version of CoCoSo is unique, original and is presented for the first time. Its performance was approved using several strategies and examinations.

A VIKOR and TOPSIS focused reanalysis of the MADM methods based on logarithmic normalization

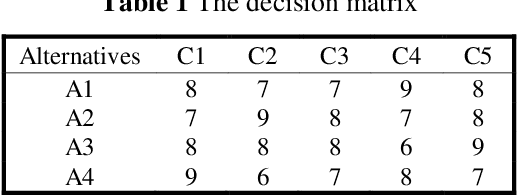
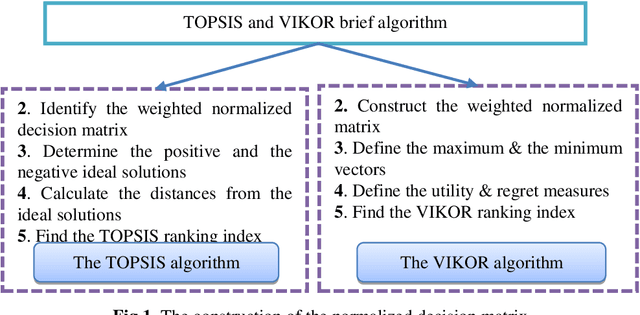
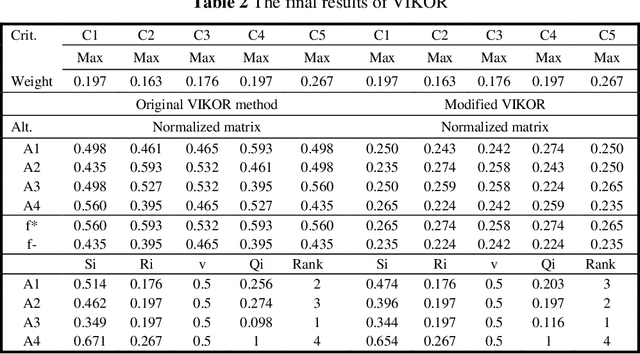
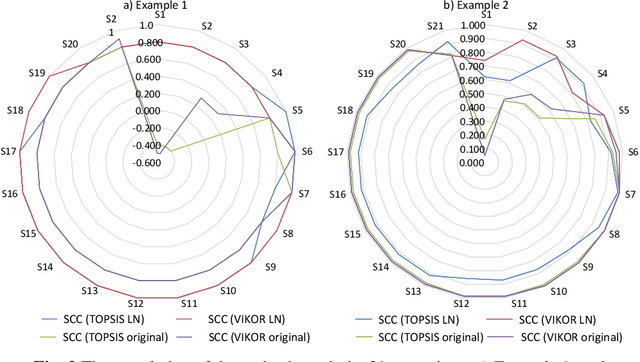
Decision and policy-makers in multi-criteria decision-making analysis take into account some strategies in order to analyze outcomes and to finally make an effective and more precise decision. Among those strategies, the modification of the normalization process in the multiple-criteria decision-making algorithm is still a question due to the confrontation of many normalization tools. Normalization is the basic action in defining and solving a MADM problem and a MADM model. Normalization is the first, also necessary, step in solving, i.e. the application of a MADM method. It is a fact that the selection of normalization methods has a direct effect on the results. One of the latest normalization methods introduced is the Logarithmic Normalization (LN) method. This new method has a distinguished advantage, reflecting in that a sum of the normalized values of criteria always equals 1. This normalization method had never been applied in any MADM methods before. This research study is focused on the analysis of the classical MADM methods based on logarithmic normalization. VIKOR and TOPSIS, as the two famous MADM methods, were selected for this reanalysis research study. Two numerical examples were checked in both methods, based on both the classical and the novel ways based on the LN. The results indicate that there are differences between the two approaches. Eventually, a sensitivity analysis is also designed to illustrate the reliability of the final results.