Synthetic Time Series Forecasting with Transformer Architectures: Extensive Simulation Benchmarks

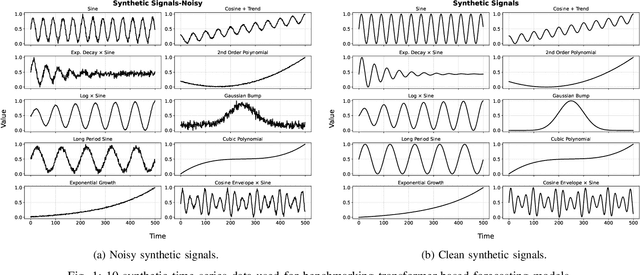
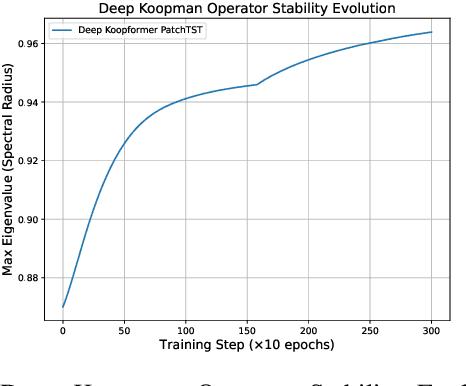
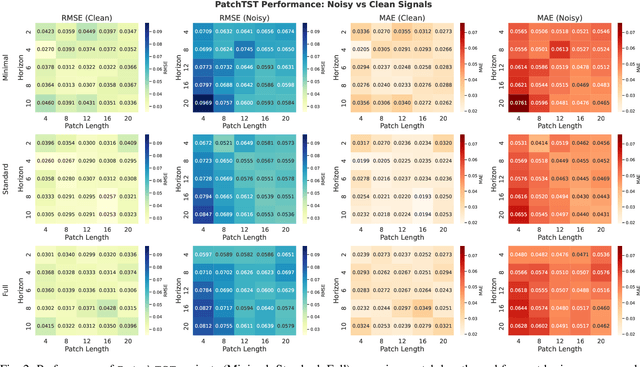
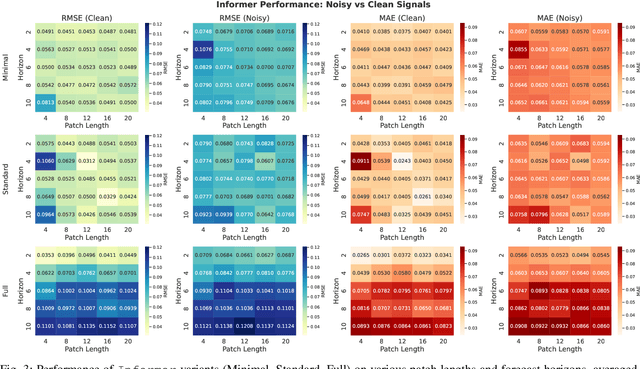
Time series forecasting plays a critical role in domains such as energy, finance, and healthcare, where accurate predictions inform decision-making under uncertainty. Although Transformer-based models have demonstrated success in sequential modeling, their adoption for time series remains limited by challenges such as noise sensitivity, long-range dependencies, and a lack of inductive bias for temporal structure. In this work, we present a unified and principled framework for benchmarking three prominent Transformer forecasting architectures-Autoformer, Informer, and Patchtst-each evaluated through three architectural variants: Minimal, Standard, and Full, representing increasing levels of complexity and modeling capacity. We conduct over 1500 controlled experiments on a suite of ten synthetic signals, spanning five patch lengths and five forecast horizons under both clean and noisy conditions. Our analysis reveals consistent patterns across model families. To advance this landscape further, we introduce the Koopman-enhanced Transformer framework, Deep Koopformer, which integrates operator-theoretic latent state modeling to improve stability and interpretability. We demonstrate its efficacy on nonlinear and chaotic dynamical systems. Our results highlight Koopman based Transformer as a promising hybrid approach for robust, interpretable, and theoretically grounded time series forecasting in noisy and complex real-world conditions.

Probabilistic Formulations for System Identification of Linear Dynamics with Bilinear Observation Models

In this paper, we address the identification problem for the systems characterized by linear time-invariant dynamics with bilinear observation models. More precisely, we consider a suitable parametric description of the system and formulate the identification problem as the estimation of the parameters defining the mathematical model of the system using the observed input-output data. To this end, we propose two probabilistic frameworks. The first framework employs the Maximum Likelihood (ML) approach, which accurately finds the optimal parameter estimates by maximizing a likelihood function. Subsequently, we develop a tractable first-order method to solve the optimization problem corresponding to the proposed ML approach. Additionally, to further improve tractability and computational efficiency of the estimation of the parameters, we introduce an alternative framework based on the Expectation--Maximization (EM) approach, which estimates the parameters using an appropriately designed cost function. We show that the EM cost function is invex, which ensures the existence and uniqueness of the optimal solution. Furthermore, we derive the closed-form solution for the optimal parameters and also prove the recursive feasibility of the EM procedure. Through extensive numerical experiments, the practical implementation of the proposed approaches is demonstrated, and their estimation efficacy is verified and compared, highlighting the effectiveness of the methods to accurately estimate the system parameters and their potential for real-world applications in scenarios involving bilinear observation structures.

Representer Theorem for Learning Koopman Operators

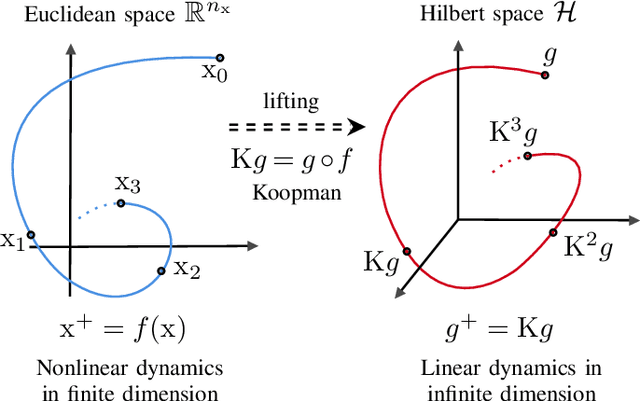
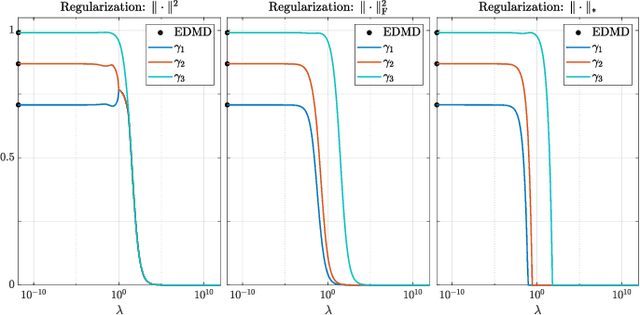
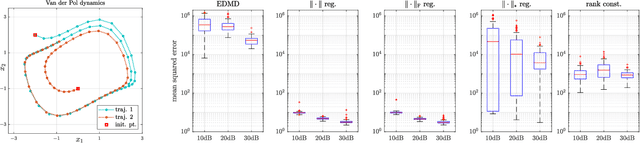
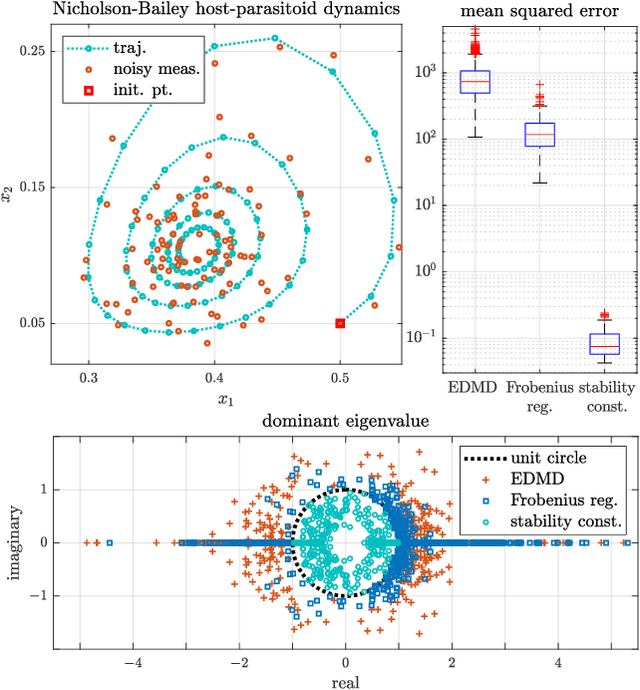
In this work, the problem of learning Koopman operator of a discrete-time autonomous system is considered. The learning problem is formulated as a constrained regularized empirical loss minimization in the infinite-dimensional space of linear operators. We show that under certain but general conditions, a representer theorem holds for the learning problem. This allows reformulating the problem in a finite-dimensional space without any approximation and loss of precision. Following this, we consider various cases of regularization and constraints in the learning problem, including the operator norm, the Frobenius norm, rank, nuclear norm, and stability. Subsequently, we derive the corresponding finite-dimensional problem. Furthermore, we discuss the connection between the proposed formulation and the extended dynamic mode decomposition. Finally, we provide an illustrative numerical example.

The Existence and Uniqueness of Solutions for Kernel-Based System Identification

The notion of reproducing kernel Hilbert space (RKHS) has emerged in system identification during the past decade. In the resulting framework, the impulse response estimation problem is formulated as a regularized optimization defined on an infinite-dimensional RKHS consisting of stable impulse responses. The consequent estimation problem is well-defined under the central assumption that the convolution operators restricted to the RKHS are continuous linear functionals. Moreover, according to this assumption, the representer theorem hold, and therefore, the impulse response can be estimated by solving a finite-dimensional program. Thus, the continuity feature plays a significant role in kernel-based system identification. This paper shows that this central assumption is guaranteed to be satisfied in considerably general situations, namely when the kernel is an integrable function and the input signal is bounded. Furthermore, the strong convexity of the optimization problem and the continuity property of the convolution operators imply that the kernel-based system identification admits a unique solution. Consequently, it follows that kernel-based system identification is a well-defined approach.

Kernel-Based Identification with Frequency Domain Side-Information

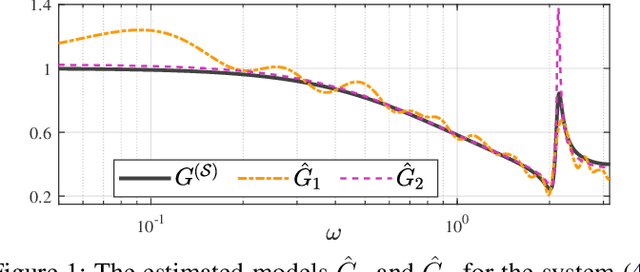
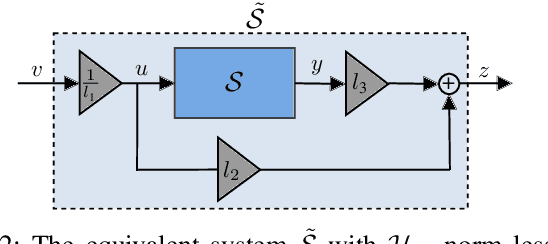
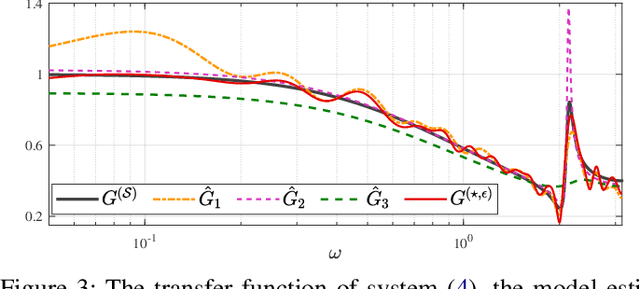
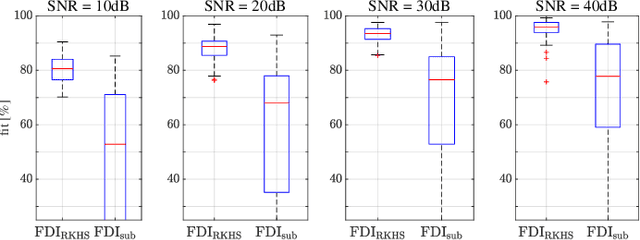
This paper discusses the problem of system identification when frequency domain side-information is available. Initially, we consider the case where the side-information is provided as the $\mathcal{H}_{\infty}$-norm of the system being bounded by a given scalar. This framework allows considering different forms of frequency domain side-information, such as the dissipativity of the system. We propose a nonparametric identification approach for estimating the impulse response of the system under the given side-information. The estimation problem is formulated as a constrained optimization in a stable reproducing kernel Hilbert space, where suitable constraints are considered for incorporating the desired frequency domain features. The resulting optimization has an infinite-dimensional feasible set with an infinite number of constraints. We show that this problem is a well-defined convex program with a unique solution. We propose a heuristic that tightly approximates this unique solution. The proposed approach is equivalent to solving a finite-dimensional convex quadratically constrained quadratic program. The efficiency of the discussed method is verified by several numerical examples.

Distributed Model Predictive Control of Buildings and Energy Hubs

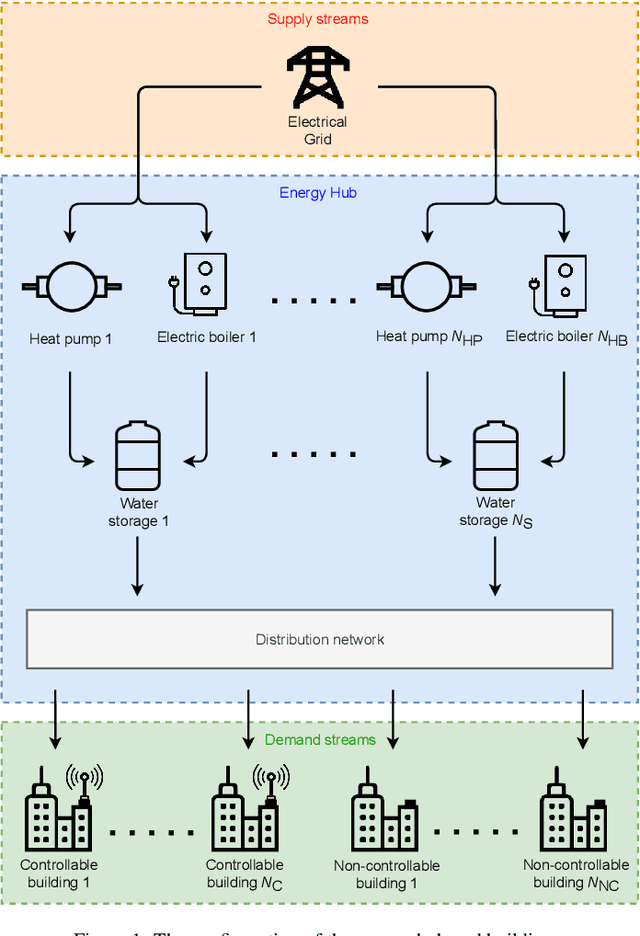
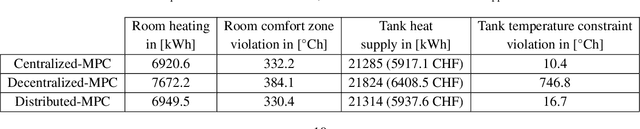
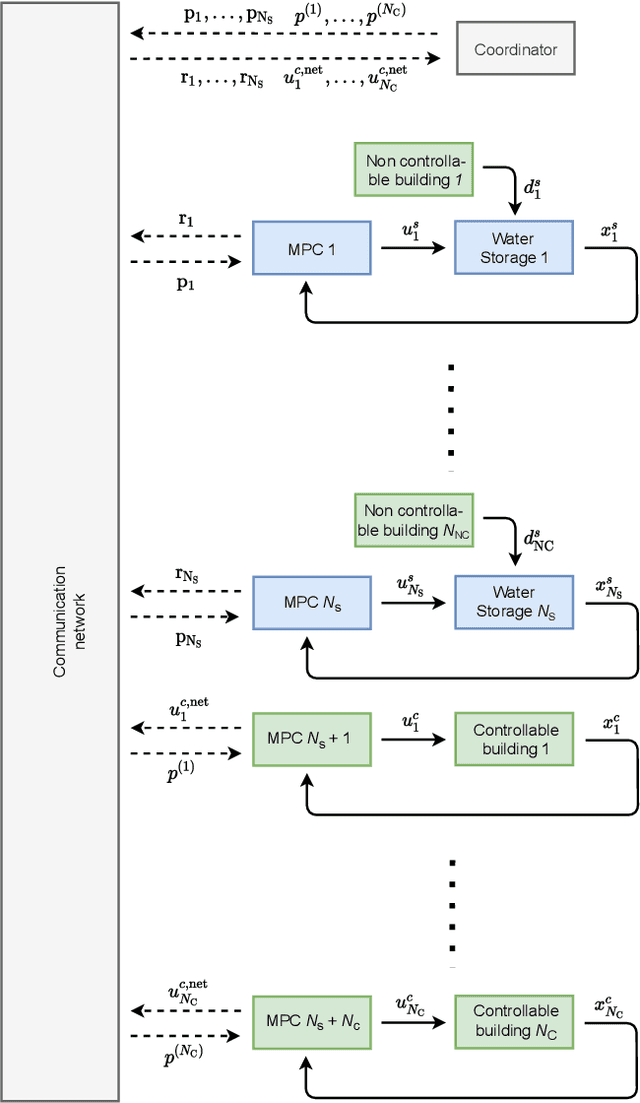
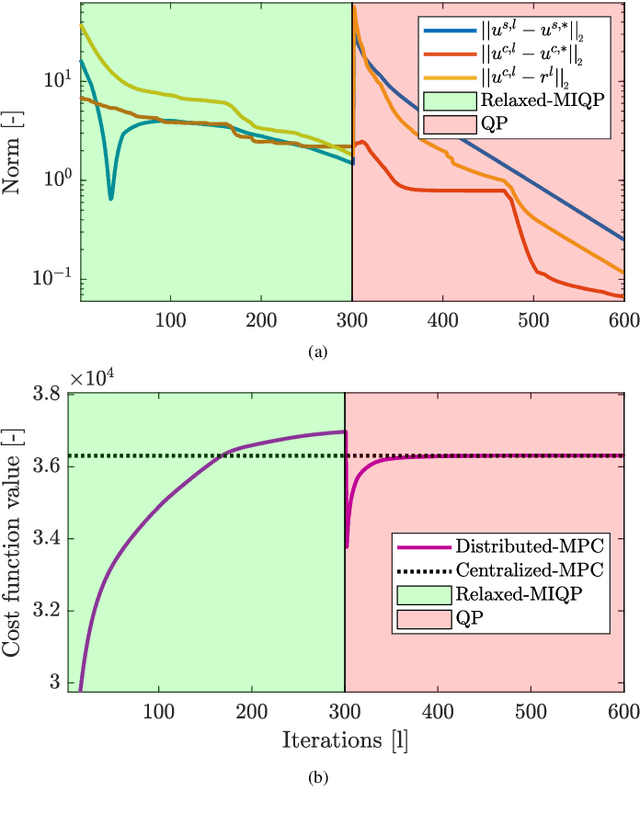
Model predictive control (MPC) strategies can be applied to the coordination of energy hubs to reduce their energy consumption. Despite the effectiveness of these techniques, their potential for energy savings are potentially underutilized due to the fact that energy demands are often assumed to be fixed quantities rather than controlled dynamic variables. The joint optimization of energy hubs and buildings' energy management systems can result in higher energy savings. This paper investigates how different MPC strategies perform on energy management systems in buildings and energy hubs. We first discuss two MPC approaches; centralized and decentralized. While the centralized control strategy offers optimal performance, its implementation is computationally prohibitive and raises privacy concerns. On the other hand, the decentralized control approach, which offers ease of implementation, displays significantly lower performance. We propose a third strategy, distributed control based on dual decomposition, which has the advantages of both approaches. Numerical case studies and comparisons demonstrate that the performance of distributed control is close to the performance of the centralized case, while maintaining a significantly lower computational burden, especially in large-scale scenarios with many agents. Finally, we validate and verify the reliability of the proposed method through an experiment on a full-scale energy hub system in the NEST demonstrator in D\"{u}bendorf, Switzerland.

On Robustness of Kernel-Based Regularized System Identification

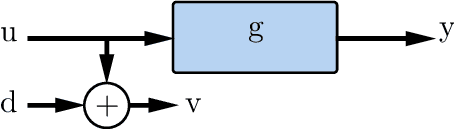
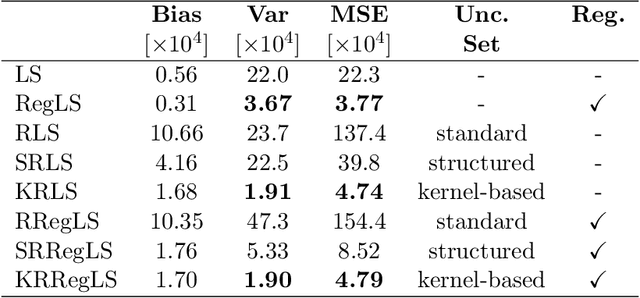
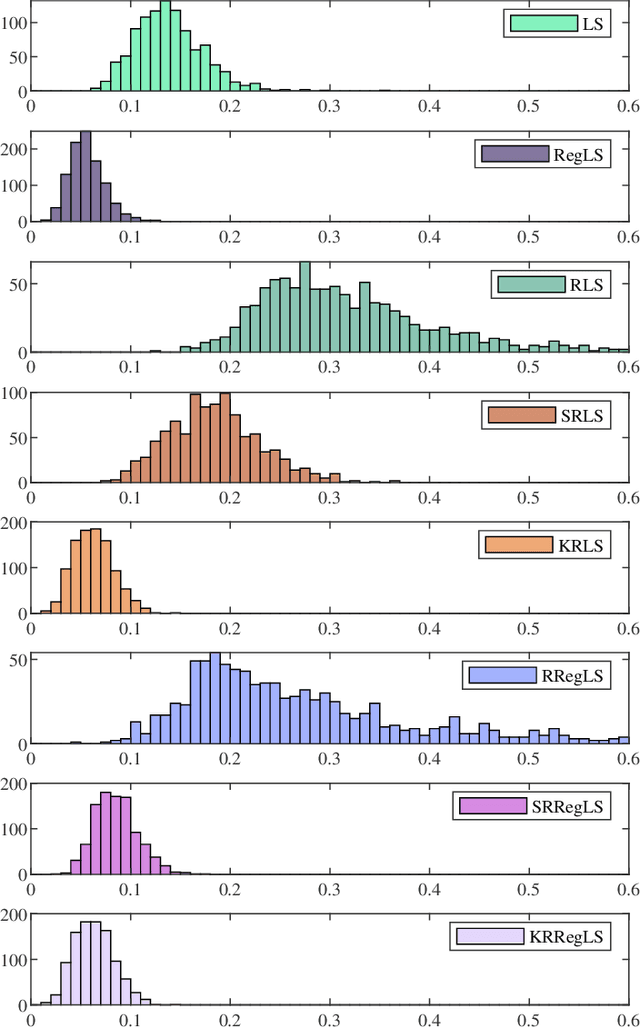
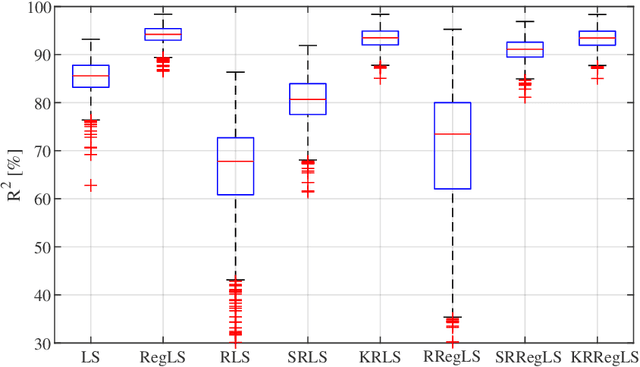
This paper presents a novel feature of the kernel-based system identification method. We prove that the regularized kernel-based approach for the estimation of a finite impulse response is equivalent to a robust least-squares problem with a particular uncertainty set defined in terms of the kernel matrix, and thus, it is called kernel-based uncertainty set. We provide a theoretical foundation for the robustness of the kernel-based approach to input disturbances. Based on robust and regularized least-squares methods, different formulations of system identification are considered, where the kernel-based uncertainty set is employed in some of them. We apply these methods to a case where the input measurements are subject to disturbances. Subsequently, we perform extensive numerical experiments and compare the results to examine the impact of utilizing kernel-based uncertainty sets in the identification procedure. The numerical experiments confirm that the robust least square identification approach with the kernel-based uncertainty set improves the robustness of the estimation to the input disturbances.

Parameter Identification for Digital Fabrication: A Gaussian Process Learning Approach

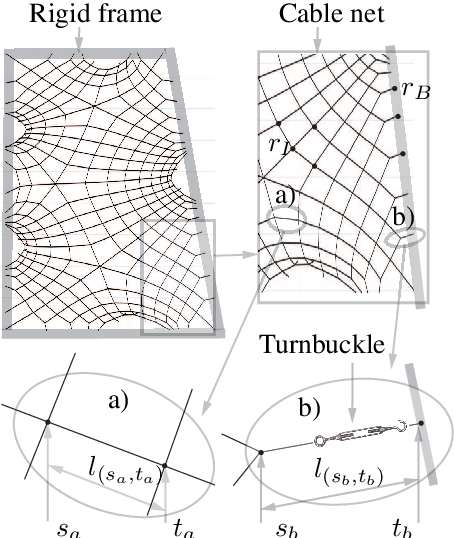
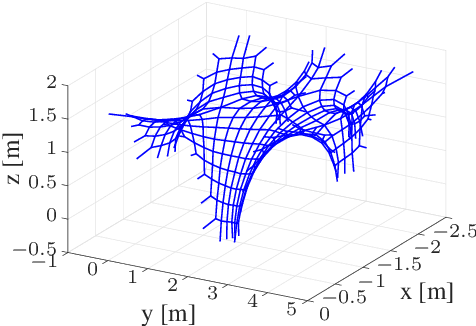
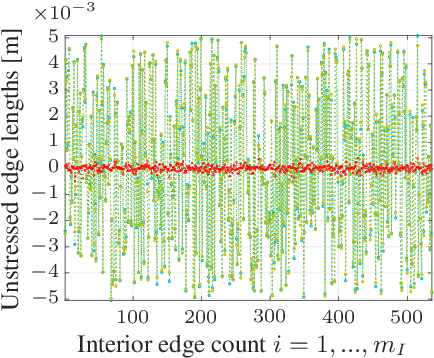
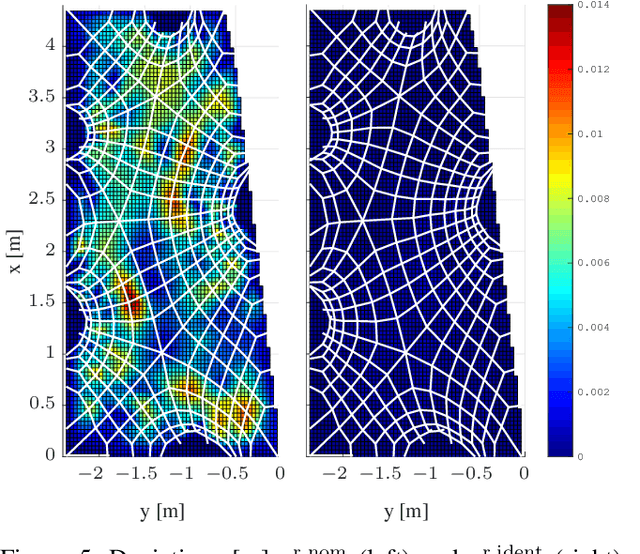
Tensioned cable nets can be used as supporting structures for the efficient construction of lightweight building elements, such as thin concrete shell structures. To guarantee important mechanical properties of the latter, the tolerances on deviations of the tensioned cable net geometry from the desired target form are very tight. Therefore, the form needs to be readjusted on the construction site. In order to employ model-based optimization techniques, the precise identification of important uncertain model parameters of the cable net system is required. This paper proposes the use of Gaussian process regression to learn the function that maps the cable net geometry to the uncertain parameters. In contrast to previously proposed methods, this approach requires only a single form measurement for the identification of the cable net model parameters. This is beneficial since measurements of the cable net form on the construction site are very expensive. For the training of the Gaussian processes, simulated data is efficiently computed via convex programming. The effectiveness of the proposed method and the impact of the precise identification of the parameters on the form of the cable net are demonstrated in numerical experiments on a quarter-scale prototype of a roof structure.