Evaluating Multi-Hop Reasoning in Large Language Models: A Chemistry-Centric Case Study

In this study, we introduced a new benchmark consisting of a curated dataset and a defined evaluation process to assess the compositional reasoning capabilities of large language models within the chemistry domain. We designed and validated a fully automated pipeline, verified by subject matter experts, to facilitate this task. Our approach integrates OpenAI reasoning models with named entity recognition (NER) systems to extract chemical entities from recent literature, which are then augmented with external knowledge bases to form a comprehensive knowledge graph. By generating multi-hop questions across these graphs, we assess LLM performance in both context-augmented and non-context augmented settings. Our experiments reveal that even state-of-the-art models face significant challenges in multi-hop compositional reasoning. The results reflect the importance of augmenting LLMs with document retrieval, which can have a substantial impact on improving their performance. However, even perfect retrieval accuracy with full context does not eliminate reasoning errors, underscoring the complexity of compositional reasoning. This work not only benchmarks and highlights the limitations of current LLMs but also presents a novel data generation pipeline capable of producing challenging reasoning datasets across various domains. Overall, this research advances our understanding of reasoning in computational linguistics.

ChemTEB: Chemical Text Embedding Benchmark, an Overview of Embedding Models Performance & Efficiency on a Specific Domain

Recent advancements in language models have started a new era of superior information retrieval and content generation, with embedding models playing an important role in optimizing data representation efficiency and performance. While benchmarks like the Massive Text Embedding Benchmark (MTEB) have standardized the evaluation of general domain embedding models, a gap remains in specialized fields such as chemistry, which require tailored approaches due to domain-specific challenges. This paper introduces a novel benchmark, the Chemical Text Embedding Benchmark (ChemTEB), designed specifically for the chemical sciences. ChemTEB addresses the unique linguistic and semantic complexities of chemical literature and data, offering a comprehensive suite of tasks on chemical domain data. Through the evaluation of 34 open-source and proprietary models using this benchmark, we illuminate the strengths and weaknesses of current methodologies in processing and understanding chemical information. Our work aims to equip the research community with a standardized, domain-specific evaluation framework, promoting the development of more precise and efficient NLP models for chemistry-related applications. Furthermore, it provides insights into the performance of generic models in a domain-specific context. ChemTEB comes with open-source code and data, contributing further to its accessibility and utility.

MLGCN: An Ultra Efficient Graph Convolution Neural Model For 3D Point Cloud Analysis

The analysis of 3D point clouds has diverse applications in robotics, vision and graphics. Processing them presents specific challenges since they are naturally sparse, can vary in spatial resolution and are typically unordered. Graph-based networks to abstract features have emerged as a promising alternative to convolutional neural networks for their analysis, but these can be computationally heavy as well as memory inefficient. To address these limitations we introduce a novel Multi-level Graph Convolution Neural (MLGCN) model, which uses Graph Neural Networks (GNN) blocks to extract features from 3D point clouds at specific locality levels. Our approach employs precomputed graph KNNs, where each KNN graph is shared between GCN blocks inside a GNN block, making it both efficient and effective compared to present models. We demonstrate the efficacy of our approach on point cloud based object classification and part segmentation tasks on benchmark datasets, showing that it produces comparable results to those of state-of-the-art models while requiring up to a thousand times fewer floating-point operations (FLOPs) and having significantly reduced storage requirements. Thus, our MLGCN model could be particular relevant to point cloud based 3D shape analysis in industrial applications when computing resources are scarce.

Contour Completion using Deep Structural Priors

Humans can easily perceive illusory contours and complete missing forms in fragmented shapes. This work investigates whether such capability can arise in convolutional neural networks (CNNs) using deep structural priors computed directly from images. In this work, we present a framework that completes disconnected contours and connects fragmented lines and curves. In our framework, we propose a model that does not even need to know which regions of the contour are eliminated. We introduce an iterative process that completes an incomplete image and we propose novel measures that guide this to find regions it needs to complete. Our model trains on a single image and fills in the contours with no additional training data. Our work builds a robust framework to achieve contour completion using deep structural priors and extensively investigate how such a model could be implemented.

Medial Spectral Coordinates for 3D Shape Analysis

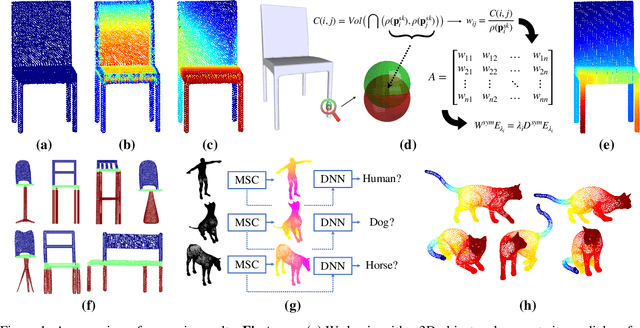
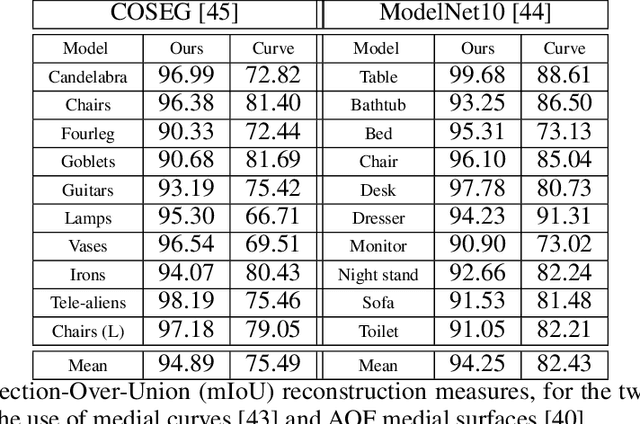
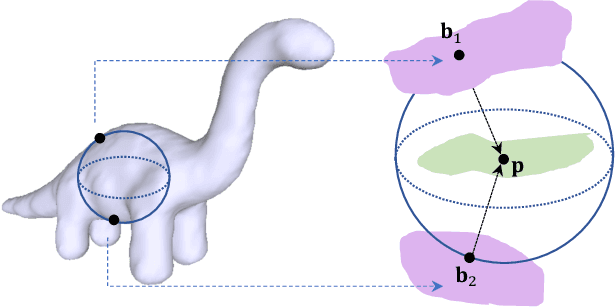
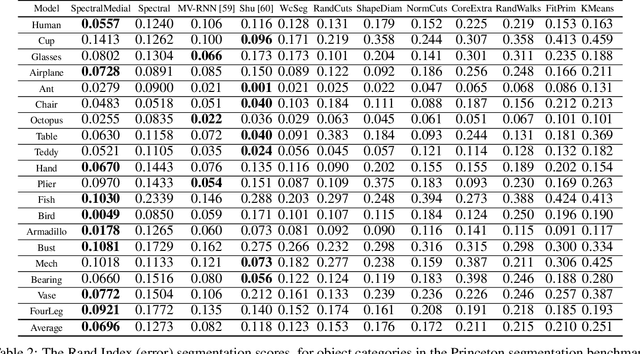
In recent years there has been a resurgence of interest in our community in the shape analysis of 3D objects represented by surface meshes, their voxelized interiors, or surface point clouds. In part, this interest has been stimulated by the increased availability of RGBD cameras, and by applications of computer vision to autonomous driving, medical imaging, and robotics. In these settings, spectral coordinates have shown promise for shape representation due to their ability to incorporate both local and global shape properties in a manner that is qualitatively invariant to isometric transformations. Yet, surprisingly, such coordinates have thus far typically considered only local surface positional or derivative information. In the present article, we propose to equip spectral coordinates with medial (object width) information, so as to enrich them. The key idea is to couple surface points that share a medial ball, via the weights of the adjacency matrix. We develop a spectral feature using this idea, and the algorithms to compute it. The incorporation of object width and medial coupling has direct benefits, as illustrated by our experiments on object classification, object part segmentation, and surface point correspondence.