Exploiting Inferential Structure in Neural Processes

Neural Processes (NPs) are appealing due to their ability to perform fast adaptation based on a context set. This set is encoded by a latent variable, which is often assumed to follow a simple distribution. However, in real-word settings, the context set may be drawn from richer distributions having multiple modes, heavy tails, etc. In this work, we provide a framework that allows NPs' latent variable to be given a rich prior defined by a graphical model. These distributional assumptions directly translate into an appropriate aggregation strategy for the context set. Moreover, we describe a message-passing procedure that still allows for end-to-end optimization with stochastic gradients. We demonstrate the generality of our framework by using mixture and Student-t assumptions that yield improvements in function modelling and test-time robustness.

Memory-Based Dual Gaussian Processes for Sequential Learning

Sequential learning with Gaussian processes (GPs) is challenging when access to past data is limited, for example, in continual and active learning. In such cases, errors can accumulate over time due to inaccuracies in the posterior, hyperparameters, and inducing points, making accurate learning challenging. Here, we present a method to keep all such errors in check using the recently proposed dual sparse variational GP. Our method enables accurate inference for generic likelihoods and improves learning by actively building and updating a memory of past data. We demonstrate its effectiveness in several applications involving Bayesian optimization, active learning, and continual learning.

Variational Bayes Made Easy

Variational Bayes is a popular method for approximate inference but its derivation can be cumbersome. To simplify the process, we give a 3-step recipe to identify the posterior form by explicitly looking for linearity with respect to expectations of well-known distributions. We can then directly write the update by simply ``reading-off'' the terms in front of those expectations. The recipe makes the derivation easier, faster, shorter, and more general.

The Lie-Group Bayesian Learning Rule

The Bayesian Learning Rule provides a framework for generic algorithm design but can be difficult to use for three reasons. First, it requires a specific parameterization of exponential family. Second, it uses gradients which can be difficult to compute. Third, its update may not always stay on the manifold. We address these difficulties by proposing an extension based on Lie-groups where posteriors are parametrized through transformations of an arbitrary base distribution and updated via the group's exponential map. This simplifies all three difficulties for many cases, providing flexible parametrizations through group's action, simple gradient computation through reparameterization, and updates that always stay on the manifold. We use the new learning rule to derive a new algorithm for deep learning with desirable biologically-plausible attributes to learn sparse features. Our work opens a new frontier for the design of new algorithms by exploiting Lie-group structures.

Simplifying Momentum-based Riemannian Submanifold Optimization

Riemannian submanifold optimization with momentum is computationally challenging because ensuring iterates remain on the submanifold often requires solving difficult differential equations. We simplify such optimization algorithms for the submanifold of symmetric positive-definite matrices with the affine invariant metric. We propose a generalized version of the Riemannian normal coordinates which dynamically trivializes the problem into a Euclidean unconstrained problem. We use our approach to explain and simplify existing approaches for structured covariances and develop efficient second-order optimizers for deep learning without explicit matrix inverses.

Can Calibration Improve Sample Prioritization?

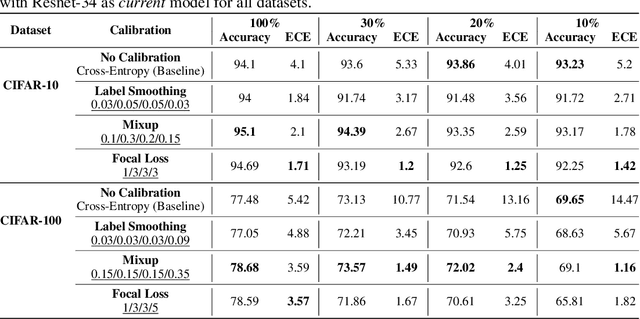
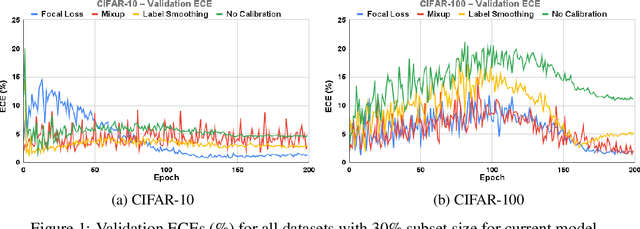
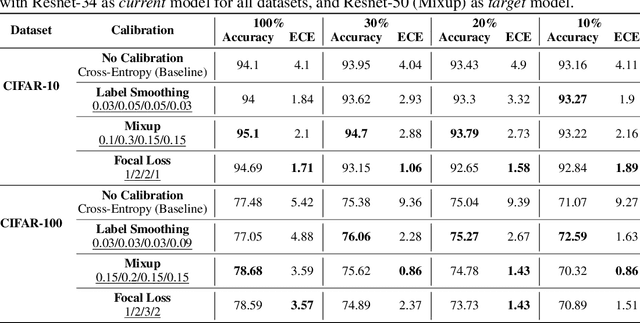
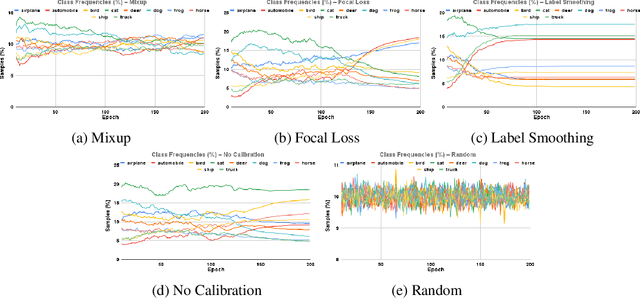
Calibration can reduce overconfident predictions of deep neural networks, but can calibration also accelerate training by selecting the right samples? In this paper, we show that it can. We study the effect of popular calibration techniques in selecting better subsets of samples during training (also called sample prioritization) and observe that calibration can improve the quality of subsets, reduce the number of examples per epoch (by at least 70%), and can thereby speed up the overall training process. We further study the effect of using calibrated pre-trained models coupled with calibration during training to guide sample prioritization, which again seems to improve the quality of samples selected.

SAM as an Optimal Relaxation of Bayes

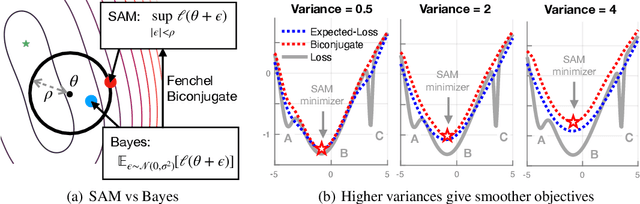
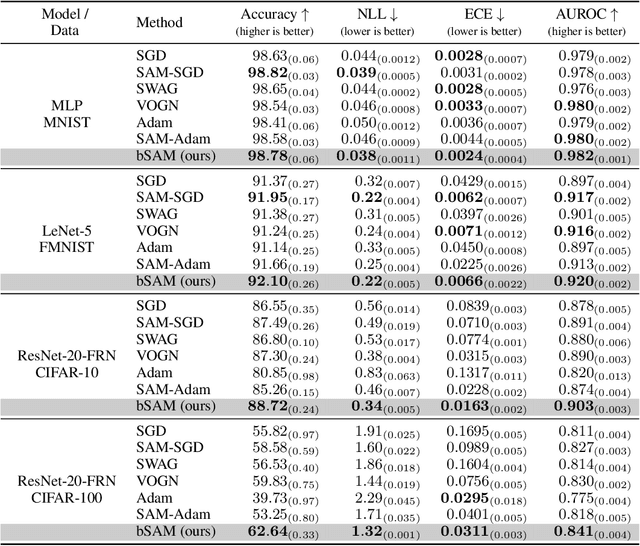
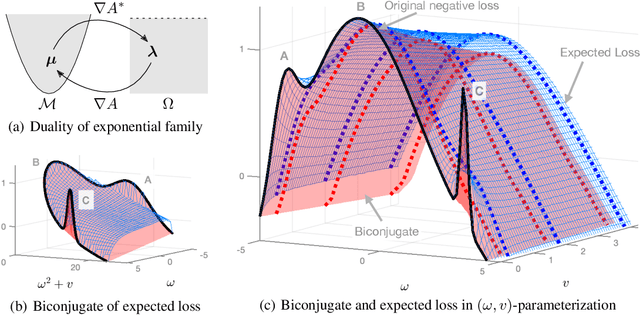
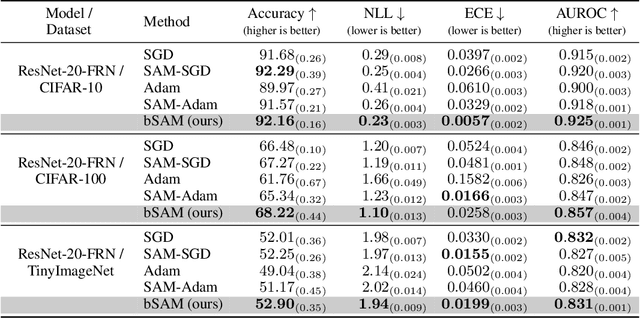
Sharpness-aware minimization (SAM) and related adversarial deep-learning methods can drastically improve generalization, but their underlying mechanisms are not yet fully understood. Here, we establish SAM as a relaxation of the Bayes objective where the expected negative-loss is replaced by the optimal convex lower bound, obtained by using the so-called Fenchel biconjugate. The connection enables a new Adam-like extension of SAM to automatically obtain reasonable uncertainty estimates, while sometimes also improving its accuracy. By connecting adversarial and Bayesian methods, our work opens a new path to robustness.

Dual Parameterization of Sparse Variational Gaussian Processes

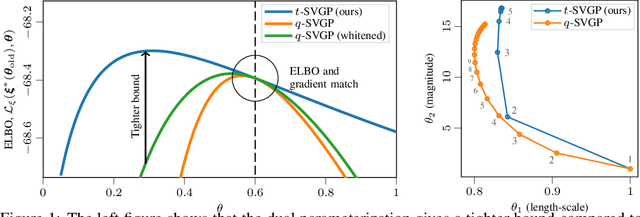
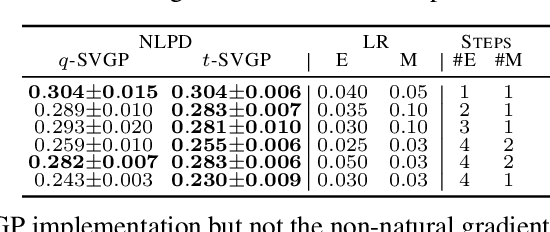
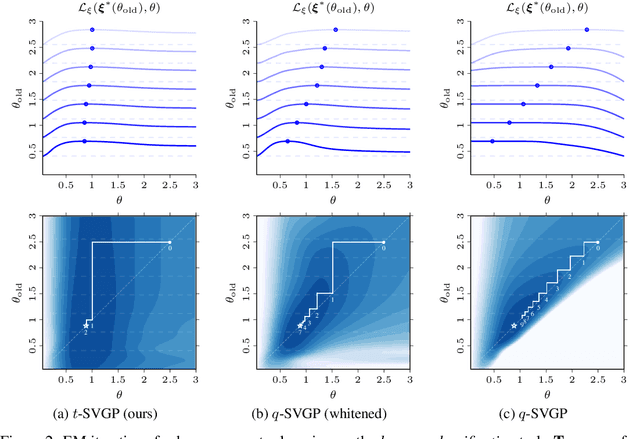
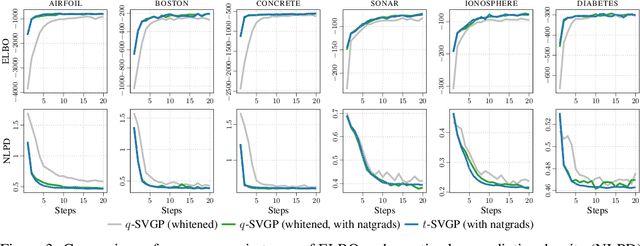
Sparse variational Gaussian process (SVGP) methods are a common choice for non-conjugate Gaussian process inference because of their computational benefits. In this paper, we improve their computational efficiency by using a dual parameterization where each data example is assigned dual parameters, similarly to site parameters used in expectation propagation. Our dual parameterization speeds-up inference using natural gradient descent, and provides a tighter evidence lower bound for hyperparameter learning. The approach has the same memory cost as the current SVGP methods, but it is faster and more accurate.

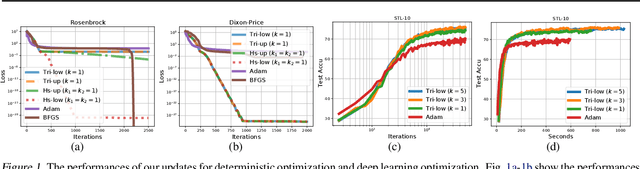
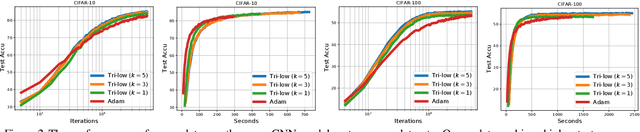
Structured second-order methods via natural gradient descent

In this paper, we propose new structured second-order methods and structured adaptive-gradient methods obtained by performing natural-gradient descent on structured parameter spaces. Natural-gradient descent is an attractive approach to design new algorithms in many settings such as gradient-free, adaptive-gradient, and second-order methods. Our structured methods not only enjoy a structural invariance but also admit a simple expression. Finally, we test the efficiency of our proposed methods on both deterministic non-convex problems and deep learning problems.

Subset-of-Data Variational Inference for Deep Gaussian-Processes Regression

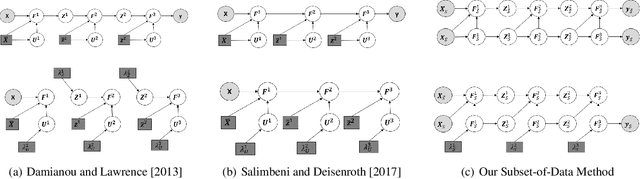
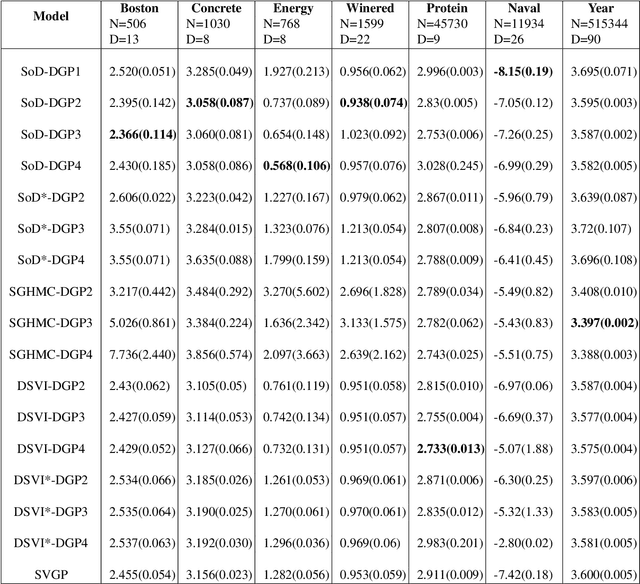
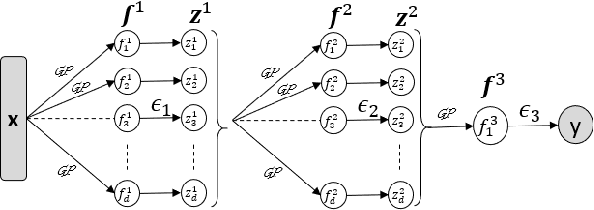
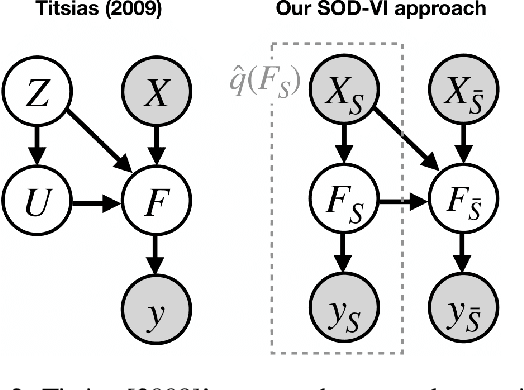
Deep Gaussian Processes (DGPs) are multi-layer, flexible extensions of Gaussian processes but their training remains challenging. Sparse approximations simplify the training but often require optimization over a large number of inducing inputs and their locations across layers. In this paper, we simplify the training by setting the locations to a fixed subset of data and sampling the inducing inputs from a variational distribution. This reduces the trainable parameters and computation cost without significant performance degradations, as demonstrated by our empirical results on regression problems. Our modifications simplify and stabilize DGP training while making it amenable to sampling schemes for setting the inducing inputs.