Refined bounds for randomized experimental design

Experimental design is an approach for selecting samples among a given set so as to obtain the best estimator for a given criterion. In the context of linear regression, several optimal designs have been derived, each associated with a different criterion: mean square error, robustness, \emph{etc}. Computing such designs is generally an NP-hard problem and one can instead rely on a convex relaxation that considers probability distributions over the samples. Although greedy strategies and rounding procedures have received a lot of attention, straightforward sampling from the optimal distribution has hardly been investigated. In this paper, we propose theoretical guarantees for randomized strategies on E and G-optimal design. To this end, we develop a new concentration inequality for the eigenvalues of random matrices using a refined version of the intrinsic dimension that enables us to quantify the performance of such randomized strategies. Finally, we evidence the validity of our analysis through experiments, with particular attention on the G-optimal design applied to the best arm identification problem for linear bandits.

KONG: Kernels for ordered-neighborhood graphs

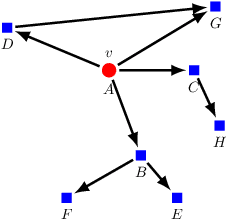
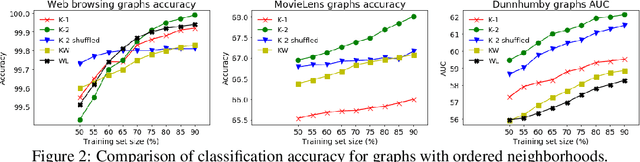
We present novel graph kernels for graphs with node and edge labels that have ordered neighborhoods, i.e. when neighbor nodes follow an order. Graphs with ordered neighborhoods are a natural data representation for evolving graphs where edges are created over time, which induces an order. Combining convolutional subgraph kernels and string kernels, we design new scalable algorithms for generation of explicit graph feature maps using sketching techniques. We obtain precise bounds for the approximation accuracy and computational complexity of the proposed approaches and demonstrate their applicability on real datasets. In particular, our experiments demonstrate that neighborhood ordering results in more informative features. For the special case of general graphs, i.e. graphs without ordered neighborhoods, the new graph kernels yield efficient and simple algorithms for the comparison of label distributions between graphs.

A note on reinforcement learning with Wasserstein distance regularisation, with applications to multipolicy learning

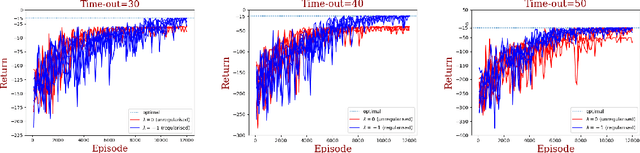
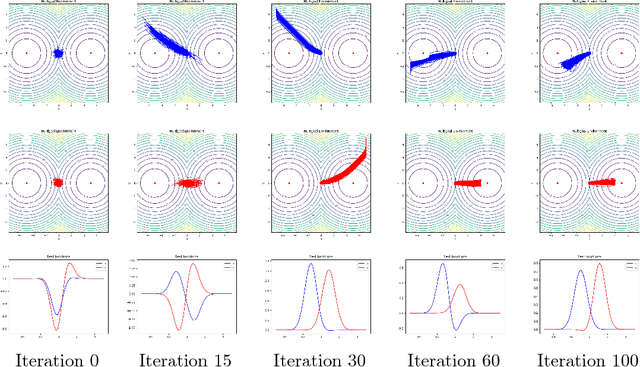
In this note we describe an application of Wasserstein distance to Reinforcement Learning. The Wasserstein distance in question is between the distribution of mappings of trajectories of a policy into some metric space, and some other fixed distribution (which may, for example, come from another policy). Different policies induce different distributions, so given an underlying metric, the Wasserstein distance quantifies how different policies are. This can be used to learn multiple polices which are different in terms of such Wasserstein distances by using a Wasserstein regulariser. Changing the sign of the regularisation parameter, one can learn a policy for which its trajectory mapping distribution is attracted to a given fixed distribution.