CageNet: A Meta-Framework for Learning on Wild Meshes

Learning on triangle meshes has recently proven to be instrumental to a myriad of tasks, from shape classification, to segmentation, to deformation and animation, to mention just a few. While some of these applications are tackled through neural network architectures which are tailored to the application at hand, many others use generic frameworks for triangle meshes where the only customization required is the modification of the input features and the loss function. Our goal in this paper is to broaden the applicability of these generic frameworks to "wild", i.e. meshes in-the-wild which often have multiple components, non-manifold elements, disrupted connectivity, or a combination of these. We propose a configurable meta-framework based on the concept of caged geometry: Given a mesh, a cage is a single component manifold triangle mesh that envelopes it closely. Generalized barycentric coordinates map between functions on the cage, and functions on the mesh, allowing us to learn and test on a variety of data, in different applications. We demonstrate this concept by learning segmentation and skinning weights on difficult data, achieving better performance to state of the art techniques on wild meshes.

SDFs from Unoriented Point Clouds using Neural Variational Heat Distances

We propose a novel variational approach for computing neural Signed Distance Fields (SDF) from unoriented point clouds. To this end, we replace the commonly used eikonal equation with the heat method, carrying over to the neural domain what has long been standard practice for computing distances on discrete surfaces. This yields two convex optimization problems for whose solution we employ neural networks: We first compute a neural approximation of the gradients of the unsigned distance field through a small time step of heat flow with weighted point cloud densities as initial data. Then we use it to compute a neural approximation of the SDF. We prove that the underlying variational problems are well-posed. Through numerical experiments, we demonstrate that our method provides state-of-the-art surface reconstruction and consistent SDF gradients. Furthermore, we show in a proof-of-concept that it is accurate enough for solving a PDE on the zero-level set.

A Differential Geometry Perspective on Orthogonal Recurrent Models

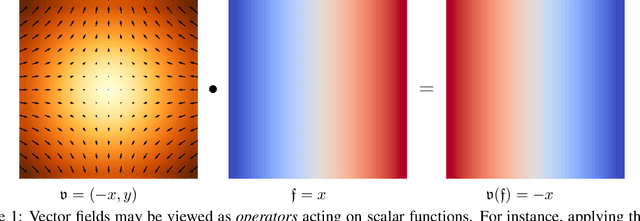
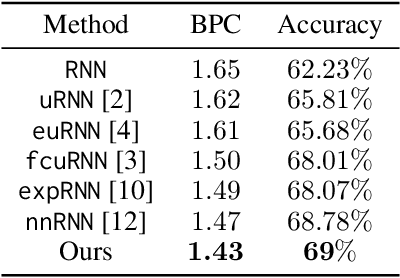
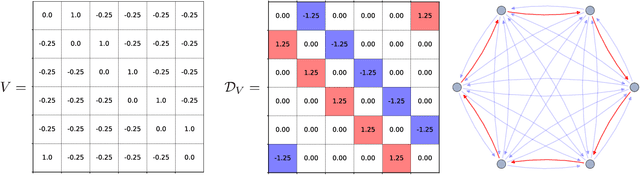
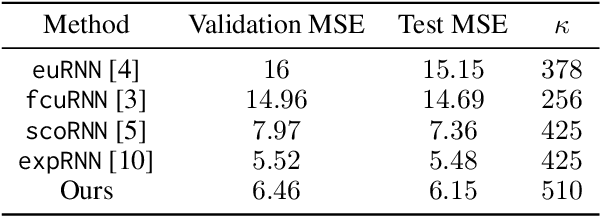
Recently, orthogonal recurrent neural networks (RNNs) have emerged as state-of-the-art models for learning long-term dependencies. This class of models mitigates the exploding and vanishing gradients problem by design. In this work, we employ tools and insights from differential geometry to offer a novel perspective on orthogonal RNNs. We show that orthogonal RNNs may be viewed as optimizing in the space of divergence-free vector fields. Specifically, based on a well-known result in differential geometry that relates vector fields and linear operators, we prove that every divergence-free vector field is related to a skew-symmetric matrix. Motivated by this observation, we study a new recurrent model, which spans the entire space of vector fields. Our method parameterizes vector fields via the directional derivatives of scalar functions. This requires the construction of latent inner product, gradient, and divergence operators. In comparison to state-of-the-art orthogonal RNNs, our approach achieves comparable or better results on a variety of benchmark tasks.